23 Функция Гамильтона и канонические уравнения Гамильтона

Рассмотренные ранее уравнения движения (Ньютона и Лагранжа) относятся к дифференциальным уравнениям второго порядка. Из математики известно, что любую систему s дифференциальных уравнений второго порядка можно заменить равносильной системой 2s уравнений первого порядка. Уравнения движения механической системы, записанные в форме дифференциальных уравнений первого порядка, называют каноническими уравнениями движения.

До сих пор рассматривался формализм Лагранжа – составление дифференциальных уравнений движения с помощью функции Лагранжа. В методе Лагранжа независимыми переменными считаются обобщенные координаты и времяt. Обобщенные скорости также входят в лагранжиан и уравнения движения, но считаются зависимыми. В этом методе для описания движения системы вводится понятие об ее траекториях в пространстве конфигураций – s-мерном пространстве обобщенных координат. Такое описание имеет некоторые недостатки: задание точки в s-мерном пространстве дает s начальных условий, а для решения системы s дифференциальных уравнений второго порядка нужно еще s условий. Другими словами, через любую точку конфигурационного пространства проходит бесчисленное множество траекторий системы.

Естественно считать независимыми переменными также и обобщенные скорости (или обобщенные импульсы). Именно так и поступают в методе, предложенном Гамильтоном. Метод составления дифференциальных урав-нений движения для механических и других систем, основанный на использовании функции Гамильтона, называют формализмом Гамильтона.

Функция Гамильтона (обобщенная энергия) определяется выражением:

. (7.1.1)

Поскольку , то в (7.1.1) и.

По определению обобщенный импульс . Считая независимыми переменными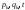(при этом), перепишем выражение для функции Гамильтона в виде:

. (7.1.2)

Здесь p_k и q_k (k = 1, 2, ..., s) – канонические переменные.

Находя полный дифференциал от левой и правой частей (7.1.2), получим (подробнее см. в [5, с. 386]) канонические уравнения Гамильтона для обобщенно-потенциальных сил:,, (7.1.3)

и при наличии диссипативных сил:,, (7.1.4) Поскольку, то уравнения Лагранжа и Гамильтона имеют общие циклические координаты, для которых,. Если все координаты циклические, тоH = const, и все кинематические уравнения движения имеют вид: .

Несложно убедиться, что в общем случае функция Гамильтона изменяется по закону:

, (7.1.5)

из которого следует соответствующий закон сохранения: H = const при и.

В ряде случаев может оказаться полезной при переходе к новым переменным замена на обобщенные импульсы лишь части обобщенных скоростей. Тогда получают уравнения Рауса – уравнения движения, которые относительно одной части переменных имеют вид уравнений Лагранжа, а относительно другой части переменных – вид уравнений Гамильтона. Для переменных вводитсяфункция Рауса:

(7.1.6)

Тогда по аналогии с выводом уравнений Гамильтона, несложно получить уравнения Рауса для обобщенно-потенциальных сил (подробнее см. в [2, с. 172]):

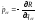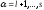,(), (7.1.7)

(k = 1,...,l). (7.1.8)

Отметим, что если все координаты циклические и силы обобщенно-потенциальные, то, а импульсыпостоянные. В этом случае задача нахождения закона движения сводится к решению уравнений Лагранжа относительно координат.