
- •2 Преобразования кинематических характеристик частицы при
- •3 Динамические характеристики частицы. Законы Ньютона
- •4 Принцип относительности Галилея. Механическая концепция
- •5 Уравнение движения частицы относительно исо. Принцип
- •6 Уравнение движения частицы относительно нисо. Силы
- •7 Принципы д¢Аламбера, виртуальных перемещений и
- •8 Обобщенные координаты и обобщенные силы
- •9 Уравнения Лагранжа (второго рода)
- •10 Принцип экстремального действия. Преимущество
- •11 Обобщенная энергия, обобщенный импульс и законы их
- •12 Центр инерции и законы сохранения импульса и момента
- •13 Связь законов сохранения со свойствами симметрии
- •14 Задача двух тел. Движение в центральном поле
- •15 . Задача Кеплера
- •16 Рассеяние частиц. Формула Резерфорда
- •17 Свободные и вынужденные одномерные колебания
- •18 Затухающие колебания
- •19 Вынужденные колебания при наличии трения
- •20 Кинематическое описание твердого тела. Углы Эйлера
- •21 Кинетическая энергия и момент импульса твердого тела
- •22 Уравнения движения твердого тела. Динамические уравнения Эйлера
- •23 Функция Гамильтона и канонические уравнения Гамильтона
- •24 Уравнение Гамильтона-Якоби. Теорема Якоби
- •25 Тензоры деформации и скоростей деформации
- •26 Закон сохранения массы и уравнение непрерывности
- •27 Поле скоростей и его характеристики
- •28 Силы, действующие в сплошных средах. Тензор напряжения
- •29 Необходимые уравнения движения сплошных сред
- •30 Уравнения движения идеальной жидкости
- •31 Интегралы уравнений движения идеальной жидкости
- •32 Звуковые волны
15 . Задача Кеплера
Частный случай
задачи о движении частицы в центральном
поле – задача о движении в поле притяжения
кулоновского типа (например, задача о
движении в поле тяготения). В этом случае
 ,
где
,
где .
Найдем траекторию частицы массой
.
Найдем траекторию частицы массой в таком поле в дифференциальной и
интегральной формах.
в таком поле в дифференциальной и
интегральной формах.
Известно, что в рассматриваемом случае
 (4.3.1)
(4.3.1)
Тогда функцию
Лагранжа
 можно представить в виде:
можно представить в виде: (4.3.2)
(4.3.2)
т. е. рассматривается
движение частицы с обобщенной координатой
 и обобщенной скоростью
и обобщенной скоростью в поле с потенциалом
в поле с потенциалом .
Подставляя (4.3.2) в уравнение Лагранжа,
получаем:
.
Подставляя (4.3.2) в уравнение Лагранжа,
получаем:
 (4.3.3)
(4.3.3)
Заметим, что (4.3.3)
можно получить и непосредственным
дифференцированием механической
энергии
 по времени (учитывая, что
по времени (учитывая, что ).
Учтем далее, что
).
Учтем далее, что и
и (4.3.4)
(4.3.4)
Тогда из (4.3.3) находим:
 (4.3.5) или
(4.3.5) или
 (4.3.6)
(4.3.6)
где
 – проекция силы
– проекция силы на направление
на направление .
Обозначим
.
Обозначим .
При этом
.
При этом и
и
 (4.3.7)
(4.3.7) (4.3.8)
(4.3.8)
Это формула
Бине –
дифференциальной уравнение траектории
при заданной силе. Если
 ,
то
,
то
 (4.3.9)
(4.3.9)
знак
 показывает, что это сила притяжения.
Дифференциальное уравнение траектории
в поле притяжения кулоновского типа:
показывает, что это сила притяжения.
Дифференциальное уравнение траектории
в поле притяжения кулоновского типа:
 (4.3.10)
(4.3.10)
Постоянная
 зависит от масс (зарядов) тел и выбора
системы единиц.
зависит от масс (зарядов) тел и выбора
системы единиц.
Учитывая, что
 (4.3.11)
(4.3.11)
где
 – удвоенная секториальная скорость,
для любого поля притяжения кулоновского
типа имеем:
– удвоенная секториальная скорость,
для любого поля притяжения кулоновского
типа имеем:
 (4.3.12)
(4.3.12)
В частности, для поля тяготения
 (4.3.13)
(4.3.13)
где
 – гауссова постоянная,
– гауссова постоянная, – постоянная тяготения,
– постоянная тяготения, – масса тела, в поле тяготения которого
движется частица массой
– масса тела, в поле тяготения которого
движется частица массой (тело
(тело неподвижно).
неподвижно).
Для описания
движения двух тел с массами
 и
и в системе их центра инерции используют
понятие изображающей точки с массой
в системе их центра инерции используют
понятие изображающей точки с массой ,
расстояние которой от центра инерции
,
расстояние которой от центра инерции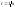 .
Уравнение траектории этой точки
.
Уравнение траектории этой точки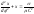 (4.3.14) или
(4.3.14) или (4.3.15)
(4.3.15)
Это неоднородное дифференциальное уравнение второго порядка, общее решение которого
 (4.3.16)
(4.3.16)
где
 и
и – произвольные постоянные,
– произвольные постоянные,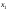 – общее решение соответствующего
(4.3.15) однородного уравнения,
– общее решение соответствующего
(4.3.15) однородного уравнения, – частное решение (4.3.15). Тогда
– частное решение (4.3.15). Тогда (4.3.17)
(4.3.17)
В полярных координатах уравнение конического сечения
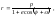 (4.3.18)
(4.3.18)
где
 – параметр кривой,
– параметр кривой, – эксцентриситет. Итак, в поле тяготения
(в поле притяжения кулоновского типа)
частица (или изображающая точка для
замкнутой системы двух частиц) движется
по траектории, представляющей собой
одно из конических сечений. В нашем
случае
– эксцентриситет. Итак, в поле тяготения
(в поле притяжения кулоновского типа)
частица (или изображающая точка для
замкнутой системы двух частиц) движется
по траектории, представляющей собой
одно из конических сечений. В нашем
случае
 (4.3.19)
(4.3.19)
Вид траектории
определяют константы
 и
и ,
причем
,
причем ,
а полная энергия
,
а полная энергия определяет величину
определяет величину .
.
Заметим, что
интегральное уравнение траектории
можно легко получить из (4.3.18), подставляя
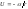 и интегрируя:
и интегрируя:
 (4.3.20)
(4.3.20)
Если
 ,
то
,
то
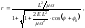 (4.3.21)
(4.3.21)
что при
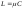 ,
, ,
, совпадает с (4.3.17); при этом
совпадает с (4.3.17); при этом
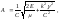 (4.3.22)
(4.3.22)
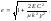 (4.3.23)
(4.3.23)
Постоянная
 задает положение траектории на плоскости;
при
задает положение траектории на плоскости;
при точка с
точка с – ближайшая к полюсу (перигелий
орбиты).
– ближайшая к полюсу (перигелий
орбиты).
При
 эксцентриситет
эксцентриситет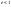 ,
траектория – эллипс; если его полуоси
,
траектория – эллипс; если его полуоси и
и ,
то параметр
,
то параметр ,
площадь
,
площадь ,
секториальная скорость
,
секториальная скорость ,
где
,
где – период (время одного полного оборота
частицы). Точки
– период (время одного полного оборота
частицы). Точки и
и – соответственноперигелий
и афелий
(для спутника Земли – перигей
и апогей).
– соответственноперигелий
и афелий
(для спутника Земли – перигей
и апогей).
Используя известные формулы аналитической геометрии, выразим полуоси эллипса:
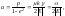 (4.3.24)
(4.3.24)
 (4.3.25)
(4.3.25)
Наименьшее и наибольшее расстояния от центра поля (фокуса эллипса):
 (4.3.26)
(4.3.26)
Зная
 ,
вычислить
,
вычислить и
и можно легко (эти величины могут быть
найдены также как корни уравнения
можно легко (эти величины могут быть
найдены также как корни уравнения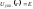 ).
Период движения изображающей точки по
эллипсу определяется энергией:
).
Период движения изображающей точки по
эллипсу определяется энергией:
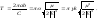 (4.3.27)
(4.3.27)
В частном случае
движения по окружности
 .
.
При
 движение инфинитное (
движение инфинитное ( – парабола,
– парабола, – гипербола). Гиперболической траектории
соответствует энергия
– гипербола). Гиперболической траектории
соответствует энергия .
При этом расстояние перигелия от центра
поля
.
При этом расстояние перигелия от центра
поля
 ,
(4.3.28)
,
(4.3.28)
где «полуось»
орбиты .
(4.3.29)
.
(4.3.29)
Для параболической
траектории
 ,
, и
и
 (4.3.30)
(4.3.30)
Последний случай может осуществляться, если частица (изображающая точка) начинает движение из состояния покоя на бесконечности.
Вычислим теперь скорость движения изображающей точки в разных местах траектории (конического сечения). В полярных координатах
 .
(4.3.31)
.
(4.3.31)
Учитывая, что
 ,
, ,
находим:
,
находим:
 .
(4.3.32)
.
(4.3.32)
Используя уравнение
 для
для ,
получаем:
,
получаем:
 .
(4.3.33)
.
(4.3.33)
Для эллипса
 .
Исследуя на экстремум выражение
.
Исследуя на экстремум выражение
 ,
(4.3.34)
,
(4.3.34)
находим:
 при
при ,
(4.3.35)
,
(4.3.35)
 при
при
 .
(4.3.35)
.
(4.3.35)
Для параболы
 ,
,
 ,
(4.3.36)
,
(4.3.36)
 при
при
 ,
(4.3.37)
,
(4.3.37)
 при
при
 .
(4.3.38)
.
(4.3.38)
Для гиперболы
 ,
при этом и в случае
,
при этом и в случае
 .
.
