26 Закон сохранения массы и уравнение непрерывности

Важная характеристика сплошной среды – ее плотность. Выделим в среде малый объем , охватывающий точку, в которой ищется плотность. Если его масса, то плотность

. (8.4.1)

Это определение имеет смысл только для сплошной среды. Последнее накладывает ограничения на перемещения и плотности точек среды, а в случае конечных перемещений - на скорости точек среды.

Используя переменные Лагранжа, запишем условие того, что выделенный объем V сплошной среды в начальный момент и в конечный моментимеет одинаковую массу:

, (8.4.2) где ,,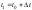. Заменяя во втором интеграле переменные Эйлера переменными Лагранжа, получим:

. (8.4.3) Здесь

(8.4.4)

Для малых перемещений

, (8.4.5)

и из (8.4.2) и (8.4.3) следует:

, (8.4.6)

и, поскольку выбранный объем произволен, то

(8.4.7 )или

. (8.4.8)

Это уравнение непрерывности в переменных Лагранжа или переменных Эйлера.

Собственно, уравнение непрерывности в переменных Лагранжа – (8.4.7). Равенство (8.4.8) представляет собой выражение для относительного объемного расширения 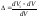при деформации (при неизменной массе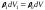и). Из (8.4.8) вытекает:

. (8.4.9)

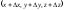Это равенство связывает плотность в двух точках пространства и, которые точка сплошной среды занимает в моменты времениt и 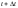, смещаясь на малый вектор.

Разделив последнее равенство на и переходя к пределу при, получимзакон сохранения массы (условие неизменности массы выделенного в среде объема; см. подробнее в [1, с. 29]):

. (8.4.10)

Уравнение непрерывности в переменных Эйлера:

. (8.4.11)

27 Поле скоростей и его характеристики

В части пространства, занятой деформируемой средой, в каждый момент времени в каждой точке можно построить вектор скорости. Совокупность этих векторов образует поле скоростей. В общем случае

; (8.5.1)в случае стационарного поля

. (8.5.2)

Линия тока – линия, в каждой точке которой касательная совпадает с вектором скорости. Касательная к линии тока составляет с осями координат углы, косинусы которых . Скорость составляет с осями координат углы, косинусы которых. Тогда дифференциальные уравнения линий тока можно представить в виде:

. (8.5.3)

Это семейство линий тока. Здесь – элемент дуги линии тока, - его проекции на координатные оси,t играет роль параметра.

Если поле скоростей стационарное, то линии тока не меняются с течением времени и представляют собой траектории движения частиц сплошной среды. Уравнения семейства линий тока в этом случае:

. (8.5.4)

Отметим, что в общем случае линии тока и траектории частиц сплошной среды не совпадают.

Поток скорости – объем сплошной среды, протекающий через некоторую неподвижную поверхность в единицу времени:

, (8.5.5)где – вектор, перпендикулярный к площади в данной точке,– скорость, – ее проекция на . Если поверхностьзамкнута, то– внешняя нормаль к поверхности. Условно полагается, что объем вытекающей среды положительный, а втекающей – отрицательный.

На основании теоремы Гаусса для замкнутой поверхности

. (8.5.6)Аналогично поток массы для замкнутой поверхности. (8.5.7)

Если среда несжимаема или течение стационарно, то из уравнения непрерывности следует, что последний интеграл равен нулю.

Понятие потока массы позволяет получить уравнение непрерывности: поток массы сквозь неподвижную замкнутую поверхность определяет вытекающую в единицу времени массу сплошной среды. Это влечет уменьшение плотности внутри поверхности за единицу времени на и соответствующее уменьшение массы на. Следовательно,. (8.5.8)

Учитывая, что объем произволен, из (8.5.8) имеем:. (8.5.9) Другая существенная характеристика поля скоростей– циркуляция скорости:. (8.5.10)

Здесь интеграл берется по замкнутой кривой L с заданным направлением; – элемент кривой. По теореме Стокса,

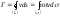, (8.5.11)

т. е. циркуляция скорости равна потоку завихрения сквозь любую поверхность, ограниченную контуром L. По смыслу

(8.5.12)

является вектором завихренности движения (вектором вихря скорости).

Введенное понятие завихренности поля скоростей позволяет разделить движения сплошных сред на два класса: 1) движения безвихревые (потенциальные), для которых (это необходимое и достаточное условие того, что, где– потенциал скорости); 2) завихренные движения, для которых .

Рассмотрим завихренные движения. Пусть точки, в которых , сплошным образом заполняют некоторый объем. В этом случае можно говорить, что поле скоростей порождает поле завихренности, т. к. каждой точке пространства соответствует вектор. Для поля завихренности введем понятиевихревой линии, касательные к которой в любой точке совпадают с вектором в данной точке. Дифференциальные уравнения вихревых линий:

. (8.5.13)

Поскольку , то поток завихренности через замкнутую поверхность равен нулю. В самом деле, по теореме Гаусса

. (8.5.14)

Интенсивность вихря (вихревой трубки) – величина , где– нормальная к сечению трубки тока составляющая вектора. При этом выполняетсяпервая теорема Гельмгольца: интенсивность вихря остается постоянной вдоль вихревой линии. Это означает, что вихревые трубки не прерываются, а либо замкнутые, либо заканчиваются на границе среды. При этом интенсивность вихревой трубки равна циркуляции скорости по любому контуру, расположенному на вихревой трубке и охватывающему последнюю.