21 Кинетическая энергия и момент импульса твердого тела

Рассмотрим сначала твердое тело как дискретную систему материальных точек. Кинетическая энергия такого тела

. (6.3.1)

Учитывая, что (см. (6.1.3)), находим:

. (6.3.2)

Скорости иодинаковы для всех точек твердого тела (удобно считать, что– скорость центра инерции);– масса тела. Тогда второе слагаемое (6.3.2)

(6.3.3)

при условии, что – радиус-вектор-й точки тела относительно центра инерции. Третье слагаемое (6.3.2)

. (6.3.4)

Таким образом, кинетическая энергия тела слагается из кинетической энергии поступательного движения со скоростью центра инерции и кинетической энергии вращательного движения с угловой скоростьювокруг оси, проходящей через центр инерции:

. (6.3.5)

(6.3.5) соответствует теореме Кёнига.

Рассматривая твердое тело как сплошное, запишем (см. рисунок 6.3.1):

. (6.3.6)

Рисунок 6.3.1

(6.3.6) можно использовать для вычислений, если не изменяет направления (например, при вращении вокруг неподвижной оси). Если это условие не выполняется, то.

Учитывая, что=

(6.3.7) и

,,, (6.3.8)

получаем:

, (6.3.9)

где – главные моменты инерции тела;– проекции угловой скорости на оси подвижной (связанной с телом) СК.

Для тела с неподвижной осью вращения или для шарового волчка

. (6.3.10)

Для системы частиц теорема об изменении кинетической энергии записывается в виде:

. (6.3.11)

Для твердого тела и

(6.3.12)

Найдем элементарную работу сил, приложенных к твердому телу при его бесконечно малом перемещении. Пусть на тело действует система сил , точки приложения которых в неподвижной СК определяются радиус-векторами. Элементарное перемещение точки приложения-й силы равно:

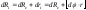. (6.3.13)

Учитывая, что , для всех сил получаем:

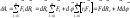, (6.3.14)

где – главный вектор внешних сил,– главный момент внешних сил. При этом

(6.3.15)

Момент импульса твердого тела

. 6.3.16)

Здесь учтено, что . В системе центра инерции

(6.3.17)

Проецируя (6.3.17) на координатные оси, получаем:

(6.3.18)

Если при этом оси СК совпадают с главными осями инерции тела, то

, ,, (6.3.19)

и кинетическая энергия вращательного движения

. (6.3.20)

Из (6.3.19) следует, что в общем случае направления ине совпадают. Совпадение имеет место, если мгновенной осью вращения служит главная ось инерции.

22 Уравнения движения твердого тела. Динамические уравнения Эйлера

Теорема об изменении момента импульса твердого тела (уравнение моментов) может быть записана в виде. (6.4.1)

При проецировании на оси подвижной СК, связанной с центром инерции, в общем случае имеем:. (6.4.2)

В самом деле, при постоянном имеем, а проекцияна неподвижную ось меняется с течением времени, т. е.. Поэтому придадим уравнению моментов форму, удобную для проецирования. Производнаяопределяет скорость конца вектора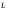; обозначим ее. Тогда. (6.4.3)

Это запись теоремы Резаля: скорость движения конца вектора момента импульса твердого тела по величине и направлению совпадает с вектором главного момента внешних сил, приложенных к телу. В общем случае

, (6.4.4) где

, (6.4.5)

. (6.4.6)

Тогда, (6.4.7)

и теорема об изменении импульса:. (6.4.8)

Проецируя эти уравнения на оси подвижной СК, получим дифференциальные уравнения вращательного движения твердого тела.

Если в качестве осей подвижной СК выбрать главные оси инерции, а начало СК (полюс) совместить с центром инерции, то

(6.4.9)

Учитывая, что,,, 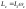получаемдинамические уравнения Эйлера

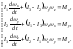(6.4.10)

К решению этих уравнений сводится задача о вращении тела вокруг неподвижной точки. В общем случае это очень сложная задача.

Возможности применения динамических уравнений Эйлера можно показать на примере задачи Эйлера – задачи о свободном вращении симметричного волчка, для которого

, . (6.4.11)

В этом случае система уравнений (6.4.10) существенно упрощается:

(6.4.12)

Решая эту систему при условии совмещения сохраняющегося вектора момента импульса с осьюнеподвижной СК, получим следующие кинематические уравнения движения (см. подробнее в [4, с. 159–160]):

, ,, (6.4.13)

где ,,– углы Эйлера;и– постоянные в данном случае угловые скорости собственного вращения и прецессии;,,– постоянные интегрирования. Закон движения (6.4.13) соответствует так называемойрегулярной прецессии – простейшему движению тела вокруг неподвижной точки.

Можно показать (см. подробнее в [4, с. 160–161]), что если к симметричному волчку приложены моменты сил

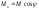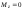, ,, (6.4.14) где, (6.4.15)

то также будет иметь место регулярная прецессия (,,).