В.Н. Дурова М.И. Зайцева О.А. Соколова

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Учебное пособие

Воронеж 2012

ФГБОУ ВПО

«Воронежский государственный технический университет»

В.Н.Дурова М.И. Зайцева О.А. Соколова

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2012

УДК 517.2

Дурова В.Н. Элементы математического анализа: учеб. пособие / В.Н Дурова, М.И. Зайцева, О.А. Соколова. – Воронеж: ФГБОУ ВПО «Воронежский государственный технический университет», 2012. – 228 с.

В учебном пособии излагаются элементы математического анализа. Теоретический материал иллюстрируется большим количеством примеров. Содержатся вопросы для самопроверки, задачи для самостоятельного решения.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего профессионального образования по направлению подготовки бакалавров 080100 «Экономика», профилю «Экономика предприятий и организаций», дисциплине «Математический анализ».

Учебное пособие подготовлено в электронном виде в текстовом редакторе PDF и содержится в файле “МатАн Э.pdf”.

Ил. 67. Табл. 5. Библиогр.: 6 назв.

Рецензенты: кафедра естественно–научных дисциплин Международного института компьютерных технологий (г. Воронеж) ( зав. кафедрой д-р. физ.-мат. наук, проф. В.И. Митрохин); канд. физ.-мат. наук, доц. В.И. Кузнецова

Дурова В.Н., Зайцева М.И., Соколова О.А., 2012

Оформление. ФГБОУ ВПО «Воронежский государственный технический университет», 2012

ВВЕДЕНИЕ

Экономика как наука об объективных причинах функционирования и развития общества еще со времен Адама Смита пользуется разнообразными количественными характеристиками, а потому вобрала в себя большое число математических дисциплин. Сегодня на первый план выступает математическая модель как инструмент исследования и прогноза экономических явлений.

Математические модели представляют собой основу компьютерного моделирования и обработки информации. Они способствуют развитию наших представлений о закономерностях экономических процессов.

Активно использовать математический аппарат возможно только овладев необходимыми знаниями. Кроме того, изучение математических дисциплин позволит будущему специалисту сформировать необходимые компоненты мышления: уровень, кругозор и культуру, которые понадобятся ему для успешной работы и ориентации в будущей профессиональной деятельности.

Данное пособие посвящено изучению следующих разделов высшей математики: начала математического анализа, дифференциальное и интегральное исчисление функции одной и нескольких переменных. Показано, как изучаемый материал применяется при решении экономических задач.

Пособие имеет следующую структуру. В начале каждого параграфа приводятся соответствующие теоретические сведения (определения основных понятий, уравнения, формулы, правила, признаки, методы). Затем следуют вопросы для самопроверки и примеры решения типовых задач различной степени трудности. Далее предлагаются задачи для самостоятельного решения. Ко всем задачам даны ответы.

Пособие рекомендовано студентам бакалавриата направления «Экономика» в помощь к изучению курса «Математический анализ».

3

1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1.1. Функции одной переменной

1.1.1. Понятие функции

Пусть X и Y – некоторые числовые множества и пусть каждому элементу x X по какомулибо закону f поставлен в соответствие один элемент y Y . Тогда будем говорить, что определена функциональная зависимость y от x по закону y f x . При этом x называют независимой переменной (или

аргументом), y – зависимой переменной, множество X - обла-

стью определения (существования) функции, множество Y – областью значения (изменения) функции. Совокупность точек координатной плоскости Oxy, удовлетворяющих уравнению y f x , называется графиком этой функции.

Для обозначения функции и независимой переменной могут быть использованы и другие буквы. Примерами записи функций: y y x , y F x , y g x .

1.1.2. Способы задания функций

Задать функцию – значит указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие (вычисляется) значение зависимой переменной из области значений функции. Существует три основных способа задания функций: табличный, ана-

литический и графический.

Табличный способ. Этот способ имеет широкое применение в разных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т.п. Как правило, в таких таблицах по крайней мере одну из переменных можно принять за независимую (например, время), тогда другие величины будут функциями от этого аргумента.

4

По сути дела, базы данных основаны на табличном способе задания, хранения и обработки информации, а значит, и на табличной форме функциональной зависимости.

Аналитический способ. Этот способ состоит в задании связи между аргументом и функцией в виде формул. Следует подчеркнуть, что функция может определяться и набором формул: разным участкам области определения функции соответствуют разные формулы.

Графический способ. Здесь соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях с употреблением самопищущих приборов (осциллографы, сейсмографы и т.п.).

1.1.3. Область определения функции

Остановимся особо на процедуре нахождения области определения функции.

1. В том случае, когда функция задана аналитически (посредством формулы) y f x и никаких ограничений или ого-

ворок более не имеется. Область ее определения находится только по соблюдению законности выполнения математических операций, входящих в формулу f. Эти ограничения хорошо известны: подкоренное выражение в корне четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком логарифма должно быть только положительным, а также некоторые другие.

ходится из условия x2 5x 6 0. Поскольку x=2 и x=3 – корни квадратного трехчлена , стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интерва-

лах: ,2 и 3, .

5

1.1.4. Классификация функций

Простейшими элементарными функциями называются:

постоянная функция y=const, степенная функция x ( - лю-

функции arcsin x, arccos x, arctgx, arcctgx.

Функции, которые можно получить при помощи конечного числа арифметических операций над простейшими элементарными функциями, а также их суперпозицией (наложе-

нием), образуют класс элементарных функций.

Примеры элементарных функций:

f x x 1 x3 , f x log 2 sin x e x , f x arctg3x.

В свою очередь, элементарные функции классифициру-

ются следующим образом: 1. Функция вида

P x a0 xn a1xn 1 a2 xn 2 an 1x an ,

где n 0 - целое число, a0 0, a1, a2 , , an - любые числа (ко-

эффициенты), называется целой рациональной функцией, или алгебраическим многочленом степени n. Многочлен первой степени называется линейной функцией (поскольку его график изображается прямой линией).

2. Отношение двух целых рациональных функций

R x a0 xn a1xn 1 an 1x an b0 xm b1xm 1 bm 1x bm

называется дробно – рациональной функцией.

Целые и дробно – рациональные функции образуют класс рациональных функций.

6

3. Функция, полученная путем конечного числа суперпозиций и арифметических действий над степенными функциями с целыми и дробными показателями и не являющаяся рацио-

нальной, называется иррациональной функцией.

Примеры иррациональных функций:

fx x2 x, f x x3 4 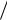x x 1 , f x x32 x1 3.

4.Всякая функция, не являющаяся рациональной или ир-

рациональной, называется трансцендентной функцией.

Примеры трансцендентных функций:

fx cos 2x, f x tgx 3x2 , f x ex 5x.

5. Введем понятие сложной функции (функции от функции). Если у является функцией от переменной u, а u в свою очередь зависит от переменной х, то у также зависит от х.

Пусть y= F(u) и u= (x). Тогда функция у от х y= F[ (x)] – сложная функция.

Примеры сложных функций:

1.2. Приложения функций в экономике

Приведем примеры использования функций из области экономики.

1.2.1. Кривые спроса и предложения. Точка равновесия

Рассмотрим зависимости спроса D (demand) и предложения S (supply) от цены на товар P (price). Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от P имеет вид ниспадающей кривой (рис. 1, а):

7

где a<0. В свою очередь, предложение растет с увеличением цены на товар, и потому зависимость S от P имеет следующую характерную форму:

где b 1 (рис. 1, б). В формулах (1.1) и (1.2) c и d – так называемые экзогенные величины; они зависят от ряда причин (благосостояние общества, политическая обстановка и т.п.). Вполне понятно, что переменные, входящие в формулы (1.1) и

Рис. 1 (1.2), положительны, поэтому графики функций имеют смысл только в первой координатной четверти.

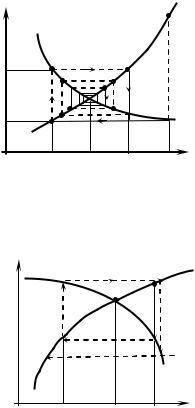
Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению; это условие задается уравнением

(1.3)

и соответствует точке пересечения кривых D и S – это так называемая точка равновесия (точка M на рис. 2). Цена P0 , при

которой выполняется условие (1.3), называется равновесной. При увеличении благосостояния населения, что соответ-

ствует росту величины c в формуле (1.1), точка равновесия M смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предложение S.

8

1.2.2. Паутинная модель рынка

Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проблем рынка, означающая фактический торг между производителем и покупателем.

Пусть сначала цену P1 называет производитель (в простейшей схеме он же и продавец). Цена P1 на самом деле выше

равновесной (естественно, всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спрос D1 при этой цене, находит его низким и

называет свою цену P2 , при которой спрос D1 равен предложению. Цена P2 ниже равновесной (всякий покупатель стремится купить подешевле). В свою очередь производитель оценивает спрос D2 , соответствующий цене P2 , и определяет свою цену P3 , при которой спрос равен предложению, эта цена

выше равновесной (рис. 3, а). Процесс торга в итоге приводит к приближению к равновесной цене, т.е. к «скручиванию» спирали. Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену P0 .

9

Однако спираль установления равновесной цены не всег-

a)

S

D2

D1

б)

D, S

D S

0

P2 P0 P1 P

Рис. 3

да «скручивается» к точке P0 . Если экономика «больна», то

кривые спроса и предложения могут иметь другой вид, нежели кривые, описываемые формулами (1.2) и (1.3). Например, пусть предложение явно недостаточно и в формуле (1.3) b<1,

т.е. S P P 1m d, m 1, а покупательная способность насе-

10