
- •1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1.1.1. Понятие функции
- •1.1.2. Способы задания функций
- •1.1.4. Классификация функций
- •2.1. Предел функции
- •2.2. Бесконечно большая и ограниченная функции
- •2.3. Бесконечно малые и их основные свойства
- •Вопросы для самопроверки
- •3.6. Производные элементарных функций
- •Правила дифференцирования
- •Уравнения (3.9) называются параметрическими уравнениями кривой, а t – параметром.
- •Вопросы для самопроверки
- •Замечание 2. Если производная существует не во всех точках внутри [a,b], то утверждение может оказаться неверным, т.е. на отрезке может не оказаться точки в которой производная обращается в нуль. Например:
- •4.2. Теорема Лагранжа
- •Приведем теорему о конечных приращениях.
- •Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •6.1. Предельные показатели в микроэкономике
- •6.2. Максимизация прибыли
- •8.4. Интегрирование с помощью замены переменной
- •Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
- •11.12.5. Оптимизация спроса
- •12.1. Основные понятия и определения
- •Теорема. Если в уравнении
- •Определение. Общим решением дифференциального уравнения первого порядка называется функция
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •11.12.5. Оптимизация спроса…………………………174
- •12.1. Основные понятия и определения…………………177
- •12.11.4. Неоклассическая модель роста……………..214

6.ПРИМЕНЕНИЕ ИССЛЕДОВАНИЯ ФУНКЦИЙ
ВЭКОНОМИКЕ
6.1. Предельные показатели в микроэкономике
Приведем пример двух предельных показателей в микроэкономике – себестоимости и эластичности.
1. Рассмотрим зависимость себестоимости С произведенной продукции от ее объема Q, т.е. функцию C=f(Q). Так называемая предельная себестоимость характеризует себестоимость С прироста продукции Q :
MC |
C . |
(6.1) |
|
Q |
|
В предположении о непрерывной зависимости C от Q
естественно напрашивается замена разностного отношения в выражении (6.1) его пределом:
MC lim |
C |
C (Q). |
(6.2) |
|
Q |
||||
|
||||
Q 0 |
|
|
||
|
|
|
Обычно в приложениях с использованием аппарата математики под предельной себестоимостью понимают именно величину (6.2).
Например, пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой
С 40Q 0,03Q3.
Определим средние и предельные издержки при объеме продукции Q=15 ден. ед.
Функция средних издержек на единицу продукции определяется по формуле C C / Q , или в нашем случае
С 40 0,03Q2 ,
откуда C (15) 40 0,03 225 33,25 ден. ед.
Предельные издержки определяются, согласно выражению (6.2), по формуле
75

С 40 0,09Q2 ,
откуда при Q=15 получаем С (15) 19,75 ден. ед.
Иными словами, при средних издержках на производство единицы продукции в 33,25 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составят 19,75 ден. ед. и не превысят средних издержек.
2. В анализе и прогнозах ценовой политики применяется понятие эластичности спроса. Пусть D=D(P) – функция спроса от цены товара P. Тогда под эластичностью спроса понимается относительное изменение спроса при изменении цены товара на один процент:
E |
D D100% . |
(6.3) |
|
P P100% |
|
Как и в предыдущем случае, при непрерывной зависимости D от P удобно перейти к пределу при P 0 :
E(D) P |
D (P) |
. |
(6.4) |
|
|||
|
D(P) |
|
|
Аналогичное понятие можно ввести и для функции предложения S(P). Напомним, что функция D(P) убывает, а функция S(P) возрастает с ростом P.
Укажем некоторые свойства эластичности спроса. Как следует из формулы (6.4), ее можно выразить так:
E(D) P(ln D(P)) . |
(6.5) |
Из равенства (6.5) следует, что E(D) обладает свойствами логарифма, а значит:
E(D1D2 ) E(D1) E(D2 ), E(D1 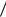 D2 ) E(D1) E(D2 ). (6.6)
D2 ) E(D1) E(D2 ). (6.6)
Заметим, что поскольку функция D(P) убывающая, то D (P) 0, а тогда, согласно формуле (6.4), и E(D)<0.
Различают три вида спроса в зависимости от величины
E(D) :
а) если E(D) 1 (E(D)<-1), то спрос считается эластич-
ным;
76

б) если E(D) 1 (E(D)=-1), то спрос нейтрален; в) если E(D) 1 (E(D)>-1), то спрос неэластичен. Рассмотрим два примера из этой области.
Пример. 6.1. Пусть функция спроса описывается форму-
лой
D(P) D exp(kP2 ), |
(6.7) |
0 |
|
где D0 и k – известные величины. Найти, при каких значениях
цены P спрос будет эластичным.
Согласно формуле (6.4) составляем выражение для E(D):
E(D) 2kPD0 exp( kP2 ) P 2kP2 . D0 exp(kP2 )
Для того чтобы спрос был эластичным, необходимо, чтобы выполнялось неравенство 2kP2 1, откуда P 1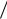

 2k .
2k .
Пример 6.2. Найти изменение выручки с увеличением цены товара при разных вариантах эластичности спроса.
Выручка I равна произведению цены товара P на величину спроса D:
I(P)=D(P) P. |
(6.8) |
Найдем производную этой функции: |
|
I (P) D(P) PD (P). |
(6.9) |
Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (6.4):
а) E(D) <-1. Тогда, подставляя формулу (6.4) в это неравенство, получаем, что правая часть уравнения (6.9) отрицательна. Таким образом, при эластичном спросе повышение цены P ведет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку;
б) E(D)>-1. Из формулы (6.4) следует, что правая часть выражения (6.9) равна нулю, т.е. при нейтральном спросе изменение цены на товар не влияет на выручку;
77
в) E(D)>-1. Тогда I (P) 0, т.е. при неэластичном спросе
повышения цены на товар P приводит к росту выручки. Понятие эластичности распространяется и на другие об-
ласти экономики. Рассмотрим один характерный пример.
Пример 6.3. Пусть зависимость между себестоимостью продукции С и объемом ее производства Q выражается фор-
мулой С=50-0,4Q.
Требуется определить эластичность себестоимости при выпуске продукции Q=30 ден. ед. По формуле (6.4) получаем
E(C) |
0,4Q |
, |
|
|
|||
50 0,4Q |
|||
|
|
откуда при Q=15 искомая эластичность составит около – 0,14, т.е. при данном объеме выпуска продукции увеличение его на 1% приведет к снижению его себестоимости примерно на
0,14%.
6.2. Максимизация прибыли
Пусть Q – количество реализованного товара, R(Q) – функция дохода, C(Q) – функция затрат на производство товара. В реальности вид этих функций зависит, в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара
П(Q)=R(Q)-C(Q). (6.10)
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с выражением (6.2), так что этот принцип можно записать в виде: R (Q) C (Q). Действительно, из необходимого условия
экстремума для функции (6.10) следует, что (Q) 0, откуда и получается основной принцип.
78

Пример 6.4. Пусть |
|
|
||
R(Q) 100Q Q2 , |
C(Q) Q3 |
37Q2 169Q 4000. (6.11) |
||
Тогда |
прибыль |
определяется |
формулой: |
|
(Q) Q3 36Q2 69Q 4000.
Приравнивая производную функции прибыль к нулю, получаем уравнение Q2 24Q 23 0.
Корни этого уравнения Q1 1, Q2 23. Проверка показывает, что максимальная прибыль достигает при Q=23:max 1290.
6.3. Оптимизация налогообложения предприятий
Пусть t – налог с единицы выпускаемой продукции. Тогда общий налог с Q единиц продукции составит T=tQ. В этом случае функция прибыли будет иметь вид
|
(Q) R(Q) C(Q) tQ. |
(6.12) |
|||
Возникает вопрос: каким должен быть налог t,чтобы ве- |
|||||
личина суммарного налога T |
со всей продукции была наи- |
||||
большей? |
|
|
|
|
|
Рассмотрим |
этот |
вопрос |
на примере: |
пусть |
|
R(Q) 16Q Q2 , |
а C(Q) Q2 |
1. |
Тогда функция прибыли |
||
имеет вид (Q) 16Q 2Q2 |
tQ 1. |
|
|
||
Как и в предыдущей задаче, условие максимума прибыли(Q) 0; отсюда получаем значение Q, максимизирующего прибыль с учетом пока еще неизвестного налога t:
Qopt 4 4t .
Полученное значение объема продукции следует подставить в величину суммарного налога T и, в свою очередь, найти условия, при которых величина T будет максимальной. Итак,
79
|
|
t |
|
|
T Qt t 4 |
|
|
;T 0, |
откуда получаем, что t=8. |
|
||||
|
|
4 |
|
|
Отсюда следует, что Qopt 2, и при этом значении максимальная величина прибыли составит max =7, а оптималь-
ный (с точки зрения налогового законодательства) сбор налога
opt 16.
Интересно сопоставить эти цифры с цифрами при отсутствии налогообложения. При t=0 решение задачи на максими-
зацию |
прибыли |
дает |
следующие |
результаты: |
Qopt 4, max 31. |
Следовательно, уменьшение налогооб- |
|||
ложения стимулирует рост выпуска продукции и приводит при этом к увеличению прибыли от ее реализации. Понятно, почему производители прикладывают столько усилий, чтобы снизить ставку налога.
6.4. Закон убывающей эффективности производства
Этот закон утверждает, что при увеличении одного из основных факторов производства, например капитальных затрат K, прирост производства, начиная с некоторого значения K, является убывающей функцией. Иными словами, объем произведенной продукции V как функция от K описывается графиком со сменой выпуклости вниз на выпуклость вверх.
Характерный вид этой функции дается уравнением:
V |
|
V (K ) V lim 1 a e bK c , |
|
|
|
|
|
(6.13) |
|
Vmin |
|
|||
|
|
|||
|
|
|
где a, b и c – известные поло- |
|
|
|
|
жительные числа (они опре- |
|
|
|
|
деляются прежде всего струк- |
|
|
Kcr |
K |
турой организации производ- |
|
|
Рис. 35 |
|
80 |
|
|
|
|
|
|

ства), а V lim - предельно возможный объем выпускаемой про-
дукции. Нетрудно подсчитать, что вторая производная функция (6.13) имеет вид
|
2 |
bK c |
a e bK c 1 |
|
V (K ) V limab |
|
e |
1 a bK c . |
(6.14) |
|
|
|
e |
|
Критическая точка находится по условию V (K) 0, от- |
||||
куда |
|
|
|
|
Kcr c Ina b. |
|
(6.15) |
||
График функции (6.13) приведен на рис. 35. В точке перегиба выпуклость графика функции (6.15) вниз меняется на выпуклость вверх . До этой точки увеличения капитальных затрат приводит к интенсивному росту объема продукции: прирост объема продукции (аналог первой производной) возрастает, т.е. V (K) 0. При K Kcr прирост объема выпускаемой
продукции снижается, т.е. V (K) 0, и эффективность увели-
чения капитальных затрат падает.
Таким образом, в стратегии капиталовложений очень важным моментом оказывается определение критического объема затрат, сверх которого дополнительные затраты будут приводить ко все меньшей отдаче при данной структуре организации производства. Зная этот прогноз, можно пытаться совершенствовать и менять структуру организации производст-
ва: «улучшать» показатели a, b, c и V lim в сторону повышения эффективности капиталовложений.
81

7.КОМПЛЕКСНЫЕ ЧИСЛА
7.1.Определение комплексного числа
Понятие комплексного числа возникло в связи с необходимостью решать квадратные уравнения при любых значениях дискриминанта, в том числе и отрицательных.
При этом возникает необходимость расширения понятия числа, необходимость введения чисел более общей природы. Действительно числа уже будут частным случаем этих «новых» чисел.
Определение. Комплексным числом называется выраже-
ние z =x+iy, где x и y – действительные числа, а i – называют
мнимой единицей: i2= 1.
Числа х и y называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются символами: x = Re z , y = Im z.
Если y = 0, z = x + i0 считается совпадающим с действительным числом x. Если x = 0, то z = 0 + iy обозначается просто iy и называется мнимым числом.
Выберем на плоскости декартову прямоугольную систему координат и будем рассматривать упорядоченную пару чисел (x,y) как координаты точек этой плоскости.
Тогда каждому числу z = x + iy будет отвечать определённая точка z (x,y) плоскости и, наоборот, каждой точке плоскости будет отвечать определённое число z = x + iy.
Таким образом, между множеством комплексных чисел и множеством точек плоскости Оху существует взаимно однозначное соответствие.
у
z(x,у)
r |
|
|
у |
|
|||
0 |
|
x |
|
|
|||
x |
|
||
|
|
||
|
|
|
Рис.36
Плоскость Оху называется плоскостью комплексных чисел. Действительные числа изображаются при этом точками оси Oх.
82

Ось Oх называется действительной осью. Мнимые числа z = iy изображаются точками на оси Oу, которая называется
мнимой осью.
7.2.Две формы записи комплексного числа
1)Алгебраическая форма
z = x + iy. |
(7.1) |
Два комплексных числа z1 = x1 + iy1 и z2 = x2 + iy2 равны друг другу (z1 = z2) тогда и только тогда, когда x1 = x 2, и
y1 = y2. |
|
|
Комплексные числа z |
и |
z называются взаимно сопря- |
жёнными, если z = x + iy, |
z |
= x – i y. |
Точки z(x,y) и z(x,-y) симметричны относительно действительной оси Oх.
2) Тригонометрическая форма
Введём в рассмотрение r - радиус-вектор точки z и угол φ, образованный им с положительным направлением оси Oх.
(рис. 36).
Величины r и φ называются, соответственно, модулем и аргументом комплексного числа z и обозначаются символами: r = | z |; φ = Arg z .
Модуль комплексного числа определяется однозначно
формулой (из треугольника, рис. 36) r = | r | 
 x 2 y 2 .
x 2 y 2 .
Все значения аргумента φ удовлетворяют соотношению tg xy .
Угол φ называется аргументом комплексного числа z:Arg z( Arg z ) .
Аргумент определяется не однозначно, а с точностью до числа, кратного 2π. Если z =0, то аргумент произволен.
Наименьшее по модулю значение аргумента Arg z назы-
вается его главным значением:
83
arg z или 0 2 .
Главное значение аргумента определяется однозначно: |
|
Arg z arg z 2k |
k 0, 1, 2,... . |
Из треугольника: x = | z | cosφ и y = | z | sinφ. Поэтому лю-
бое комплексное число можно записать в тригонометрической форме:
z x iy | z | cos i | z | sin или ( | z | =r), |
|
z r cos i sin . |
(7.2) |
Два комплексных числа z1 и z2 равны тогда и только то-
гда, когда равны их модули, а аргументы равны или отличаются на 2кπ:
|
|
|
|
z1 z2 |
|
z1 |
|
|
|
|
|
z2 |
|
|
|
|
; 1 |
2 2k |
k 0, 1, 2,... . |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Для перехода от алгебраической формы (7.1) к тригоно- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
метрической (7.2) пользуются равенствами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x 2 y 2 ; tg |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
cos |
|
|
; sin |
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
z |
|
|
|
|
|
z |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Примеры 7.1. Записать комплексные числа в тригоно- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
метрическом виде. |
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. z1 1, x 1; y 0; 0 , |
|
|
|
|
|
|
|
|
z2= i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z3= |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
12 02 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
=1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 cos 0 i sin 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 37 |
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
z |
|
i, x 0; y 1; |
|
z |
|
|
|
1, |
,i 1 cos |
2 |
i sin |
. |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
3. |
z3 |
1, |
x 1; y 0; |
|
z |
|
1, |
, 1 1 cos i sin . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
z |
4 |
i, |
x 0; y 1; |
|
z |
|
1, |
2 |
,i 1 cos |
2 |
i sin |
|
2 |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

7.3. Действия над комплексными числами
На множестве комплексных чисел определены те же действия, что и на множестве действительных чисел. Пусть
z1 x1 i y1 и z2 x2 i y2 .
а) Сумма и разность двух комплексных чисел определяется следующим образом:
z1 z2 x1 x2 i y1 y2 ,
т.е. при сложении комплексных чисел их действительные и мнимые части складываются, а при вычитании вычитаются.
б) Произведение двух комплексных чисел получается по
правилу умножения многочленов, учитывая, что i2 = -1: |
|||||
z1 z2 |
x1 i y1 x2 i y2 |
|
|||
x1 x2 y1 y2 i x1 y2 x2 y1 . |
|||||
Если комплексные числа заданы в тригонометрической |
|||||
форме: |
|
||||
|
z1 r1 cos 1 i sin 1 |
, z2 r2 cos 2 i sin 2 , |
|||
z1z2 |
|
||||
r1r2 cos1cos 2 - sin1sin 2 i sin 1 cos 2 cos 1 sin 2 |
|||||
или |
z1 z2 r1r2 cos 1 2 i sin 1 2 . |
||||
Здесь |
|
z1z2 |
|
r1r2 и |
Argz1z2 Argz1 Argz2 . |
|
|
||||
Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей.
в) Деление комплексных чисел вводится как операция, об-
ратная умножению:
z1 z, если zz2 z1 z2 0 z2
В алгебраической форме:
85
|
z1 |
|
|
x1 iy1 |
|
x1 iy1 |
x2 iy2 |
|
; |
|
|
|
|
|
|||||
|
|
|
|
|
x2 iy2 |
x2 iy2 |
|
|
|
|
|
|
|||||||
|
z2 |
|
x2 iy2 |
|
|
|
|
|
|
||||||||||
|
z1 |
|
x1x2 y1 y2 i y1x2 x1 y 2 |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z2 |
|
|
|
|
x 2 y |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Пример 7.2. Вычислить: |
|
|
|
|
|
|
|
|
|
||||||||||
|
3 2i |
|
|
3 2i 4 3i |
12 9i 8i 6 |
|
18 i |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
4 3i |
|
4 3i 4 3i |
|
|
16 9 |
|
|
|
25 |
25 |
||||||||
Пусть числа z1 и z2 заданы в тригонометрической форме. Найдём модуль и аргумент частного. По определению:
z1 zz2 |
|
z1 |
|
|
|
z |
|
|
|
z2 |
|
и Arg z1 |
Arg z Arg z2 . |
||||||||||
|
|
|
|
|
|
||||||||||||||||||
Отсюда: |
|
z |
|
|
|
|
z1 |
|
|
|
и Arg z Arg z |
Arg z |
2 |
. |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
z2 |
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.
z1 |
|
r1 |
cos |
|
|
|
i sin |
|
|
|
. |
|
z2 |
r2 |
1 |
2 |
1 |
2 |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
г) Возведение комплексных чисел в натуральную сте-
пень.
Целая положительная степень комплексного числа опре-
деляется так же, как и действительного: z n z z...z .
n
Например: i 2 1;i 3 i 2i i;i 4 i 3i 1; i5 i4i i и т.д. В общем случае:
i4k 1;i4k 1 i;i4k 2 i;i4k 3 i .
Пусть число z задано в тригонометрической форме: z r cos i sin .
Отсюда: z n r n cos n i sin n . 86

Пример 7.3. Вычислить (1 i 10 . Запишем число z=1+i в
тригонометрическом виде. Здесь |
r |
12 12 = |
|
, |
||||||||
2 |
||||||||||||
tg =1; |
|
|
|
|
|
|
|
i sin |
|
|
||
|
|
|
||||||||||
|
; z = 2 cos |
|
|
, |
||||||||
|
|
4 |
|
|
|
|
4 |
|
4 |
|
||
|
|
|
10 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|||||
1 i |
cos 10 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
i sin |
5 |
|
||
2 |
|
cos |
|
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
i sin 10 |
|
|
||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
i sin |
|
|
32 cos |
. |
||||||
|
|
|
|
2 |
|
2 |
|
д) Извлечение корня.
Корнем n-ой степени из комплексного числа z называется
такое число w (w= n z ), что wn=z.
z ), что wn=z.
Пусть числа z и w представлены в тригонометрической
форме: |
|
|
|
|
|
|
|
|
|
z r cos i sin и w cos i sin . |
|||||||||
Найдём ρ и . Так как |
|
|
|||||||
wn z, n cos n i sin n r cos i sin |
|||||||||
n r , n 2k |
k 0, 1,... . |
||||||||
Поэтому: ρ= n |
|
- арифметическое значение корня из по- |
|||||||
r |
|||||||||
ложительного числа r, а = 2k |
(k= 0, 1, 2,... ). |
||||||||
|
|
|
|
|
|
|
|
n |
|
|
n |
|
n |
|
cos 2 k i sin 2 k . |
||||
w |
z |
r |
|||||||
k |
|
|
|
|
|
n |
|
||
|
|
|
|
|
|
n |
|||
Аргументы к дающие существенно различные корни n- ой степени из z, соответствуют только n значениям k (0,1,2,…n-1). Остальным целым k соответствуют значения k, отличающиеся от одного из указанных на величину, кратную
2π.
87
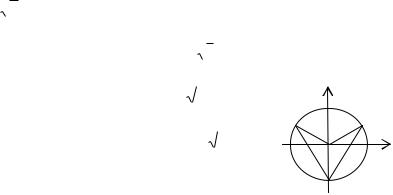
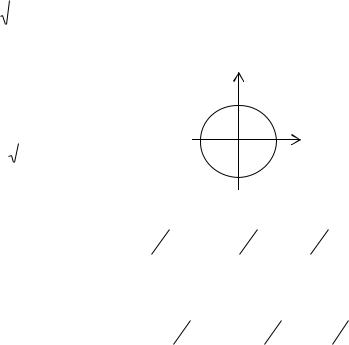
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из этих формул. Из формул вытекает, что все значения корня лежат на окружности радиуса
ρ= n r и делят окружность на n равных частей.
r и делят окружность на n равных частей.
Пример 7.4. Вычислить 3 i . Запишем число в тригонометрической форме:
i . Запишем число в тригонометрической форме:
|
cos i sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|||||||||||
1. k 0, w |
|
|
|
3 |
|
i |
; |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 |
|
|
6 |
|
6 |
|
2 |
2 |
|
|
|
w1 |
|
|
|
|
w0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
||||||||||||||||||
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. k 1, w |
cos |
|
i sin |
|
|
3 |
|
|
i |
; |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
6 |
|
6 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. k 2 , w2 |
cos |
|
3 |
|
i sin |
3 |
|
|
i |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 38
Вопросы для самопроверки
1.Какие числа называются комплексными?
2.Что называется действительной и мнимой частью комплексного числа?
3.Что называется модулем и аргументом комплексного
числа?
4.Какие формы записи комплексных чисел вы знаете?
5.В каком случае два комплексных числа называются сопряженными?
6.По каким правилам производятся действия над комплексными числами?
Задачи для самостоятельного решения
Найти:
1. (3+5 i)(3- i). |
Ответ.17+17 i. |
88

2. |
|
3 i |
. |
|
Ответ. |
7 |
|
|
|
19 |
|
i. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
4 5i |
|
41 |
41 |
|
|
|
|
|
|||||||||
3. (4 7i)3 . |
Ответ. –524+7i. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4. |
|
|
5 12i . |
Ответ. (2 3i). |
|
|
|
|
|||||||||||
Привести к тригонометрическому виду: |
|
|
|
||||||||||||||||
5. |
1+i. |
|
|
|
|
(cos |
i sin ). |
||||||||||||
Ответ. |
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|||||
6. |
1 i. |
|
|
|
(cos |
7 |
i sin |
|
7 |
). |
|||||||||
Ответ. |
|
2 |
|||||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|||||
8.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
8.1.Первообразная. Неопределённый интеграл
Основная задача дифференциального исчисления: по заданной функции ƒ(х) найти её производную ƒ/(x) или дифференциал ƒ/(x)dx. Теперь будем решать обратную задачу: по заданной производной или дифференциалу найти саму функцию
ƒ(х).
Определение 1: Функция F(x) называется первообразной функцией для функции ƒ(х) на интервале (a, b), если F(x) диф-
ференцируема на (a, b) и F/(x)=ƒ(х) или dF(x)=ƒ(x)dx для всех x (a, b) .
Простейшие примеры:
|
x |
3 |
|
|
1 |
|
|
|
1 |
|
|
||
1. f x x2; F x |
|
|
|
x3 |
|
|
3x2 |
|
|||||
|
|
, |
так как |
|
|
|
|
; |
|||||
|
|
|
|
||||||||||
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|||
2. f x cos x; F x sin x, |
так как |
sinx cos x . |
|||||||||||
Если для ƒ(х) существует первообразная F(x), то существует и бесчисленное множество первообразных. Например, для ƒ(х) = х2 первообразными будут функции:
89
1 |
|
x |
3 |
; |
1 |
|
x |
3 |
1; |
1 |
|
x |
3 |
10 |
и т.д. |
3 |
|
3 |
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Теорема 1. Если F(x) есть первообразная для функции ƒ(х) на (a, b), то функция F(х) + C – так же первообразная, где C - любое число.
Теорема 2. Если две функции F(x) и Ф(х) являются первообразными для ƒ(х) на (a,b), то их разность постоянна на этом интервале: Ф(х) – F(x) = C для всех x (a, b) .
Из данных теорем следует, что если F(x) есть первооб-
разная для ƒ(х) на (a, b), то любая другая первообразная Ф(х) для ƒ(х) на (a, b) имеет вид
Ф x F x c . |
(8.1) |
Таким образом, если производные двух функций тождественно равны, то сами функции могут отличаться лишь на постоянное слагаемое.
Определение 2. Если функция F(x) является первообразной для ƒ(х), то выражение F x c называется неопреде-
лённым интегралом функции ƒ(х) и обозначается символом
f (x)dx .
Если F(x) – одна из первообразных для ƒ(х), то по определению:
f x dx F x c |
(8.2) |
Операцию нахождения неопределённого интеграла (первообразной) называют интегрированием функции ƒ(х). Функция, имеющая первообразную, называется интегрируемой.
Все ли функции имеют первообразную? Ответ на этот вопрос дает следующая теорема.
Теорема 3. Если функция ƒ(х) непрерывна на (a, b), то для неё существует первообразная на (a, b), т.е. она интегрируема.
Из определения 2 следует:
90
1. Производная от неопределённого интеграла равна по-
дынтегральной функции (применяется для проверки):
f x dx f x .
2.Дифференциал от неопределённого интеграла равен подынтегральному выражению:
df x dx f x dx .
3.Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
dF(x)=F(x).
8.2.Таблица неопределённых интегралов
Так как интегрирование есть операция обратная дифференцированию, то всякую формулу для производной конкретных функций можно обратить:
F x f x f x dx F x c .
Поэтому таблицу основных интегралов получаем из таблицы производных, записав её справа налево:
1. xadx xa 1 c a 1 . a 1
2. dxx ln x c x 0 .
3. axdx ax c a 0;a 1 . ln a
4. exdx ex c .
91

5.sin xdx cos x c .
6.cos xdx sin x c .
7. |
|
|
dx |
|
|
tgx c . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos2 x |
|
|
|
|
|
|
||||||||||||||||||||
8. |
|
|
|
dx |
|
|
ctgx c . |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
sin2 x |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin x c |
|
|
|
|
|||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 x2 |
|
arccos x |
c |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctgx c |
|
|
|
|
|
|
|||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
2 |
|
|
|
arcctgx |
c |
|
|
||||||||||||||||
11. |
|
|
|
dx |
|
|
|
|
ln |
x |
|
x 2 a 2 |
c . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
2 |
|
a |
2 |
|
|
||||||||||||||||||
12. |
|
|
|
|
|
|
|
|
|
|
a x |
|
|
|
|
|||||||||||
|
|
dx |
|
|
1 |
|
|
c . |
|
|||||||||||||||||
|
|
|
ln |
|
|
|||||||||||||||||||||
|
|
2 |
2 |
2a |
a x |
|
||||||||||||||||||||
|
|
|
|
|
a |
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В таблице производных нет формул, соответствующих формулам 11 и 12. Поэтому в их справедливости убедимся с
помощью дифференцирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2x |
|
|
|
|
|||
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||
x |
|
a |
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
ln |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x |
|
2 |
a |
2 |
|
|
|
|
2 |
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
2 x |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
x 2 a 2 x |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
|
x 2 a 2 |
|
|
x 2 a 2 |
x 2 a 2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
a x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ln |
|
|
|
|
|
|
|
|
ln |
a x |
ln |
a x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2a |
|
a x |
|
|
|
|
2a |
92 |
|
|
|
2a a x |
|
a x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
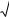
|
1 |
|
a x a x |
|
1 |
. |
|
2a |
a2 x2 |
a2 x2 |
|||||
|
|
|
|
Интегралы, содержащиеся в таблице, называются табличными и их надо твёрдо запомнить, так как вычисление интеграла сводится к последовательным операциям, результатом которых является приведение заданного интеграла к табличному (если это возможно).
8.3. Основные свойства неопределённого интеграла
Теорема 1. Постоянный множитель можно выносить за знак неопределённого интеграла:
Af x dx A f x dx . |
(8.3) |
Теорема 2. Неопределённый интеграл от алгебраической суммы двух или нескольких функций равен сумме неопределённых интегралов от слагаемых:
f x g x dx f x dx g x dx |
(8.4) |
(верно для любого конечного числа слагаемых)
Теорема 3. Если f x dx F x c , то
f ax b dx |
1 |
F ax b c . |
(8.5) |
a |
Для доказательства теорем находят производные левой и правой частей равенств.
|
Примеры 8.1. Вычислить неопределенные интегралы. |
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1. |
x3 x 2 x x 1 |
|
|
|
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
1 x |
|
2 |
x |
2 |
|
x |
2 |
|
dx x |
|
|
dx xdx dx |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
93
