
- •1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1.1.1. Понятие функции
- •1.1.2. Способы задания функций
- •1.1.4. Классификация функций
- •2.1. Предел функции
- •2.2. Бесконечно большая и ограниченная функции
- •2.3. Бесконечно малые и их основные свойства
- •Вопросы для самопроверки
- •3.6. Производные элементарных функций
- •Правила дифференцирования
- •Уравнения (3.9) называются параметрическими уравнениями кривой, а t – параметром.
- •Вопросы для самопроверки
- •Замечание 2. Если производная существует не во всех точках внутри [a,b], то утверждение может оказаться неверным, т.е. на отрезке может не оказаться точки в которой производная обращается в нуль. Например:
- •4.2. Теорема Лагранжа
- •Приведем теорему о конечных приращениях.
- •Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •6.1. Предельные показатели в микроэкономике
- •6.2. Максимизация прибыли
- •8.4. Интегрирование с помощью замены переменной
- •Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
- •11.12.5. Оптимизация спроса
- •12.1. Основные понятия и определения
- •Теорема. Если в уравнении
- •Определение. Общим решением дифференциального уравнения первого порядка называется функция
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •11.12.5. Оптимизация спроса…………………………174
- •12.1. Основные понятия и определения…………………177
- •12.11.4. Неоклассическая модель роста……………..214
11.12.5. Оптимизация спроса
Типичной задачей исследования спроса является оптимизация функции полезности при ограничениях на бюджет покупателя. Рассмотрим такой пример: найти величины спроса x и y на две разновидности товара при ценах на них соответственно a и b, сели потребитель при бюджете К стремится максимизировать функцию полезности, которая имеет вид
F x, y x |
a |
|
b |
|
|
|
y |
|
. |
|
|
a b 1 |
a b 1 |
(11.27) |
|||
Из условия задачи следует, что при покупке, стоимость которой ах +ву, потребитель может израсходовать сумму, не превышающую К. Следовательно, необходимо найти точку (х, у), в которой функция (11.27) достигает максимума при ограничениях:
|
ax by K, |
x 0, y 0 . |
|
|
|
|
(11.28) |
||
Ограничения |
(11.28) |
y |
|
|
|
|
|
|
|
задают на плоскости |
Оху |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
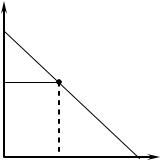
замкнутую область D в виде |
K/b |
K |
|
K |
|
|
|||
треугольника (рис. 63), в ко- |
|
|
|||||||
|
|
|
, |
|
|
|
|||
|
|
|
|
|
|
|
|||
торой следует искать точку |
|
a b |
|
a b |
|||||
максимума функции (11.27). |
|
|
|
|
|
|
|
||
Вычислив |
частные |
F=0 |
|
|
|
|
|
|
|
функции полезности (11.27), |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
находим, что единственная |
|
|
|
|
|
|
|
||
критическая точка (0,0) |
на- |
0 |
|
|
|
|
|
|
|
ходится на границе области |
|
F=0 K/a |
|
x |
|||||
|
|
|
|||||||
D; и в ней, как и на гранич- |
|
|
|
|
|
|
|
||
ных линиях х = 0 и у = 0, |
|
Рис. 63 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
функция F(x,y)=0, |
что явля- |
|
|
|
|
|
|
|
|
ется минимальным ее значением. Следовательно, нужно искать точку максимума этой функции на границе
ax by K,
области D. Подставляя из этого уравнения выражение для у в функцию (11.27), получаем функцию одной переменной
174
f x b |
|
b |
|
a |
|
|
a b 1 x a b 1 (K ax)a b 1 . |
||||||
|
|
|
|
|
|
b |
Критическую точку этой функции найдем из условия обращения в нуль ее первой производной; получаем, что х=К/(а+в),откуда у=К/(а+в). Таким образом, в данной модели оптимальный спрос на оба вида товара одинаков: он пропорционален бюджету и обратно пропорционален суммарной цене товара.
Вопросы для самопроверки
1.Что называется функцией двух переменных, ее областью определения? Дайте геометрическое толкование этих понятий.
2.Что называется пределом функции двух переменных в
точке?
3.Как определяются частные производные? Сформулируйте правила нахождения частных производных функции нескольких переменных.
4.Когда функция z =f (x,у) называется дифференцируемой в данной точке?
5.Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных производных функции двух переменных.
6.Что называется максимумом (минимумом) функции двух переменных? Выведите необходимые и сформулируйте достаточные условия экстремума функции двух переменных.
7.Что называется производной от функции z =f (x,у) в
данной точке М0 по направлению вектора s? Выведите формулу для ее вычисления.
8.Что называется градиентом скалярной функции в данной точке?
175

|
|
|
|
Задачи для самостоятельного решения |
||||||||||||||||
|
1. |
Найти |
|
область |
|
определения |
функции: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z 1 / |
|
1 x 2 y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ответ. Часть плоскости внутри круга x 2 y 2 <1. |
|||||||||||||||||||
|
2. Найти частные производные функции: z |
x 2 |
|
x |
. |
|||||||||||||||
|
y 2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||
|
Ответ. |
z |
|
2x |
|
1 |
; |
z |
|
x |
|
2x 2 |
. |
|
|
|
|
|||
|
x |
y 2 |
y |
y |
y 2 |
y 3 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.Найти полный дифференциал функции z arctg x y .
xy
Ответ. |
dz |
z |
dx |
z |
dy |
xdy ydx |
. |
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
x |
|
y |
|
x 2 |
y 2 |
|
|||||
4. Показать, |
что функция z |
1 |
|
e x2 /(4a2t) |
удовлетворяет |
|||||||||
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|||
уравнению |
z |
a |
2 2 z |
. |
|
|
|
|
|
|
|
|
|
|
t |
x 2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Найти экстремум функции z x 2 xy y 2 |
3x 6 y. |
|||||||||||||
Ответ. В точке М (0,3) функция имеет минимум zmin= 9.
6. Найти наибольшее и наименьшее значения функции z=xy+x+y в квадрате, ограниченном прямыми х=1, х=2, у= 2,
у=3.
Ответ. zнаим =5, zнаиб=11.
8. Найти производную функции z x 2 y 2 в точке М
(1,1) в направлении вектора a, составляющем угол =60 с положительным направление оси Ох.
176

|
z |
|
|
|
||
Ответ. |
1 3. |
|||||
a |
||||||
|
|
|
|
|||
9. Найти |
|
величину и направление градиента функции |
||||
z x 2 y в точке |
М (1,2). |
|||||
Ответ. (grad z)М= 4i +j . grad z M = 
 17 .
17 .
12.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
12.1.Основные понятия и определения
Определение. Дифференциальным уравнением называет-
ся уравнение, связывающее независимую переменную х , искомую функцию у= f(x) и ее производные y , y ,..., y(n) .
Символически дифференциальное уравнение можно записать в виде:
F(x, y, y , y ,..., y (n) ) 0.
Если искомая функция у= f(x) есть функция одной переменной, то уравнение называется обыкновенным.
Определение. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Так, например, уравнение y 2xy 2 7 0 есть уравне-
ние первого порядка.
Определение. Решением или интегралом дифференци-
ального уравнения называется всякая функция у= f(x), которая, будучи подставлена в уравнение, превращает его в тождество.
Дифференциальное уравнение первого порядка имеет вид
(12.1)
Если это уравнение можно разрешить относительно y ,
то его можно записать в виде у = f(x, у). В этом случае говорят что уравнение разрешено относительно производной. Для та-
177
