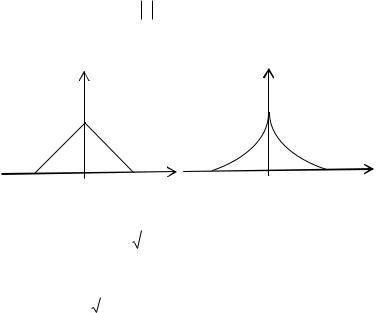
1) функция y 1 x , график которой приведен на ри-

сунке 18 - пример функции, производная которой не обращается в нуль.

[-1,1] и обращается в нуль на концах, а производная внутри

4.2. Теорема Лагранжа

Приведем теорему о конечных приращениях.

Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что

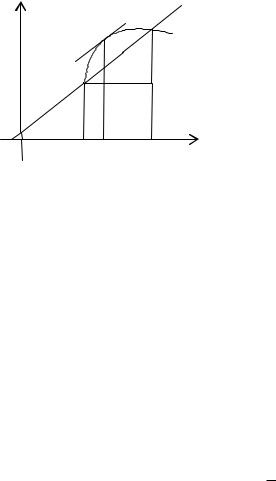
Как и теорема Ролля, теорема Лагранжа имеет простой геометрический смысл. При выполнении условий теоремы на отрезке [a,b] найдется по крайней мере одна точка х, в которой касательная параллельна хорде АВ (рис. 20).

52

f(x)

N

A

Рис. 20

4.3. Теорема об отношении приращений двух функций (теорема Коши)

Теорема Коши. Если f(x), g(x) – две функции непрерывные на отрезке [a,b] и дифференцируемые внутри него, причем g (x) 0 внутри отрезка, то внутри отрезка [a,b] найдется

Геометрический смысл теоремы такой же, как и в случае теоремы Лагранжа.

4.4. Предел отношения двух бесконечно малых величин

(раскрытие неопределенности вида { 00 })

Пусть функции f(x) и g(х) на некотором отрезке [a,b] удовлетворяют условиям теоремы Коши и обращаются в нуль в точке х=а этого отрезка, т.е. f(a)=0, g(a)=0.

Отношение f(x)/g(x) не определено при x=a, но определено во всех точках x a.

53

теорема.

Теорема 1. (Правило Лопиталя). Пусть функции f(x) и g(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Коши и обращаются в 0 в точке x=a , тогда если существует предел отношения

Замечание 1. Правило Лопиталя имеет место и в том случае, если функции f(x) и g(x) не определены при x=a , но

x=a, чтобы они оказались непрерывными f (a) lim f (x) 0 .

x a

Замечание 2. Если f (a) g (a) 0 , и производные f (x), g (x) удовлетворяют условию теоремы (правила Лопи-

54

Пример 4.1.

4.5. Предел отношения двух бесконечно больших величин

(раскрытие неопределенности вида { })

Теорема 2. (Правило Лопиталя). Пусть функции f(x) и g(x) определены и дифференцируемы при всех x a в окрест-