Приведем без вывода несколько эквивалентных бесконечно малых, использование которых сильно упрощает вычисление пределов:

х sin x, x tg x, x arcsin x, x arctg x, x e x 1.

Вопросы для самопроверки

1.Сформулируйте определение предела переменной величины, предела функции при стремлении аргумента к некоторому значению а, и предела функции при стремлении аргумента к бесконечности.

2.Как связаны между собой понятия предела функции с понятиями пределов слева и справа?

3.Дайте определение ограниченной функции.

4.Что такое бесконечно малая величина и каковы ее основные свойства?

5.Какая величина называется бесконечно большой? Какова ее связь с бесконечно малой?

6.Что называют «первым замечательным пределом»?

7.Дайте определение числа е и «второго замечательного предела».

8.Сформулируйте определение непрерывной функции.

9.Сформулируйте основные свойства функций непрерывных на отрезке и дайте геометрическое истолкование этим свойствам.

Задачи для самостоятельного решения

Вычислить пределы функций

3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

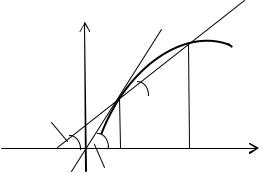
3.1. Задача о касательной к кривой

Дана кривая, на ней точка М. Установим понятие касательной к кривой в точке М.

Общее определение. Зафиксируем на кривой точку М0 и возьмем произвольную точку М1. Проведем секущую М0М1. Если точка М1 перемещается вдоль по кривой неограниченно приближаясь к М0, то секущая будет поворачиваться вокруг М0 (рис. 13).

Рис. 13 Касательной к кривой в точке М0 будем называть пре-

дельное положение секущей, когда точка М1 вдоль по кривой стремится к точке М0.

Рассмотрим функцию f(x) и соответствующую этой функции кривую у= f(x). Пусть при некотором значении х функция имеет значение у, т.е. точка М0 имеет координаты (х,у). Дадим аргументу х приращение х. Тогда функция получит приращение у. Точка М1 будет иметь координаты (х+ х,у+ у). Угловой коэффициент секущей М0М1

Здесь - угол наклона секущей к оси Ох. Если точка М1

Решение представленной задачи свелось к вычислению предела отношения приращения функции к приращению аргумента y=f(x).

3.2. Определение производной и ее геометрический смысл

Предел отношения приращения функции y к, вызвавшему это приращение, приращению аргумента x , при

x 0 , т.е.

называется производной функции f(x) по независимой переменной x.

Обозначается f (x), y , dydx . Операцию нахождения

производной называют дифференцированием.

Из задачи рассмотренной в предыдущем параграфе следует, что угловой коэффициент касательной, проведенной к кривой у =f (x) в некоторой точке, равен значению производной функции в этой точке. В этом и состоит геометрический смысл производной.

35

Пример 3.1. Дана функция y= x 2 , найти ее производную y : 1) в произвольной точке; 2) при х=3.

Решение. 1) При значении аргумента, равном х, имеем y= x 2 . При значении аргумента, равном х+ x , имеем

у+ y = (х+ x ) 2 .Найдем приращение функции

y = (х+ x ) 2 х 2 = 2х x + ( x ) 2 . Составляем отношение

2) При х=3 получим y x 3 2 3 6.

3.3. Дифференцируемость функций

Если функция y=f(x) имеет производную в точке x0, т.е.

дифференцируема в точке x0. Если функция дифференцируема в каждой точке отрезка [a ,b], то она дифференцируема на от-

резке [a, b].

Теорема. Если функция f(x) дифференцируема в некоторой точке x0, то она непрерывна в этой точке.

Обратное заключение неверно. Из того, что функция непрерывна в точке, не следует, что она дифференцируема, т.е. непрерывная функция может не иметь производной.

Пример 3.2. Функция f(x) определена на отрезке [0, 2] следующим образом (рис.14):

36

Таким образом, рассматриваемый предел зависит от того, каков знак х, а это значит, что в точке х=1 функция не имеет производной. По определению производной требуется, чтобы

отношение y при х 0 стремилось к одному и тому же пре-

x

делу независимо от того, каким образом стремится к нулю х. Геометрически это означает, что в точке х=1 данная «кривая» не имеет касательной.

37

Пример 3.3. Функция y 3 x (рис. 15) определена и непрерывна для любого x. Найдем производную в точке x=0.

В данной точке тангенс угла наклона касательной не определен и касательная образует с осью Ох угол 2 .

3.4. Правила дифференцирования Теорема 1. Производная постоянной равна 0, т.е. если

y c , где с =const , то

Теорема 3. Производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций, т.е. если y u(x) v(x) , то

Теорема 4. Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение производной второй функции на первую, т.е. если y u v, то

Теорема 5. Производная частного двух дифференцируемых функций равна дроби, у которой знаменатель равен квадрату знаменателя, а числитель есть разность произведений производной числителя на знаменатель и производной знаме-