
- •1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1.1.1. Понятие функции
- •1.1.2. Способы задания функций
- •1.1.4. Классификация функций
- •2.1. Предел функции
- •2.2. Бесконечно большая и ограниченная функции
- •2.3. Бесконечно малые и их основные свойства
- •Вопросы для самопроверки
- •3.6. Производные элементарных функций
- •Правила дифференцирования
- •Уравнения (3.9) называются параметрическими уравнениями кривой, а t – параметром.
- •Вопросы для самопроверки
- •Замечание 2. Если производная существует не во всех точках внутри [a,b], то утверждение может оказаться неверным, т.е. на отрезке может не оказаться точки в которой производная обращается в нуль. Например:
- •4.2. Теорема Лагранжа
- •Приведем теорему о конечных приращениях.
- •Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •6.1. Предельные показатели в микроэкономике
- •6.2. Максимизация прибыли
- •8.4. Интегрирование с помощью замены переменной
- •Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
- •11.12.5. Оптимизация спроса
- •12.1. Основные понятия и определения
- •Теорема. Если в уравнении
- •Определение. Общим решением дифференциального уравнения первого порядка называется функция
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •11.12.5. Оптимизация спроса…………………………174
- •12.1. Основные понятия и определения…………………177
- •12.11.4. Неоклассическая модель роста……………..214

Замечание 3. Обратное утверждение неверно. Неограниченная функция может не быть бесконечно большой. Например, y x sin x при x неограниченна, так как для любого
М > 0 можно указать такие значения x, что x sin x M . Но функция y x sin x не является бесконечно большой, так как обращается в нуль при x k .
2.3. Бесконечно малые и их основные свойства
Определение 1. Функция (x) называется бесконечно
малой при x a |
или при |
|
x , |
если lim (x) 0 , или |
||||||
|
|
|
|
|
|
|
|
|
|
x a |
lim (x) 0 . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
Пример 2.4. |
Функция |
|
|
1 |
|
будет бесконечно малой |
||||
|
x |
|||||||||
|
|
|
|
|
|
|
|
|||
при x , так как lim |
1 |
|
0 . Действительно, из определе- |
|||||||
|
||||||||||
|
|
x x |
|
|
|
|
|
|
||
ния предела следует, что для любого наперед заданного произвольно малого положительного найдется такое число N, что для всех значений х, удовлетворяющих неравенству |x| > N,
1 |
0 |
. Имеем |
1 |
, |
| x | |
1 |
, тогда |
N |
1 |
, |
|
x |
x |
|
|
||||||||
|
|
|
|
|
|
|
| x | N 1 .
Пример 2.5. Функция (2 x)3 при x 2 является
бесконечно малой, так как lim (2 x)3 0. x 2
Теорема 1. Если функция y f (x) представлена в виде суммы постоянного числа b и бесконечно малой α: у = b + α, то lim y b (при x a , x ).
Обратно, если lim y b , то у = b + α.
16

Пример 2.6. Пусть дана |
функция y 1 |
1 |
. Тогда |
|
x |
||||
|
|
|
||
lim y 1. И наоборот, так как |
lim y 1, то переменную у |
|||
x |
x |
|
|
|
можно представить в виде суммы предела 1 и бесконечно малой , равной в данном случае равна 1/x, т.е. у =1+ .
Теорема 2. Если (x) 0 при x a ( x ) и не
обращается в 0, то y 1 стремится к бесконечности.
Теорема 3. Алгебраическая сумма конечного числа бесконечно малых есть функция бесконечно малая.
Теорема 4. Произведение бесконечно малой функции(x) на ограниченную z z(x) при x a ( x ), есть бесконечно малая функция.
Cледствие 1. Если lim 0 , lim 0 , то lim 0 . Следствие 2. Если lim 0 , c const , то lim c 0 .
Теорема 5. Частное ( x) от деления бесконечно малой z( x)
величины (x) на функцию, предел которой отличен от 0, есть величина бесконечно малая.
2.4. Основные теоремы о пределах
Будем рассматривать совокупность функций, которые зависят от одного и того же аргумента х, при этом x a или x . Поэтому не будем писать ни x a , ни x , подразумевая то или другое.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных:
lim u1 u2 ... uk lim u1 lim u2 ... lim uk
17

Пример 2.7.
lim 5x 2 6x x x 2
|
|
lim 5 |
|
x |
|
6 |
lim |
5 lim |
6 |
5 . |
|
|
|
|
|||
|
|
||||
x |
x |
x x |
|
||
Теорема 2. Предел произведения двух, трех и вообще определенного числа переменных равен произведению пределов этих переменных.
lim u1 u2 ... |
uk lim u1 lim u2 ... |
lim uk |
Следствие. Постоянный множитель можно выносить за знак предела:
lim u1 a1, |
lim cu1 lim c lim u1 c lim u1. |
||
Пример 2.8. |
lim 5x 2 |
5 lim x 2 |
5 4 20 . |
|
x 2 |
x 2 |
|
Теорема 3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя
отличен от 0: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
u |
|
lim u |
|
при lim v 0 . |
|
|||||
|
|
v |
lim v |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
Пример 2.9. |
|
|
|
|
|
|
|
|
|||||
|
2x 1 |
|
lim (2x 2) |
|
2 lim x 2 |
|
4 |
|
|||||
lim |
|
x 1 |
|
x 1 |
|
1. |
|||||||
4x 8 |
lim (4x 8) |
4 lim x 8 |
4 |
||||||||||
x 1 |
|
|
|
|
|||||||||
|
|
|
x 1 |
|
x 1 |
|
|
|
|||||
Теорема 4. Если между соответствующими значениями трех функций u u(x); z z(x); v v(x) выполняются неравен-
ства u z v , при этом u и v при x a или x стремятся к одному и тому же пределу b, то z=z(x) при x a (или при x ) стремится к тому же пределу.
18

Теорема 5. Если при x a (или при x ) функция y принимает неотрицательные значения y 0 и при этом y b ,
то b есть неотрицательное число b 0 .
Теорема 6. Если между соответствующими значениями двух функций u u(x) и v=v(x), стремящихся к пределам при
x a (или при x ) выполняется неравенство u(x) v(x) , то имеет место lim u(x) lim v(x) .
Теорема 7. Если переменная величина v возрастающая, т.е. всякое ее последующее значение больше предыдущего, и, если она ограничена, т.е. v < M, то эта переменная величина имеет предел lim v a , где а < M.
Примеры. 2.10. Вычислить пределы
1)
|
5x2 3x 1 |
|
|
lim (5x2 3x 1) |
|
5 lim x2 3 lim x 1 |
|
7 |
|
||
lim |
|
|
x 1 |
|
x 1 |
x 1 |
|
|
. |
||
|
|
|
|
|
|||||||
x 1 x2 3x 4 |
|
lim (x2 3x 4) |
|
lim x2 3 lim x 4 |
|
2 |
|
||||
|
|
|
|
x 1 |
|
x 1 |
x 1 |
|
|
|
|
2
2) lim . Здесь предел знаменателя равен 0. Восполь- x 1 x 1
зуемся теоремой о том, что величина, обратная бесконечно малой, будет бесконечно большой величиной. Таким образом,
lim |
2 |
|
|
2 |
. |
|
|
|
|||
x 1 x 1 |
|
0 |
|
||
Здесь и в дальнейшем будем обозначать бесконечно малую величину -0, а бесконечно большую величину - .
Выражения вида 0 , , 0 , , 1 называют-
0
ся неопределенностями.
19

|
|
|
|
|
|
2.5. Предел функции |
|
sin x |
при x 0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
(первый замечательный предел) |
|
|||||||||||||||
Функция |
|
sin x |
|
не определена при x 0 , так как числи- |
||||||||||||||||||||
|
|
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тель |
и |
знаменатель дроби обра- |
|||||||
|
|
|
|
|
|
|
М |
|
|
|
|
С |
||||||||||||
|
|
|
|
|
|
|
|
|
|
щаются |
|
в нуль. Найдем |
предел |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
этой |
|
функции |
при |
x 0 . Рас- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
смотрим окружность радиуса 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
(рис. 6). Обозначим центральный |
|||||||||
О |
|
|
|
|
|
|
|
|
|
|
|
|
А |
угол |
|
|
через |
х. |
При |
этом |
||||
|
|
|
|
|
В |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
0 x 2 . Из |
рис. |
6 |
следует, |
|||||||||||||
|
|
Рис. 6 |
|
|
||||||||||||||||||||
|
|
|
|
что площадь МОА площади |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сектора МОА площади СОА. |
|||||||||
Площадь MOA 1 |
2 |
OA MB 1 |
2 |
1 sin x 1 |
2 |
sin x . Площадь |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сектора МОА = 12 OA AM 12 1 x x 2 . Площадь
СОА = 12 OA CA 12 1 tgx . После сокращения на ½ полу-
чим sin x x tgx .
Разделим все члены на sin x |
|
|
|
||||||
1 |
x |
|
1 |
|
или |
1 |
sin x |
cos x . |
|
sin x |
cos x |
|
|||||||
|
|
|
|
|
|
x |
|||
Мы вывели это неравенство в предположении, что х 0. |
|||||||||
Но оно верно и для х 0. Но |
lim cos x 1, lim 1 1. |
||||||||
|
|
|
|
x 0 |
|
x 0 |
|||
Переменная величина |
|
sin x |
|
заключена между двумя ве- |
|||||
|
x |
||||||||
|
|
|
|
|
|
|
|
||
личинами, имеющими предел равный 1. Следовательно, на основании теоремы 4 предыдущего параграфа
lim sin x 1 . x 0 x
20
Примеры 2.11.
1) |
lim |
tg3x |
lim |
|
3sin 3x |
3 lim |
sin 3x |
3. |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
x 0 |
x |
x 0 3x cos 3x |
x 0 |
3x |
||||||||||||
Здесь было использовано, что lim cos 3x 1. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|||
2) |
lim |
sin 3x |
lim |
sin 3x 3 5x |
|
3 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
x 0 sin 5x |
x 0 |
3x |
|
|
sin 5x |
5 |
|
|
||||||||
|
2.6. Число e. Второй замечательный предел |
||||||||||||||||
|
|
|
|
|
|
|
1 x |
|
|
|
|
|
|||||
Теорема. Функция 1 |
|
|
|
|
при х, |
стремящемся к беско- |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||
нечности, стремится к пределу е:
|
|
|
1 x |
|
||
lim |
1 |
|
|
=е. |
(2.2) |
|
|
||||||
x |
|
|
x |
|
|
|
Если в равенстве (2.2) положить 1/x =, то при |
|
x |
||||||||||||||||||||||||||||||||
имеем 0 и получаем |
lim |
1 1/ =е. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Число е иррациональное число. Его значение с десятью |
||||||||||||||||||||||||||||||||||
верными знаками после запятой: е =2, 7182818284... |
|
|
|
|||||||||||||||||||||||||||||||
Примеры 2.12: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 x 6 |
|
|
|
|
|
|
|
1 x |
|
|
1 |
6 |
|
|
|
|
||||||||||||||
1. lim |
1 |
|
|
|
|
|
|
= lim |
|
1 |
|
|
|
|
|
1 |
|
|
|
= |
|
|
|
|||||||||||
x |
|
|
|
x |
|
x |
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
||||||||||||||
|
|
|
1 x |
|
|
|
|
1 6 |
= е 1=е. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= lim |
1 |
|
|
|
|
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
|
|
x |
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 3x |
|
|
|
|
|
|
|
1 x |
|
|
|
1 x |
|
|
1 x |
||||||||||||||
2. lim |
1 |
|
|
|
|
|
|
|
|
= lim |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
|
|
|
|
x |
|
x |
|
|
|
|
x |
|
|
|
x |
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
1 |
x |
|
|
|
|||||
= lim |
1 |
|
|
|
|
|
|
|
lim |
1 |
|
|
|
|
lim |
1 |
|
|
= |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
x |
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= е е е = e3.
|
lim 1 |
2 |
|
|
x |
|
|
|
|
|
|
1 |
|
2 y |
e2 |
|
|
|
|
|
|
|||||||||
3. |
|
|
|
|
lim |
1 |
|
|
|
|
. 1. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x 3 |
|
x 3 |
|
x 1 4 x 3 |
|
|
|
|
|||||||||||||||||||||
4. |
lim |
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x x 1 |
|
|
|
|
x |
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
x 3 |
|
|
|
|
|
|
|
|
|
|
4 x 1 4 |
|
|
|
|||
|
= lim |
1 |
|
|
|
|
|
|
|
= |
lim |
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
|
|
|
|
x |
1 |
|
x |
|
|
|
|
x |
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
4 |
y 4 |
|
|
|
|
|
|
4 |
y |
|
|
|
4 |
|
4 |
|||||||
|
= lim |
1 |
|
|
|
|
|
|
= lim |
|
1 |
|
|
lim 1 |
|
|
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
y |
|
|
|
y |
|
|
y |
|
|
|
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||||||
=e4 1 e4 .
2.7.Раскрытие некоторых неопределенностей
Рассмотрим предел функции lim |
f ( x) |
( или при x ), |
|
g( x) |
|||
x a |
|
который при непосредственной подстановке х = а приходит к одному из случаев неопределенности. Укажем приемы для решения таких примеров, приемы «раскрытия неопределенности».
1. В числителе и знаменателе многочлены. Получается
неопределенность . Для ее раскрытия необходимо разде-
лить числитель и знаменатель на x в старшей степени.
Пример 2.13.
lim |
x |
2 x 1 |
lim |
|
x 2 / x 2 x / x 2 1/ x 2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||
x 2x 2 x |
x |
|
|
|
2x 2 / x 2 |
x / x 2 |
|
|||||
lim |
1 1/ x 1/ x 2 |
|
1 |
. |
|
|
||||||
|
2 1/ x |
|
2 |
|
|
|||||||
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
22 |
|
|

Здесь было использовано, что при x величины 1/x и 1/ x 2 стремятся к нулю.
2. В числителе и знаменателе многочлены. Получается
неопределенность вида |
0 |
|
. Для решения надо разложить |
|
|
|
|
||
|
||||
|
0 |
|
|
|
числитель и знаменатель на множители и сократить.
Пример 2.14.
lim |
4x 3 2x 2 x |
lim |
x(4x 2 2x 1) |
|
1 |
. |
|
3x 2 2x |
x(3x 2) |
2 |
|||||
x 0 |
x 0 |
|
|
3. Дробь не является рациональной т.е. в числителе или знаменателе есть корни. Получается неопределенность вида
0 . Необходимо числитель и знаменатель умножить и разде-
0
лить на сопряженное и сократить.
Пример 2.15.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
(3 |
|
1)(3 x 2 |
3 |
|
|
1) |
|
|||||
|
x 1 |
lim |
x |
x |
|
|||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(x 1)(3 x 2 |
|
|
|
|
|
||||||||||||
x 1 |
x 1 |
3 |
|
1) |
|
|||||||||||||
x |
|
|||||||||||||||||
lim |
|
|
|
|
|
(x 1) |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 1 |
|
|
|
|
|
3 |
|
|
2 |
|
3 |
|
|
|
|
|
|
x 1 |
|
3 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
3 |
|||||||
(x |
1)( |
x |
|
x 1) |
( |
|
x |
|
x 1) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 2.16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
x 2 |
1 1 |
lim |
|
|
( x 2 1 1)( |
|
|
|
x 2 1 1) |
|
|
|
||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x 0 |
|
|
|
|
|
|
x 0 |
|
|
|
x( x 2 1 1) |
|
|
|
|
|
|
|
||||||||||||||||||||||
lim |
|
(x 2 1) 1 |
|
|
lim |
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
0. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x 0 x( x 2 1 1) |
|
x 0 x( x 2 1 1) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. При непосредственном вычислении получается неопределенности вида . В выражении есть корни. Необходимо умножить и разделить на сопряженное.
Пример 2.17.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
2 |
1 |
|
|
|
x |
2 |
|
|
|
x |
2 |
1 |
|
x |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 1 x 2 1 |
|
|
|
|
||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
x 2 |
1 |
x 2 |
1 |
|
2 |
0 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
x |
x |
2 |
1 |
|
x |
2 |
1 |
|
|
||||
|
|
|
|
|
|
|
|||||||
5.Неопределенность вида . Необходимо привести
кобщему знаменателю. В результате получим один из уже рассмотренных случаев.
Пример 2.18. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
3 |
|
|
|
1 x x 2 |
3 |
0 |
|
|
||||
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|||
|
x |
|
x3 |
1 x3 |
|
|
|
||||||||||
x 1 |
1 |
1 |
|
|
x 1 |
|
|
0 |
|
|
|||||||
lim |
|
|
|
(x 1)(x 2) |
|
1. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 |
x)(1 x x |
2 ) |
|
|
|
|
|
|
|||||||||
x 1 |
|
|
|
|
|
|
|
|
|||||||||
6. Пример содержит тригонометрические функции. По-
0
лучается неопределенность вида . Для решения необхо-
0
димо воспользоваться первым замечательным пределом.
24

2.8. Непрерывность функции
Пусть функция у = f(x) определена при некотором значении х0 и в некоторой окрестности с центром в х0. Пусть
у0 = f(x0). Если х получит некоторое положительное или отрицательное приращение и примет значение х=х0 + х, то и функция у получит некоторое приращение у. Новое, значение функции будет (рис. 7) у0 + у = f(x0 + х). Приращение функции у выразится формулой у = f(x0+ х) f(x0).
y |
|
|
|
|
|
|
|
|
|
М |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
М0 |
|
|
|
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
у0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
х |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
х0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||
|
|
|
|
|
|
|
х0+ х |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.7
Определение 1. Функция у = f(x) называется непрерыв-
ной при значении х=х0 (или в точке х0), если она определена в некоторой окрестности точки х0 и если
или, что то же самое,
lim [ fx 0
Условие непрерывности
limx 0
lim y 0 |
(2.3) |
x 0 |
|
(x0 x) f (x0 )] 0 . |
(2.4) |
(2.4) можно записать так |
|
f (x0 x) f (x0 ) . |
(2.5) |
Следствие. Для того, чтобы найти предел непрерывной функции при х х0, достаточно в выражение функции подставить вместо аргумента х его значение х0.
25
Пример 2.19. Доказать, что функция y x 2 непрерывна в произвольной точке х0. Действительно,
y0 x02 ; y0 y (x0 x)2 ,
y (x0 x)2 x02 2x0 x x2 .
lim y = lim (2x0 x x 2 )x 0 x 0
=2x0 lim x + lim x lim x =0x 0 x 0 x 0
при любом стремлении x к нулю к нулю.
Теорема 1. а) Если функции f1(x) и f 2(x) непрерывны в точке х0, то сумма (х ) = f1(x) + f 2(x) также есть непрерывная функция в точке х0.
б) Произведение двух непрерывных функций есть функция непрерывная.
в) Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.
г) Если u = (х) непрерывна при х=х0 и f(u) непрерывна в точке u0= (х0), то сложная функция f( (х)) непрерывна в
точке х0.
Теорема 2. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Пример 2.20. Функция |
y x 2 непрерывна в произволь- |
||
ной точке х0 и поэтому |
|
|
|
lim x 2 x 2 |
, |
lim |
x 2 32 9. |
0 |
|
|
|
x x0 |
|
x 3 |
|
Определение 2. Если функция у = f (х) непрерывна в каждой точке некоторого интервала (а,b), где а b, то гово-
рят, что функция непрерывна на этом интервале.
Если функция определена при х = а и при этом
26

lim f (x) f (a) , то говорят, что f (х) в точке х=а непрерыв- x a 0
на справа.
Если функция определена при х = с и при этом
lim f (x) f (c) , то говорят, что f (х) в точке х= с непрерыв- x c 0
на слева.
Если функция у = f (х) непрерывна в каждой точке некоторого интервала (а,b) и непрерывна на концах интервала соответственно справа и слева, то говорят, что функция непре-
рывна на замкнутом интервале или отрезке [a,b].
Определение непрерывной функции (2.5) можно записать иначе.
Определение 3. Функция у = f (х) непрерывна в точке х0
если:
1) |
функция определена в точке х0, |
|
|||
2) |
существуют lim |
f (x) , и lim |
f (x) , |
||
|
|
x x0 0 |
x x0 |
0 |
|
3) |
выполняется равенство |
|
|
||
|
lim |
f (x) = |
lim |
f (x) = f (х0). |
|
|
x x0 |
0 |
x x0 |
0 |
|
Если хотя бы одно из требований непрерывности не выполнено, то в точке х0 функция у = f (х) разрывна. Точка х=х0 в этом случае называется точкой разрыва.
Пример 2.21. Функция у=1/x разрывна при х=0. Действительно, при х=0 функция не определена:
lim 1/ x , и x 0
lim 1/ x . x 0
Во всех других точках функция непрерывна.
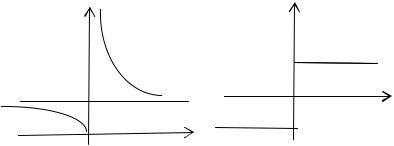
Пример 2.22. Функция |
y 21/ x разрывна. Действитель- |
но, при х=0 функция не определена (рис. 8) и |
|
lim 21/ x , и |
lim 21/ x 0. |
x 0 |
x 0 |
|
27 |
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
у= x / |
|
|
|
||||
|
у= 21/ x |
|
|
|
|
|
|
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
0 |
-1 |
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
|
|
|
|
|
|
|
Рис. 9 |
|
||||||||
Пример 2.23. Рассмотрим функцию у=х/ x . В точке х=0 |
|||||||||||||||||||||
функция не определена. При х 0 будет |
х/ x |
= 1; при х 0 |
|||||||||||||||||||
будет х/ x =1. Следовательно, |
lim |
f (x) |
lim |
x / |
|
x |
|
1, |
|
||||||||||||
|
|
|
|||||||||||||||||||
lim f (x) lim |
x / |
|
x |
|
1. |
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x 0 |
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В точке х=0 функция разрывна (рис. 9). |
|
|
|
|
|
|
|
|
|||||||||||||
Определение 4. Если функция у = f (х) такова, что суще- |
|||||||||||||||||||||
ствуют |
конечные |
пределы |
lim |
|
f (x) f (x0 0) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
x x0 |
0 |
|
|
|
|
|
|
|
|
|||
и lim |
f (x) f (x0 0) , но |
или |
lim |
|
|
f (x) lim |
f (x) , |
||||||||||||||
x x0 0 |
|
|
|
|
|
|
|
|
x x0 |
0 |
|
x x0 0 |
|
||||||||
или значение функции не определено при х=х0 , то х=х0 |
назы- |
||||||||||||||||||||
вается точкой разрыва 1-го рода (рис. 9).
Если хотя бы один из пределов справа и слева не является конечным, то имеем разрыв второго рода (рис. 8).
28
2.9. Некоторые свойства непрерывных функций
Рассмотрим некоторые свойства функций непрерывных на отрезке.
Теорема 1. Если функция у = f (х) непрерывна на некотором отрезке [a,b], то на отрезке [a,b] найдется по крайней мере одна точка х=х1 такая, что значение функции в этой точке будет удовлетворять соотношению f ( х1) f (х), где х – любая другая точка отрезка, и найдется по крайней мере одна точка х=х2 такая, что значение функции в этой точке будет удовлетворять соотношению f (х2) f (х).
Значение функции f (х1) будем называть наибольшим значением функции у = f (х) на отрезке [a,b], а значение функции
f (х2) будем называть наименьшим значением функции у = f (х)
на отрезке [a,b].
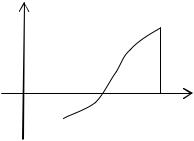
Теорема 2. Пусть функция у = f (х) непрерывна на некотором отрезке [a,b], и на концах этого отрезка принимает значения разных знаков, тогда между точками a и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль.
Эта теорема имеет простой геометрический смысл. График функции у = f (х) непрерывной на отрезке [a,b], которая на концах отрезка принимает значения разных знаков, пересекает ось Ох по крайней мере в одной точке (рис. 10).
y |
М2(b,f(b)) |
,f(b)
|
|
а |
с |
b |
||
|
|
|
|
|
|
|
0 |
|
|
|
|
x |
|
|
,f(a) |
|
|
|||
|
||||||
|
|
|
|
|
|
|
М1(а,f(a))
Рис. 10
29
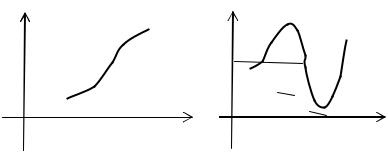
Теорема 3. Пусть функция у = f (х) определена и непрерывна на отрезке [a,b]. Если на концах этого отрезка функция принимает неравные значения f (а)= А, f (b) =B, то каково бы ни было число , заключенное между А и В, найдется такая точка х=с, заключенная между а и b , что f (с)= .
Смысл данной теоремы иллюстрируется на рис. 11. В данном случае всякая прямая у = пересекает график функции у = f (х).
Следствие. Если функция у = f (х) непрерывна на некотором интервале и принимает наибольшее и наименьшее зна-
чения |
, |
то на этом интервале она принимает по крайней мере |
||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=f(c) |
|
|
|
М |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
а |
|
|
|
b x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
b |
|
||||||
|
|
|
|
|
|
|
с |
|
|
а |
|
x1 |
|
|
|
x2 |
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|
|
Рис. 12 |
||||||||||||
один раз любое значение, заключенное между ее наибольшим и наименьшим значениями (рис.12).
2.10. Сравнение бесконечно малых
Пусть одновременно несколько бесконечно малых величин , , , являются функциями одного и того же аргумента х, стремятся к нулю при стремлении х к некоторому пределу а или к бесконечности.
Определение 1. Если отношение / имеет конечный и отличный от нуля предел, т.е. lim / A 0 , а следователь-
но, lim / 1/ A 0 , то бесконечно малые и называются
бесконечно малыми одного порядка.
30
Пример 2.24. Пусть =х, =sin 2x, где х 0. Бесконечно малые и одного порядка, так как
lim |
|
lim |
sin 2x |
2 lim |
sin 2x |
2. |
|
|
|
|
|
||||
x 0 |
x 0 |
x |
x 0 |
2x |
|
||
|
Определение 2. Если отношение двух бесконечно малых |
||||||
/ стремится к нулю, т.е. lim / 0 |
(а lim / ), то |
||||||
бесконечно малая называются бесконечно малой величиной высшего порядка, чем бесконечно малая , а бесконечно малаяназывается бесконечно малой низшего порядка, чем бесконечно малая .
Пример. 2.25. Пусть =х, = x n , n 1 х 0. Бесконечно малая есть бесконечно малая высшего порядка, чем беско-
нечно малая , так как lim |
|
lim |
x n |
lim x n 1 0. |
|
|
x |
||||
x 0 |
x 0 |
x 0 |
При этом бесконечно малая есть бесконечно малая низшего порядка, чем бесконечно малая .
Определение 3. Если отношение двух бесконечно малых/ стремится к единице, т.е. lim / 1, то бесконечно ма-
лые и называются эквивалентными бесконечно малыми и
пишут .
Пример 2.26. Пусть =х, =ln(1+ х), где х 0. Бесконечно малые и эквивалентны, так как
lim |
|
lim |
ln(1 x) |
lim |
1 |
ln(1 x) lim ln[(1 x)1/ x ]. |
|
|
|
||||
x 0 |
x 0 |
x |
x 0 x |
x 0 |
||
Так как lim (1 x)1/ x e и функция ln z непрерывна при z >0 а, x 0
следовательно, и при z = е, то
31
