
- •1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1.1.1. Понятие функции
- •1.1.2. Способы задания функций
- •1.1.4. Классификация функций
- •2.1. Предел функции
- •2.2. Бесконечно большая и ограниченная функции
- •2.3. Бесконечно малые и их основные свойства
- •Вопросы для самопроверки
- •3.6. Производные элементарных функций
- •Правила дифференцирования
- •Уравнения (3.9) называются параметрическими уравнениями кривой, а t – параметром.
- •Вопросы для самопроверки
- •Замечание 2. Если производная существует не во всех точках внутри [a,b], то утверждение может оказаться неверным, т.е. на отрезке может не оказаться точки в которой производная обращается в нуль. Например:
- •4.2. Теорема Лагранжа
- •Приведем теорему о конечных приращениях.
- •Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •6.1. Предельные показатели в микроэкономике
- •6.2. Максимизация прибыли
- •8.4. Интегрирование с помощью замены переменной
- •Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
- •11.12.5. Оптимизация спроса
- •12.1. Основные понятия и определения
- •Теорема. Если в уравнении
- •Определение. Общим решением дифференциального уравнения первого порядка называется функция
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •11.12.5. Оптимизация спроса…………………………174
- •12.1. Основные понятия и определения…………………177
- •12.11.4. Неоклассическая модель роста……………..214

Замечание 1. Равенство справедливо, если в условии
(4.5) А= .
Замечание 2. Теорема справедлива если x
|
f (x) |
|
|
|
|
|
|
|
|
|
f (x) |
|
|||
lim |
|
|
|
|
lim |
|
. |
|
|
||||||
x g(x) |
|
|
|
x g (x) |
|
||
Остальные случаи неопределенностей сводятся к рассмотренным.
Примеры 4.3.
Вычислить пределы, используя правило Лопиталя.
|
e x2 |
1 |
0 |
|
|
e x2 2x |
0 |
|
|
|||
1) lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 0 cos x1 |
|
0 |
|
x 0 |
sin x |
|
0 |
|
|
|||
|
lim |
e x2 |
2x2x e x2 2 |
|
2 |
|
2. |
|
cos x |
1 |
|||||
|
x 0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
ln sin(2x) |
|
|
|
|
||
2) lim |
|
|
|
|
|
||
|
|
||||||
x 0 |
|
ln sin x |
|
|
|
|
|
lim |
sin xcos(2x)2 |
|
|
||||
2sin xcos xcos x |
|||||||
x 0 |
|
||||||
|
|
1 |
cos(2x)2 |
|
|
|
|
|
|
lim |
|
sin(2x) |
|
|
|
1 |
|
x 0 |
cos x |
|
|
sin x |
|
1. |
|
|
Вопросы для самопроверки
1. Приведите правило Лопиталя для раскрытия неопреде-
0
ленности вида , .0
56
Задачи для самостоятельного решения
|
|
|
e x e x |
|
|
||
1. |
lim |
|
|
. |
Ответ. |
2. |
|
|
|
||||||
|
x 0 |
sin x |
|
|
|||
2. |
lim |
|
tgx x |
. |
Ответ. |
2. |
|
|
|
||||||
|
x 0 x sin x |
|
|
||||
3. lim |
ln tg7x |
. |
Ответ. 1. |
|
|||
x 0 ln tg 2x1 |
|
||
4. lim |
ln x |
, (n 0). |
Ответ. 0. |
|
|||
x x n |
|
|
|
5. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
5.1. Возрастание и убывание функции
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции.
Применим понятие производной для исследования возрастания функции.
Теорема 1. 1) Если функция f(x), имеющая производную на отрезке [a,b], возрастает на этом отрезке, то ее производная на отрезке [a,b] не отрицательна, т.е. f (x) 0 .
2) Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема в промежутке (a,b), причем f (x) 0 для
x (a,b), то функция возрастает на отрезке [a,b].
Аналогичная теорема имеет место и для убывающих (дифференцируемых) функций, а именно:
Теорема 2. 1) Если функция f(x), имеющая производную на отрезке [a,b], убывает на этом отрезке, то ее производная на отрезке [a,b] f (x) 0 .
57
2) Если функция f(x) непрерывна на отрезке [a,b] и дифференцируема в промежутке (a,b), причем f (x) 0 для
x (a,b), то функция убывает на отрезке [a,b].
Замечание. Если на отрезке [a,b] функция возрастает, то касательная к кривой у=f(x) в каждой точке образует c осью Ох или острый угол или - в отдельных точках –горизонтальна . Тангенс этого угла не отрицателен.
Если на отрезке [a,b] функция убывает, то касательная к кривой у=f(x) в каждой точке образует c осью Ох или тупой уголили - в отдельных точках –горизонтальна . Тангенс этого угла не положителен.
Примеры 5.1. Найти интервалы возрастания и убывания
функции: |
|
|
1) y= x 2 . Производная равна y 2x . При x>0 |
y 0 – |
|
функция возрастает. При x<0 y 0 – функция убывает. |
||
2) y= x 3 . Производная равна y 3x 2 . |
Производная |
|
y 0 для любого х – функция всюду возрастает. |
|
|
5.2. Максимум и минимум функции |
|
|
Определение 1. Функция f(x) в точке x=a имеет макси- |
||
мум, если f(a+Δx)<f(a) при любых достаточно малых |
x. |
|
Определение 2. Функция f(x) точке x=a имеет минимум, |
||
если f(a+Δx)>f(a) при любых достаточно малых |
x. |
|
В связи с определением максимума и минимума следует обратить внимание на следующие обстоятельства.
58

y
|
b |
х |
||
0 |
a х1 х2 х3 х4 |
|||
|
|
|||
Рис. 21
1)Функция, определенная на отрезке, достигает максимума и минимума только внутри отрезка.
2)Максимум и минимум не являются соответственно наибольшим и наименьшим значением функции на рассматриваемом отрезке, в точке максимума функция имеет наибольшее значение только по сравнению с достаточно близкими значениями.
Так на рис. 21 изображена функция, определенная на отрезке [a,b], которая
при x x1 и x x3 имеет максимум, при x x2 и x x4 имеет минимум.
Но минимум функции при х=х4 больше максимума функции при х=х1. При х=b значения функции больше любого максимума.
Максимумы и минимумы функции называются экстре-
мумами.
5.3. Необходимое и достаточное условия существования экстремума
Теорема 1. (необходимое условие существования экс-
тремума). Если дифференцируемая функция f(x) имеет в точке x=x1 максимум или минимум, то ее производная обращается в нуль в этой точке, т.е. f (x1)=0.
59
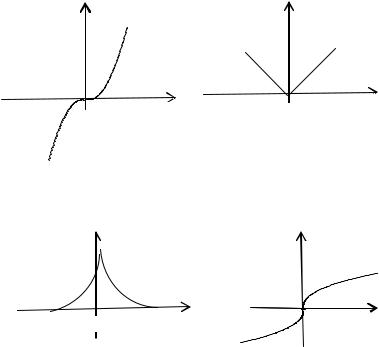
Геометрический смысл.
Если в точках максимума и минимума функция имеет производную, то касательная к графику в этих точках параллельна оси Оx.
Следствие. Если при всех рассматриваемых значениях аргумента функция имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль.
Обратное утверждение неверно. Если при некотором значении аргумента производная обращается в нуль, то функция не обязательно имеет экстремум.
Например, функция y x 3 имеет производную y 3x 2 , при x=0 производная равна нулю, но функция всюду
возрастает (рис. 22). |
|
|
|
y |
у=x 3 |
y |
у= х |
|
|
||
0 |
x |
0 |
x |
|
|||
Рис. 22 |
|
|
Рис. 23 |
Рассмотрим случай, |
когда в некоторых точках отрезка |
||
[a,b] производная не существует. Покажем на примерах, что в таких точках тоже может быть экстремум функции.
y |
|
|
y |
|
|
|
|
|
|
1 |
|
|
|
|
-1 0 |
1 |
x |
0 |
x |
|
||||
Рис. 24 |
|
|
Рис. 25 |
|
|
|
|
60 |
|
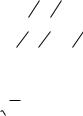
|
Примеры 5.2. Рассмотрим |
функции: 1) y=|x|, |
|
|
x, x 0 |
|
y не существует, но в |
y |
|
в точке x=0 производная |
|
x, x 0 |
|
|
|
этой точке функция имеет минимум, так как в любой отличной от нуля точке y>0 (рис. 23).
2) |
Функция y (1 x 2 3 ) 32 |
не |
имеет производной при |
||||||
х=0, так |
как |
y (1 x |
2 |
3 ) |
1 |
2 x |
1 |
3 |
обращается в бесконеч- |
|
|
|
|||||||
ность при х=0, но в этой точке функция имеет максимум
(рис. 24).
3) Функция y 3 x не имеет производной при х=0. В этой точке функция экстремума не имеет (рис. 25).
x не имеет производной при х=0. В этой точке функция экстремума не имеет (рис. 25).
Таким образом, если при некотором значении аргумента производная функции не существует, то экстремум в той точке может быть, а может и не быть. Отсутствие производной не является достаточным условием экстремума.
Функция может иметь экстремум, если производная f (х) =0 или f (х) не существует.
Значения аргумента при которых f (х) =0 или f (х) не
существует называются критическими точками первого рода.
Теорема 2. (достаточное условие экстремума). Пусть функция f(x) непрерывна в некотором интервале, содержащем критическую точку x1 и дифференцируема во всех точках этого интервала (за исключением, может быть x1). Если при переходе слева направо через эту точку производная меняет знак с «+» на « », то при x=x1 функция имеет максимум. Если при переходе слева направо через эту точку производная меняет знак с « » на «+», то при x=x1 функция имеет минимум.
Проиллюстрируем смысл теоремы на рисунке рис.33.
1) В точке x= x1 имеем f (х1) =0 и для всех х, достаточно близких к точке x1, выполняются неравенства f (х)>0 при
61
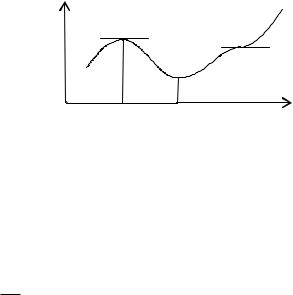
х <х1, функция возрастает; f (х)<0 при х >х1, функция убыва-
ет. Функция переходит от возрастания к убыванию, т.е. имеет максимум.
y
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 |
|
х2 |
|
|
|
х3 |
|
x |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 26
2)В точке x2 функция переходит от убывания к возрастанию, т.е. имеет минимум.
3)В точке x=x3 f (х)>0 при х <х3 и f (х)>0 при х>х3 , т.е. производная не меняет знак. Функция не имеет экстремума.
Пример 5.3. Найти экстремумы функции
y x 3 2x 2 3x 1. 3
Решение. Находим производную y x 2 4x 3. Приравняем производную нулю и найдем корни уравне-
ния x 2 4x 3 0.
Получим критические точки первого рода х1=1; х2=3. Критические точки разбивают числовую ось на интервалы. Найдем знак производной на каждом интервале. Результаты оформим в виде таблицы
|
|
|
|
|
Таблица 1 |
x |
- ,1 |
1 |
1 , 3 |
3 |
3 , |
y |
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
y |
↑ |
Max |
|
Min |
↑ |
|
возрастает |
y=7/3 |
убывает |
y=1 |
возрастает |
|
|
|
|
|
|
|
|
|
62 |
|
|
Функция имеет максимум уmax=7/3 при х=1 и минимум
уmin= 1 при х=3.
5.4. Наибольшее и наименьшее значение функции на отрезке
Пусть функция у=f(x) непрерывна на отрезке [a,b]. Тогда на этом отрезке функция достигает своего наибольшего значения. Если наибольшее значение достигается внутри отрезка , то это будет один из максимумов функции, а именно, наибольший максимум. Но наибольшее значение может достигаться и на концах отрезка. То же самое можно сказать и о наименьшем значении.
Можно сформулировать следующее правило: если тре-
буется найти наибольшее значение непрерывной функции на отрезке, то надо:
1)найти все критические точки и вычислить значения функции в критических точках;
2)найти значения функции на концах отрезка т.е. f(a) и
f(b).
3)из всех полученных значений выбрать наибольшее. Аналогичным образом следует поступать и при опреде-
лении наименьшего значения функции на отрезке.
Пример 5.4. Определить на отрезке [-3,3/2] наибольшее и наименьшее значение функции y=x³ -3x+3.
Решение. Из условия y 0 находим критические точки на отрезке [-3,3/2]: y 3x2 3 0; критические точки x1=1, x2=
-1. Значения функции в критических точках у(1)= 1, у(-1)= 5. Определим значения функции на концах отрезка
y(-3)= -15; y(3/2)=15/8.
Следовательно, наименьшее значение y(3)=-15 , наибольшее значение y(-1)=5.
63
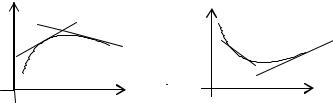
5.5. Выпуклость, вогнутость кривой. Точки перегиба
Определение 1. Кривая называется выпуклой на интер-
вале (a,b), если все ее точки расположены ниже любой ее касательной на этом интервале ( рис. 27).
Определение 2. Кривая называется вогнутой на интер-
вале (a,b), если все ее точки расположены выше любой ее касательной на этом интервале (рис. 28).
y |
y |
0 |
x |
0 |
|
x |
Рис. 27 |
|
|
Рис. 28 |
|
|
|
|||
Теорема 1. Если во всех точках интервала (a,b) вторая производная функции f`(x) отрицательна, т.е. f (x) <0, то кри-
вая выпукла на этом интервале.
Теорема 2. Если во всех точках интервала (a,b) вторая производная f (x) >0, то кривая вогнута на этом интервале.
Примеры 5.5. Установить интервалы выпуклости и вогнутости кривой.
1)y=x²; y 2x, y 2 > 0 для всех х. Кривая всюду во-
гнута.
2)y x 3 , y 3x 2 , y 6x . Следовательно, кривая выпукла при x<0 и вогнута при x>0.
Определение. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой называется точкой перегиба.
Установим достаточное условие того, что данная точка кривой является точкой перегиба.
64

Теорема 3. Пусть кривая определяется уравнением y=f(x). Если f (a)=0 или f (a) не существует и при переходе
через x=a вторая производная меняет знак, то точка кривой с абсциссой x=a есть точка перегиба.
Пример 5.6. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривой y x3 5x 2 3x 5.
Решение. Найдем первую и вторую производные y 3x 2 10x 3, y 6x 10 .
Первая и вторая производные существуют всюду. Находим значения х, при которых y 0 : x=5/3. Исследуем полученное значение.
При x<5/3, y <0. Кривая выпукла. При x>5/3, y >0. Кривая вогнута.
Точка (5/3,-250/27) является точкой перегиба.
5.6. Асимптоты
Определение. Прямая L называется асимптотной кривой, если при удалении точки M по кривой в бесконечность, расстояние от точки M до L 0 (рис. 29).
y |
|
y |
|
y |
|
|
|
|
|
|
|
0 |
x |
0 |
x |
0 |
|
|
x |
||||
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис. 29 |
|
|
Различают асимптоты наклонные и вертикальные. |
|||||
1.Вертикальные асимптоты. |
|
|
|||
Из |
определения |
асимптоты |
|
следует, что если |
|
lim f (x) или lim |
f (x) , |
то прямая x=a является |
|||
x a 0 |
|
x a 0 |
|
|
|
асимптотой.
65

Следовательно, вертикальные асимптоты могут быть в точках, где функция не определена.
Пусть при x=a функция не определена, если при x a f(x) , прямая x=a будет вертикальной асимптотой.
Примеры 5.7.
1) Кривая y 1x имеет вертикальную асимптоту х=0, так как у при х 0 (рис. 30).
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
у= e1/ x |
|
|||
|
|
у=1/ x |
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 30 |
|
Рис. 31 |
|||||
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
2) |
Кривая |
y e x имеет вертикальную асимптоту х=0, |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 31). |
|
|
|
|
||||
так как |
lim e x |
|
|
|
|
||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
2.Наклонные асимптоты. Пусть кривая y=f(x) имеет
нение которой: у=kx+b. Определим числа k и b:
k lim f ( x) x x
Зная k, определим b:
b lim [ f (x) x
наклонную асимптоту, урав-
. |
(5.1) |
kx]. |
(5.2) |
66 |
|

Итак, если прямая y=kx+b есть асимптота, то k и b находятся по формулам (5.1),(5.2). Обратно, есль существуют пределы (5.1), (5.2), то прямая y=kx+b есть асимптота. Если хотя бы один предел не существует, то асимптоты нет.
Замечание. Функция может иметь различные асимптоты при x и x .
|
Пример 5.8. Найти асимптоты кривой: |
|
|
|
||||
|
1. y |
x2 2x 1 |
. |
y |
|
|
|
|
|
x |
у=х+2 |
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
||
|
Решение. |
|
|
|
|
|
||
|
а) Ищем вертикальные |
|
|
|
|
|||
асимптоты: |
|
|
|
|
|
|||
|
|
|
x 2 2x 1 |
|
||||
|
Функция не определена |
|
у= |
|
||||
|
|
x |
||||||
при |
х=0. При |
x+0 |
|
|
||||
у .При x 0, |
у . |
|
|
|
|
|||
0 |
x |
|||||||
Следовательно, прямая х=0 |
||||||||
|
|
|
|
|||||
есть |
вертикальная асимптота |
|
|
|
|
|||
данной кривой. |
|
|
|
|
|
|||
б) Ищем наклонные |
|
Рис. 32 |
|
|
|
|||
асимптоты: |
|
|
|
|
|
|||
k lim |
|
y |
|
lim |
x 2 |
2x 1 |
|
lim |
|
1 |
2 |
|
|
1 |
|
1 . |
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||
x x |
|
x |
|
x |
|
|
|
|
|
0 |
|
|
x |
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||
b |
|
lim |
[ y x] |
lim [ |
|
x 2 |
2x 1 |
. x] |
|
||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim [ |
x 2 2x 1 x 2 |
|
] |
lim |
|
[2 |
1 |
] |
2. |
|
||||||||||||||
|
x |
|
|
|
|
|
x |
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно прямая у=х+2 есть наклонная асимптота данной кривой (рис. 32).
67
Пример 5.9. Найти асимптоты кривой: y e x sin x x.
Решение. 1) Функция всюду определена, вертикальных асимптот нет.
2) Ищем наклонные асимптоты:
|
|
y |
|
|
e x sin x |
|
|
|
k |
lim |
|
|
lim |
|
|
1 |
1. |
|
|
|||||||
|
x x |
|
x x |
|
|
|||
|
|
|
|
|
|
|
|
|
b |
lim [e x sin x x x] |
lim [e x sin x] 0. |
|
x |
x |
Следовательно , прямая у=х есть наклонная асимптота при х + . При х данная кривая асимптот не имеет
5.7. Общий план исследования функции
Полное исследование функций будем поводить, придерживаясь плана:
1)найти область определения функции;
2)найти точки разрыва;
3)отметить простейшие свойства (четность, периодичность, пересечение с осями);
4)асимптоты (вертикальные, наклонные);
5)критические точки первого рода (из условия f (x)=0
или f (x)`- не существует);
6) критические точки второго рода (из условия f (x)=0 или f (x) не существует);
7)интервалы возрастания и убывания;
8)экстремумы;
9)интервалы выпуклости и вогнутости, точки перегиба. На основании проведенного исследования строится гра-
фик функции.
68
Пример 5.10. 1) Исследовать методами дифференциального исчисления функцию у = f (х) и, используя результаты исследования, построить ее график y = x3 / 2 (x+1)2.
Решение. 1. Найдем область определения функции. Поскольку f(x) представляет собой дробь, знаменатель
дроби должен быть отличен от нуля, х+1= 0; х = -1. Таким об-
разом, D (y) =(- , 1)U ( 1, ) .
2. Определяем точки пересечения графика функции с координатными осями. Единственной такой точкой будет точка
О(0,0).
3.Исследуем функцию на четность или нечетность y( x) ( x)3 / 2( x 1)2 x3 / 2(1 x)2.
Очевидно, что у(-х) у (х) и у(-х) -у(х), поэтому функция не является ни четной, ни нечетной.
Рассмотрим периодичность функции. Функция не является периодической.
4. Исследуем функцию на наличие у ее графика асимптот. А. Вертикальные асимптоты.
Вертикальную асимптоту можно искать лишь в виде х = -1. Для доказательства, что эта вертикальная прямая будет
асимптотой вычислим пределы справа и слева при x 1 0, x 1 0 от функции f(x):
lim |
|
x 3 |
= - ; |
lim |
|
x 3 |
= - . |
|
1)2 |
|
1)2 |
||||
x 1 0 2( x |
|
x 1 0 2(x |
|
||||
Поскольку среди найденных пределов получились бесконечности, х= -1 действительно будет вертикальной асимптотой.
Б. Наклонные асимптоты.
Наклонные асимптоты будем искать в виде прямых линий с уравнениями у = kх+ в при x ,x
k = lim |
f ( x) |
lim |
x 2 |
|
|
|
1/2; |
x |
|
1)2 |
|
||||
x |
x 2( x |
|
|
|
|||
|
|
|
|
|
69 |
|
|

|
|
|
|
|
|
|
|
x |
3 |
|
b |
lim ( f ( x) kx) |
lim |
|
|
||||||
|
|
|
||||||||
|
|
2 |
||||||||
|
|
x |
|
|
|
|
2( x 1) |
|||
|
|
|
|
x |
|
|||||
|
|
x 3 |
x 3 2x 2 |
x |
|
|
|
|||
|
lim |
|
|
|
|
|
1. |
|
||
|
|
2 |
|
|
||||||
|
|
|
2( x 1) |
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|||
x 2
Таким образом, прямая с уравнением у=х/2 -1 является асимптотой при x . Те же самые значения пределов для k и b получим и при x , поэтому найденная прямая является асимптотой и при x .
5. Найдем интервалы возрастания, убывания функции,
точки экстремума. Для этого найдем производную функции y .
y = |
3x 2 |
(x 1)2 x 3 2(x 1) |
|
x 2 |
(x 3) |
. |
|
2(x 1)6 |
2(x 1)3 |
||||
|
|
|
|
|||
Критическими точками являются х = 0, х = -3, при которых y = 0 и, х = -1, где производная функции не существует.
При y >0 функция возрастает, при y <0 убывает.
6. Найдем интервалы выпуклости и вогнутости, точки перегиба. Для этого найдем вторую производную
y |
(3x2 |
6x)( x 1)3 (x3 3x2 )3(x 1)2 |
|
|
3x |
. |
|
2 x 1 6 |
(x 1)4 |
||||
|
|
|
|
|||
Точкой, где |
y может менять знак, является точка х = 0, |
|||||
следовательно, х = 0 является точкой перегиба. Если |
y < 0, |
|||||
функция выпукла, при y > 0 - вогнута. |
|
|
|
|
||
7.Результаты исследования знаков производных и соответствующего поведения функции на интервалах оформляем в виде таблицы.
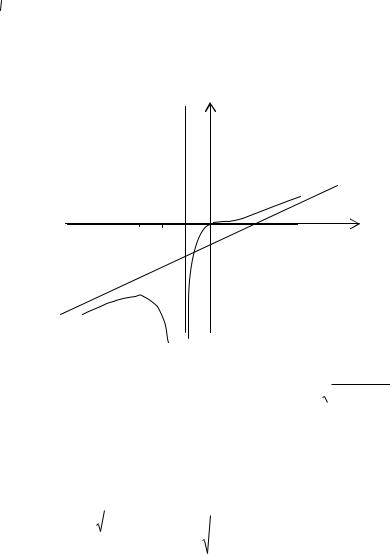
8.Строим график функции, нанося предварительно асимптоты, точки пересечения графика с координатными осями, точки экстремума и перегиба графика и соединяя их плавной кривой (рис. 33 ).
70
|
|
|
|
|
|
|
Таблица 2 |
||
x |
|
-,-3 |
-3 |
-3,-1 |
-1 |
-1,0 |
0 |
0,∞ |
|
|
|
+ |
0 |
|
Не сущ. |
+ |
0 |
+ |
|
f |
(x) |
|
|||||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
Не сущ. |
|
0 |
+ |
|
(x) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
f(x) |
Возр., |
Max y= |
убыв., |
Не сущ. |
возр., |
Точка |
Возр. |
|
|
|
|
вып. |
=-27/4 |
вып. |
|
вып. |
перег. |
Вогн. |
|
y
-3 |
-1 |
0 |
|
x
Рис. 33
Пример 5.11..Исследовать функцию y 3 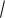 2x 2 x3 и построить график.
2x 2 x3 и построить график.
1.Функция всюду определена: x R
2.Общего вида. Точки пересечения с осями
x2 (2 x) 0 : x 0, |
x 2, т.е. (0,0), (2,0) . |
3. Вертикальных асимптот нет. Ищем наклонные:
3 |
2x2 x3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
k lim |
|
|
lim 3 |
|
1 |
1, |
||
|
x |
x |
||||||
x |
x |
|
|
|
||||
71

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2 x3 x3 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
b |
|
|
lim |
|
|
|
|
2x |
|
|
x |
|
|
x |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
x3 2x2 x3 |
x2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
4 |
|
4x |
5 |
x |
6 |
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x6 4x |
|
|
|
|
|
3 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Функция имеет наклонную асимптоту у= х+2/3. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4. Ищем критические точки первого рода. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
4x 3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
4 3x |
|
|
|
|
|
|
|
|
x1 |
0, x2 2, x3 4 / 3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
3 x 4 (2 x)2 |
|
|
3 3 x(2 x) 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5. Ищем критические точки второго рода. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
x(2 x)2 |
(4 3x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[(2 x)2 x2(2 x)] |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 x 2 (2 x)4 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|||||||||||||||||||||||||
y 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x 2 (2 x)4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
1 93 |
|
x3 |
(2 x)6 |
(4 3x)(2 x)[2 x 2x] |
|
9x(2 x) (4 3x)(2 3x) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x4 (2 |
x)8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93 x4 (2 x)5 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
18x 9x2 8 12x 6x 9x |
2 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
, |
|
x |
0, x |
2. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
93 x4 (2 x)5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93 x4 |
(2 x)5 |
1 |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|||||
х |
|
, 0 |
|
0 |
|
|
|
|
|
|
0,4/3 |
|
4/3 |
|
|
|
|
|
|
|
|
|
|
4/3,2 |
|
|
2 |
|
|
2, |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
н.с. |
|
|
|
+ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н.с. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
н.с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
т.п. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
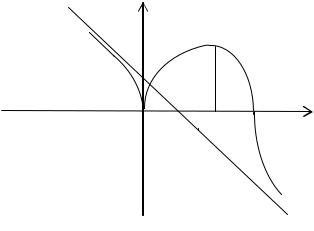
6. На основании вышеизложенного строим график. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y
|
4/3 |
2 |
x |
|
0 |
||||
|
Рис. 34
Вопросы для самопроверки
1.Сформулируйте определение возрастающей и убывающей на отрезке функции. Приведите достаточный признак возрастания функции.
2.Дайте определение точки экстремума функции.
3.Сформулируйте правило для отыскания экстремума функции.
4.Приведите пример, показывающий, что обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума функции.
5.Как найти наибольшее и наименьшее значения функции, дифференцируемой на отрезке?
6.Сформулируйте определения выпуклости и вогнутости линии. Точки перегиба. Как находятся интервалы выпуклости
ивогнутости и точки перегиба?
7.Дайте определение асимптоты линии. Как находятся вертикальные и наклонные асимптоты?
8.Изложите схему общего исследования функции и построения ее графика.
73
