
- •1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •1.1.1. Понятие функции
- •1.1.2. Способы задания функций
- •1.1.4. Классификация функций
- •2.1. Предел функции
- •2.2. Бесконечно большая и ограниченная функции
- •2.3. Бесконечно малые и их основные свойства
- •Вопросы для самопроверки
- •3.6. Производные элементарных функций
- •Правила дифференцирования
- •Уравнения (3.9) называются параметрическими уравнениями кривой, а t – параметром.
- •Вопросы для самопроверки
- •Замечание 2. Если производная существует не во всех точках внутри [a,b], то утверждение может оказаться неверным, т.е. на отрезке может не оказаться точки в которой производная обращается в нуль. Например:
- •4.2. Теорема Лагранжа
- •Приведем теорему о конечных приращениях.
- •Теорема Лагранжа. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема во всех внутренних точках отрезка, то внутри отрезка [a,b] существует по крайней мере одна точка c, a<c<b, что
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •6.1. Предельные показатели в микроэкономике
- •6.2. Максимизация прибыли
- •8.4. Интегрирование с помощью замены переменной
- •Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
- •11.12.5. Оптимизация спроса
- •12.1. Основные понятия и определения
- •Теорема. Если в уравнении
- •Определение. Общим решением дифференциального уравнения первого порядка называется функция
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •11.12.5. Оптимизация спроса…………………………174
- •12.1. Основные понятия и определения…………………177
- •12.11.4. Неоклассическая модель роста……………..214
|
z |
|
|
L2 |
Р |
L1 |
|
|
|
||
|
|
|
у |
x0 |
M0 |
y0 |
|
|
|
||
х |
|
|
|
Рис. 55
Замечание. Для функции у = f(x) существование производной f (x0) гарантирует непрерывность функции f(x) в точке х =х0. Для функции n 2 переменных из существования частных производных по всем переменным в точке М0 не следует непрерывность функции u= f(М) в этой точке.
11.4. Полное приращение функции и полный дифференциал
Рассмотрим функцию двух переменных f (x,у). Пусть она определена и непрерывна в точке М0(х0 ,у0) и некоторой ее окрестности. Перемещению из точки М0(х0 ,у0) в точку М(х ,у)
х = x0+ x, у = у0+ у соответствует полное приращение
функции: z = f (М) - f (М0) = f (x0+ x, у0+ у) - f (x0, у0),
т.к. здесь, вообще говоря, все переменные получают приращения, отличные от нуля.
В общем случае, для произвольной функции, полное приращение имеет сложную структуру. Однако для широкого класса функций z = f (x, у), называемых дифференцируемыми, полное приращение z можно приближенно выразить линейно через приращения аргументов.
Обозначим через расстояние между точками М0 и М:
150

= 
 x2 y 2 . Очевидно, что 0 х 0 и у 0.
x2 y 2 . Очевидно, что 0 х 0 и у 0.
Функция z = f (x, у) называется дифференцируемой в точке М0 (х0,у0), если существуют числа А и В такие, что пол-
ное приращение функции представимо в виде: |
|
z = А x + В y + , где 0 при 0 |
(11.4) |
Определение. Линейная функция А x + В y |
перемен- |
ных x и y называется полным дифференциалом функции f (x, у) в точке М0 (х0,у0) и обозначается
dz = А x + В y.
Следовательно, формулу (11.4) можно записать
z = dz +.
Замечание. Формулу (11.4) можно записать в другом ви-
де: z = А x + В y + x + y,
где 0 и 0 при х 0 и у 0.
Установим связь между дифференцируемостью функции и существованием у нее частных производных.
Теорема 1. (Необходимое условие). Если функция
z = f (x, у) дифференцируема в точке М0 (х0,у0), то эта функция имеет в точке М0 частные производные, причем
f (x |
0 |
, y |
0 |
) =А, |
f (x |
0 |
, y |
0 |
) =В. |
x |
|
|
y |
|
|
Следовательно, полный дифференциал можно записать в виде:
dz = |
z |
x + |
z |
y. Но x =d х и y= dу. |
||
|
y |
|||||
|
x |
|
|
|
||
Поэтому dz = |
f (x, y) dx + f (x, y) |
dy (в произвольной |
||||
|
|
|
|
x |
y |
|
точке М(х, у). Таким образом, dz = |
dx z + |
d y z - полный диф- |
||||
ференциал равен сумме частных дифференциалов. Теорема 2. (Достаточное условие). Если функция
z = f (x, у) имеет частные производные в точке М0 (х0, у0) и в некоторой ее окрестности, и эти частные производные являются непрерывными функциями, то эта функция дифференцируема в точке М0 , причем
dz = |
f (x |
0 |
, y |
0 |
) х + |
f (x |
0 |
, y |
0 |
) у. |
|
x |
|
|
y |
|
|
151
Теорема 3. Если функция f (x, у) дифференцируема в точке М0, то она непрерывна в этой точке.
Замечание. Слагаемое есть бесконечно малая высшего порядка малости по сравнению с х и у. Поэтому диффе-
ренциал – главная линейная часть приращения функции.
11.5. Частные производные и дифференциалы высших порядков
Пусть дана функция z = f (x,y). Найдем ее частные производные:
z |
f ( x, y) и |
z |
f ( x, y) . |
x |
x |
y |
y |
|
|
Частные производные, в свою очередь, являются функциями двух переменных: х и у. Их можно снова дифференцировать по этим переменным. Частные производные от частных производных первого порядка называются частными производными второго порядка и обозначаются следующим образом:
2 z |
|
z |
f |
( x, y) ; |
2 z |
|
|
z |
f |
( x, y) ; |
||||
|
|
|
|
|
|
|
|
|
||||||
x 2 |
|
|
xx |
|
x y |
|
|
|
xy |
|
||||
x |
x |
|
|
|
y |
x |
|
|
||||||
|
2 z |
|
|
z |
|
|
2 z |
|
|
|
z |
|
|
||||
|
|
|
|
|
|
|
f |
(x, y) ; |
|
2 |
|
|
|
|
f |
(x, y) . |
|
|
|
|
|
|
|
|
|||||||||||
|
y x |
|
|
|
|
|
yx |
|
y |
|
|
|
|
|
yy |
|
|
|
|
x |
y |
|
|
|
|
y |
y |
|
|
||||||
Производные |
f |
(x, y) , f |
(x, y) , отличающиеся порядком |
||||||||||||||
|
|
|
|
|
|
yx |
|
xy |
|
|
|
|
|
|
|
|
|
дифференцирования называются смешанными производными второго порядка.
Пример 11.8. Найти производные второго порядка функции z x4 x5 y3 y3 16.
Решение.
z |
4x 3 5x 4 y 3 ; |
z |
3x5 y 2 3y 2 ; |
|
x |
y |
|||
|
|
|||
|
|
|
152 |
2 z |
12x 2 20x 3 y 3 ; |
2 z 6x5 y 6 y ; |
||
x 2 |
|
y 2 |
|
|
2 z |
15x 4 y 2 ; |
|
2 z |
15x 4 y 2 . |
x y |
|
y x |
||
|
|
|
||
Оказалось, что смешанные производные второго порядка равны.
Теорема. Смешанные производные второго порядка равны в той области, где они непрерывны
2 z |
= |
2 z |
. |
|
y x |
x y |
|||
|
|
Частные производные от частных производных второго порядка называются частными производными третьего порядка и обозначаются
3 z |
|
|
|
2 z |
|
3 z |
|
|
|
2 z |
|
3 z |
|
|
|
2 z |
|
|
||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
и |
x |
3 |
|
|
|
x |
2 |
|
|
y |
3 |
|
|
|
y |
2 |
|
|
x |
2 |
y |
|
|
|
y x |
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
x |
|
|
||||||||||
т.д.
Введем понятие дифференциала второго и более высоких порядков.
Пусть функция z= f (х, у). Имеет непрерывные частные производные достаточно высоких порядков. Рассмотрим дифференциал этой функции.
dz f (x, y)dx + |
f (x, y)dy . |
(11.5) |
x |
y |
|
Этот дифференциал называется полным дифференциа-
лом первого порядка, он зависит, во-первых от х и у, т.к. от х и у зависят частные производные, во-вторых, он зависит от
dx = x и dy = y. Эти величины не зависят от х и у. Поэтому при дифференцировании по х или у их можно считать постоянными.
153

Полный дифференциал от полного дифференциала пер-
вого порядка называется полным дифференциалом второго
порядка и обозначается d 2 z d dz . |
|
|
|
|
|
|||
d 2 z d z dx z dy = |
|
|
|
|
|
|
||
x |
y |
|
|
|
|
|
|
|
= ( f (x, y)dx + f |
(x, y)dy) dx + |
( f (x, y)dx + |
f |
(x, y)dy) |
dy = |
|||
x |
y |
x |
x |
|
y |
|
y |
|
= [ f (x, y)dx + f |
(x, y)dy]dx +[ f |
(x, y)dx |
+ f |
(x, y)dy]dy . |
||||
xx |
yx |
|
xy |
|
|
yy |
|
|
Таким образом |
|
|
|
|
|
|
|
|
d 2 z f (x, y)dx2 +2 f |
(x, y)dxdy + f |
(x, y)dy2 . |
|
|||||
xx |
|
xy |
|
|
yy |
|
|
|
11.6. Экстремум функции нескольких переменных. Необходимое условие экстремума
Рассмотрим функцию z= f(x,y), непрерывную в точке М0(x0,y0) и некоторой ее окрестности.
Точка М0(x0,y0)) называется точкой максимума функции z = f(М) (рис. 75), если всюду в некоторой окрестности точки М0 (0< d (M0 M) < ) выполняется неравенство
f (М) <f (М0) или z = f (М) – f (М0) <0.
Точка М0 (x0,y0) называется точкой минимума функции z=f(М) (рис.76), если всюду в некоторой окрестности точки М0
(0< d (M0M) < ) выполняется неравенство |
|
|||
|
|
z |
z |
|
|
f(M) |
f(M0) |
f(M) |
|
|
|
|
||
|
|
|
|
f(M0) |
|
|
y0 |
|
y0 |
x0 |
|
y |
x0 |
y |
|
M0 |
M0 |
||
|
x |
x |
||
|
|
|
||
Рис.1356. |
Рис. 57 |
|
|
|
154 |
f (М) f (М0) или z = f (М) – f (М0) 0.
Точки максимума и точки минимума – точки экстремума. Понятие экстремума носит локальный характер: в определении рассматриваются лишь точки М1 достаточно близкие к точке
М0.
Теорема. (Необходимое условие). Если функция z= f(x,y)
дифференцируема в точке М0(x0,y0) и имеет в этой точке экстремум, то
f (x |
0 |
, y |
0 |
) 0 ; |
f (x |
0 |
, y |
0 |
) 0 . |
x |
|
|
y |
|
|
Следствие. В тех точках, в которых существуют частные производные и хотя бы одна из них отлична от нуля, экстремума быть не может.
Значит, экстремум следует искать только в тех точках, в которых все частные производные первого порядка равны нулю, либо хотя бы одна из них не существует.
Такие точки называются критическими (стационарными). В критической точке экстремум может быть, а может и не быть. В общем случае о наличии или отсутствии экстремума в критической точке судят с помощью достаточных признаков экстремума.
11.7. Достаточный признак экстремума
Теорема. Пусть функция z= f(х, у) имеет все непрерывные частные производные до второго порядка включительно в некоторой окрестности точки М0 (х0 ,у0), а в самой точке М0
|
(x0 |
, y0 ) 0 ; |
|
|
, y0 ) 0 |
(т.е. точка М0 |
является критиче- |
||||||||||||
f x |
|
f y (x0 |
|||||||||||||||||
ской). Обозначим: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f |
(x |
0 |
, y |
0 |
) A , |
f |
(x |
0 |
, y |
0 |
) B , |
f |
(x |
0 |
, y |
0 |
) C . |
|
|
xx |
|
|
|
xy |
|
|
|
yy |
|
|
|
||||||
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1. |
Если число = AC B2 >0, то точке М0 (х0 ,у0) функ- |
||||||||||||||||
ция f(х, у) имеет экстремум, а именно максимум, если А < 0 и минимум, если А > 0.
155

2.Если число = AC B2 <0, то точке М0 (х0 ,у0) экстремума нет.
3.Если число = AC B2 =0, то признак не применим.
Пример 11.9. Найти экстремум функции z x3 y 3 9xy 27 .
Решение. Найдем частные производные и приравняем их нулю.
z |
|
|
2 |
|
|
|
|
|
|
3x |
|
9 y 3x 2 |
9 y 0 |
|
|
x |
|
. |
|||||
z |
|
3y 2 |
|
3y 2 |
9x 0 |
||
|
9x |
|
|||||
y |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решая систему уравнений, получим критические точки
х1=0; у1 =0; х2= 3; у2= 3; М1(0,0); М2(3,3).
Найдем вторые производные:
2 z |
= 6х, |
2 z |
= 9, |
2 z |
= 6у. |
||
x 2 |
x y |
y 2 |
|||||
|
|
|
|||||
В точке М1: А=0, |
В= 9, С =0. AC B2 < 0. Экстремума |
||||||
нет. |
|
|
|
|
|
|
|
В точке М2: А=18, |
В = 9, |
С = 18. |
AC B2 >0. Следова- |
||||
тельно, в точке М2 функция имеем минимум, так как А0.
zmin 27 27 81 27 0.
11.8.Наибольшее и наименьшее значение функции в замкнутой области
Пусть функция z=f(x,y) непрерывна в замкнутой области D . Тогда в области D найдётся хотя бы одна точка A(x0,y0), в которой функция принимает своё наибольшее значение M: f(x0,y0) = M и найдется хотя бы одна точка B(x1,y1), в которой
156

функция принимает своё наименьшее значение m: f(x1,y1) = m, т.е.
f(x,y) M и f(x,y) m, |
(11.6) |
для любых точек области D.
Возможны два случая. Точка А лежит внутри области D или точка А лежит на границе. То же самое и относительно точки В. Если А и В лежат внутри области, то они, в силу неравенств (11.17), совпадают с экстремальными точками.
Таким образом, для нахождения наибольшего и наименьшего значений необходимо:
1)найти все критические точки, попадающие внутрь области D и вычислить значения функции в этих точках;
2)найти критические точки на границе области и вычислить в них значения функции;
3)выбрать наибольшее и наименьшее из всех полученных чисел.
11.9. Производная по направлению
Пусть дана дифференцируемая функция трёх независимых переменных:
|
u=f(x, y, z). |
|
|
|||
Частные производные |
u |
, |
u |
, |
u |
характеризуют ско- |
x |
y |
|
||||
z |
||||||
рость изменения функции в направлении координатных осей. Можно рассматривать более общую задачу: найти скорость изменения функции в произвольном направлении l0, не совпадающем с направлением координатной оси.
Возьмём в пространстве некоторую точку М0(x0,y0,z0) и
через неё проведём прямую параллельную l0 . Возьмём на прямой другую точку М1(х0+ x, y0+ y, z0+ z) на расстоянии
|
x2 y 2 z 2 |
(11.7) |
от точки М0 (рис. 58).
157
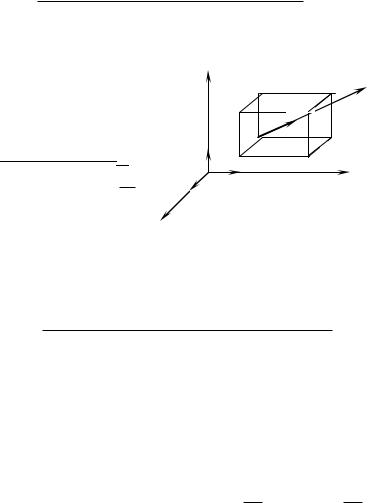
|
При переходе из точки М0 |
в точку М1 функция u=f(M) |
|
|||||||||||||
получит полное приращение u= f(M1) f(M0). Отношение |
|
|||||||||||||||
|
|
u |
|
f (x0 x, y0 y, z0 z) f (x0 , y0 , z0 ) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
есть средняя скорость изменения функции u= f(M) в направле- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нии, указанным вектором l0 . |
|
|
|
|
|
|
|
|
||||||||
|
Определение. |
Предел |
|
|
z |
|
|
|
|
|||||||
этого выражения, если он су- |
|
|
|
|
M1 |
|
|
|||||||||
ществует, |
называется |
произ- |
|
|
|
|
|
l |
||||||||
|
|
|
|
|
|
|||||||||||
водной функции u = f(M) |
в |
|
|
y |
M0 |
|
|
|||||||||
|
|
l0 |
z |
|||||||||||||
точке М0 по направлению l . |
|
|
k |
|
|
|
||||||||||
|
|
|
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ul |
|
|
|
|
j |
|
|
|
||
|
Обозначается: |
; |
; |
|
i |
|
|
y |
|
|||||||
|
l |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Рис. 58 |
|
|
||
ul ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, по определению: |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
u lim |
u |
или |
|
|
|
(11.8) |
||||
|
|
|
|
|
|
l |
|
0 |
|
|
|
|
|
|
|
|
|
u |
|
lim |
u(x0 x, y0 y, z0 z) f (x0 , y0 , z0 ) |
|
|||||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
Производная по направлению характеризует скорость |
|||||||||||||||
изменения функции в данном направлении. |
|
|
|
|
||||||||||||
|
Установим связь между производной по направлению и |
|||||||||||||||
частными производными. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть вектор l0 |
задан координатами: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l0 cos , cos , cos . |
|
|
|
|
|
|
|
|
|
|
||||||
|
Из |
|
рисунка |
видно, |
что |
cos |
x ; |
cos |
y ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos z |
- направляющие косинусы. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем полное приращение функции u в виде |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
158 |
|
|
|
|
|
|
u f (M1 ) f (M 0 ) |
|
|
|
|
|
||||
u x |
u y u z 1 x 2 y 3 z , |
|
|
||||||
x |
|
y |
z |
|
|
|
|
|
|
где 1 , 2 , 3 |
0 при |
x 0, y 0, z 0 (свойство диф- |
|||||||
ференцируемости функции). |
|
|
|
|
|
||||
Разделим обе части равенства на |
|
|
|
||||||
u |
u x |
u y u z |
1 |
x 2 |
y |
3 z . |
|
||
|
x |
y |
z |
|
|
|
|
|
|
Если |
|
0 |
то |
из |
(11.7) |
следует, |
что |
||
x 0, y 0, z 0 , |
т.е. 1 , 2 , 3 |
0 . |
Перейдём в |
обеих |
|||||
частях равенства к пределу при 0 . Правая часть равенства имеет предел и этот предел равен:
|
lim |
u u cos u cos u cos . |
|
|
|||
|
0 |
|
x |
y |
z |
|
|
Значит, |
существует и предел левой части lim |
u |
u . |
||||
|
|
|
|
|
0 |
|
l |
Таким образом, получим следующую формулу |
|
|
|||||
|
u |
|
u cos u cos u cos . |
|
(11.9) |
||
|
l |
|
x |
y |
z |
|
|
Данная |
формула |
выражает |
производную |
функции |
|||
|
|
|
|
|
cos , cos , cos через |
||
u=f(x,y,z) по любому направлению l0 |
|||||||
производные этой функции по трём взаимно перпендикуляр-
ным направлениям i , j, k .
В случае функции двух переменных u = f (x,y) имеем:
l |
cos , cos |
и u u cos u |
|||
0 |
|
|
l |
x |
y |
|
|
|
|||
|
u |
|
u cos |
u sin |
|
|
l |
|
x |
|
y |
cos или |
|
|
|
(т.к. |
|
). |
(11.10) |
|
2 |
|
|
159

Пример 11.24. Найти производную функции f(x,y)=x y2 в точке М0 (5;1) по направлению к точке М1 (9;4).
Решение. Направляющие косинусы вектора M 0 M 1
M 0 M1 = 4,3 ; |
|
|
|
|
|
|
|
|
|
|
16 9 5 , |
||||||||
M 0 M1 |
|||||||||
cos |
|
4 |
;sin |
|
3 |
. |
|
||
5 |
5 |
|
|||||||
|
|
|
|
|
|||||
Найдем значения частных производных в точках
f |
y 2 |
|
1; |
f |
2xy |
|
10. |
|
|
||||||
x |
|
|
M 0 |
y |
|
|
M 0 |
|
|
|
|
|
|
|
По формуле (11.10) получим:
f |
1 |
4 |
10 |
3 |
|
34 |
. |
|
x |
5 |
5 |
|
5 |
||||
|
|
|
|
|
||||
11.10. Градиент функции. Свойства градиента
Пусть в пространстве задана функция трёх переменных u=f(x,y,z). Тогда в некоторой точке M0(x0,y0,z0) имеется бесчисленное множество различных направлений и дифференцируемая в точке М0 функция в этой точке имеет бесчисленное множество производных, соответствующих различным направлениям.
Во многих задачах при изучении поведения функции в данной точке пространства наибольший интерес представляет вопрос о направлении быстрейшего возрастания функции в точке. Это направление задаётся специальным вектором – градиентом.
Пусть функция u=f(x,y,z) имеет в точке M0(x0,y0,z0) непрерывные частные производные. Тогда в точке М0 можно по-
строить вектор с координатами:
|
f (x , y |
|
, z ) |
; |
f (x , y |
|
, z ) |
; |
f (x , y |
|
, z |
|
) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
. |
||
|
x |
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
160 |
|
|
|
|
|
|
|
Началом этого вектора служит точка М0, в которой вычислены частные производные. Этот вектор называется градиентом скалярной функции в данной точке и обозначается
grad u(M 0 ) или grad f (x0 , y0 , z0 ) (рис. 59).
Таким образом,
gradu(M ) |
u |
|
u |
|
u |
(11.11) |
i |
j |
k . |
||||
|
x |
|
y |
|
z |
|
Аналогично определяется градиент функции двух переменных u=f(x,y). Это – вектор на плоскости Oxy:
|
|
|
|
|
|
grad u(M ) |
u |
u |
|
|
|
|
(11.12) |
|||||||
|
|
|
|
|
|
x |
i |
j . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||
|
|
Пример 11.10. Найти градиент функции u x2 |
y 2 z 2 |
|||||||||||||||||
в точке М1 (2,1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решение. grad u(M ) |
2xi 2 yj |
; grad |
u(M1 ) 4i |
|
2 j . |
|||||||||||||
l |
|
Возьмём |
в |
точке |
|
М0(x0,y0,z0) |
единичный |
вектор |
||||||||||||
cos , cos , cos (рис. |
59) |
и запишем производную от |
||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции u=f(x,y,z) по направлению l0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
u |
u cos |
|
u cos u cos . |
|
|
||||||||||
|
|
|
|
|
l |
x |
|
|
y |
|
|
z |
|
|
|
|||||
|
|
Видим, что производную по направлению можно запи- |
||||||||||||||||||
сать в виде: u l |
, gradu(M |
0 |
) |
|
|
|
|
|
z |
|
|
|||||||||
|
|
|
|
|
l |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad |
|
||
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
gradu(M 0 ) |
|
cos или |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
l |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
M0 |
|
|||||||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
l0 |
||||
пр l gradu(M 0 ) |
|
|
|
|
|
|
|
|
|
|||||||||||
(11.13) |
|
|
x |
|
|
|
|
y |
||||||||||||
l |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 59 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, производная скалярной функции u= f (M) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
точке М0 в |
направлении |
l0 |
равна |
|
|
проекции |
вектора |
||||||||||||
gradu(M 0 ) на направление вектора l0 . 161

Из формулы (11.13) следует, что производная скалярной функции в точке М0 имеет наибольшее значение в направлении градиента функции в той же точке, т.к. в этом случае
0 и cos 0 1.
Вэтом случае формула (11.13) будет иметь вид:
u |
|
|
|
|
|
u 2 |
|
u |
2 2 |
|
|
|
|
gradu(M |
|
) |
|
|
|
|
|
- |
(11.14) |
|
|
|
0 |
|
|
|
|
|
|
||
l |
|
|
|
|
|
|
x |
|
y |
|
|
это наибольшая скорость возрастания функции. Следовательно, модуль градиента равен наибольшей ско-
рости возрастания функции в данной точке.
Из формулы (11.13) следует, что производная по направ-
лению, перпендикулярному градиенту ( 2 ) равна нулю,
т.е. в этом направлении функция не изменяется.
Пользуясь рассмотренным свойством, можно дать другое определение градиента, не связанное с выбором системы координат.
Определение. Градиентом функции u=f(x,y,z) в точке М0(x0,y0,z0) называется вектор, в направлении которого производная имеет наибольшее значение. Длина вектора градиента равна максимальному значению производной в данной точке.
Рассмотрим функцию двух переменных u= u(x,y)
grad u u , u .x y
Линии в плоскости аргументов Оху, для которых функция u(x,y) сохраняет постоянные значения, называется линией уровня. Её уравнение: u(x, y) = c.
Градиент функции u(x,y) в любой точке М, перпендикулярен к линии уровня функции, проходящей через данную точку. В пространстве градиент направлен по нормали к поверхности уровня функции u=f(x,y,z), проходящей через данную точку.
162
11.11. Получение функции на основании экспериментальных данных по методу наименьших квадратов
Пусть на основании эксперимента требуется установить функциональную зависимость величины у от величины х:
у = (х).
Пусть в результате эксперимента получено n значений функции у при соответствующих значениях аргумента. Результаты записаны в таблицу:
|
|
|
|
Таблица 4 |
|
х |
х1 |
х2 |
. . . |
|
хn |
|
|
|
|
|
|
у |
у1 |
у2 |
. . . |
|
уn |
|
|
|
|
|
|
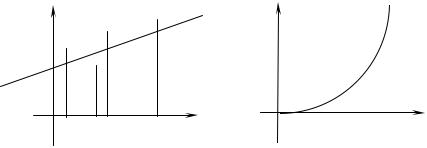
Вид функции у = (х) устанавливается или из теоретических соображений, или на основании расположения на координатной плоскости точек, соответствующих экспериментальным значениям. Пусть, например, экспериментальные точки расположены на координатной плоскости так, как изображено на рис. 60. Учитывая, что при проведении эксперимента имеют место погрешности, естественно предположить, что искомую функцию у = (х) можно искать в виде линейной функции
y = ax + b. Если экспериментальные точки расположены так, как указано на рис. 61, то естественно искать функцию
у = (х) в виде у=а x b и т.д.
у |
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
х1 |
х2 |
х3 |
х |
n x |
|
x |
0 |
|||||||
|
|
Рис. 60 |
|
|
|
Рис. 61 |
|
|
|
|
|
|
|||
163
При выбранном виде функции у = (х,a,b,c,...) остается подобрать входящие в нее параметры a, b, c, ... так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.
Широко распространенным методом решения данной за-
дачи является метод наименьших квадратов. Этот метод за-
ключается в следующем.
Рассмотрим сумму квадратов разностей значений уi, даваемых экспериментом, и функции (х,a,b,c,...) в соответствующих точках:
n |
|
(x , a,b, c,...)]2 . |
|
S(a,b, c,...) [ y |
i |
(11.15) |
|
i 1 |
i |
|
|
|
|
|
|
Подбираем параметры a, b, c, ... так, чтобы эта сумма |
|||
имела наименьшее значение |
|
|
|
n |
|
(xi , a, b, c,...)]2 min . |
|
S(a, b, c,...) [ yi |
|||
i 1 |
|
|
|
Итак, задача свелась к нахождению значений параметров |
|||
a, b, c, ..., при которых функция S(a, b, c,...) |
имеет минимум. |
||
Эти значения a, b, c, ... удовлетворяют системе уравнений
S |
0, |
S |
0, |
a |
|
b |
|
или в развернутом виде:
n
[ yi (xi
i 1
n
[ yi (xi
i 1
n
[ yi (xi
i 1
,a,b, c,...)]
,a,b, c,...)]
,a,b, c,...)]
(xi , a,b, c,...)
a
(xi , a,b, c,...)
b
(xi , a,b, c,...)
c
S |
0, ... |
c |
|
0 , |
|
0 , |
(11.16) |
0 . |
|
Здесь имеется столько уравнений, сколько и неизвестных. В каждом конкретном случае исследуется вопрос о существовании решения системы уравнений (11.16) и о существовании минимума функции S(a, b, c,...).
164
Рассмотрим несколько случаев определения функции у= (х,a,b,c,...).
1. Пусть y=ax+b. Функция S (a, b ) в этом случае имеет
вид
|
|
S(a,b) |
n |
|
|
(ax b)]2 . |
|
|||
|
|
[ y |
i |
(11.17) |
||||||
|
|
|
|
i 1 |
|
i |
|
|
||
|
|
|
|
|
|
|
|
|
||
Это функция с двумя переменными a и |
b (хi , y i – задан- |
|||||||||
ные числа). Следовательно, |
|
|
|
|
|
|
||||
|
|
S 2 [ y (ax b)]x 0, |
|
|||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
a |
i 1 |
i |
|
i |
|
i |
|
|
|
|
|
|
|
|
|
||||
|
|
S |
n |
|
|
|
|
|
|
|
|
|
2 [ yi |
(axi |
b)] 0, |
|
|||||
|
|
b |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. система уравнений (1.27) в этом случае принимает вид |
||||||||||
n |
|
|
n |
2 |
|
|
n |
|
|
|
yi |
xi a xi |
|
b xi 0, |
|
|
|||||
i 1 |
n |
|
i 1 |
|
|
i 1 |
|
|
(11.18) |
|
|
|
n |
|
|
|
|
|
|
||
|
yi a xi |
bn 0. |
|
|
|
|||||
|
|
|
|
|||||||
|
i 1 |
i 1 |
|
|
|
|
|
|
|
|
Получили систему двух линейных уравнений с двумя неизвестными a и b. Очевидно, что система имеет определенное решение, и что при найденных значениях a и b функция S (a, b) имеет минимум.
2. Пусть за аппроксимирующую функцию взят трехчлен второй степени
yax2 bx c .
Вэтом случае выражение (1.27) имеет вид
n |
|
(ax 2 |
bx c)]2 . |
S(a,b, c) [ y |
i |
||
i 1 |
i |
i |
|
|
|
|
Это функция трех переменных a, b, с. Система уравнений (11.18) принимает вид
165
n |
2 |
|
2 |
0, |
||
|
|
[ yi (axi |
bxi c)]xi |
|||
i 1 |
|
|
|
|||
|
n |
2 |
bxi c)]xi |
0, |
||
|
[ yi (axi |
|||||
i 1 |
|
|
|
|||
|
|
n |
2 |
|
|
|
[ yi (axi |
bxi c)] 0, |
|||||
|
|
|||||
|
i 1 |
|
|
|
||
или в развернутом виде
n |
2 |
n |
4 |
|
|
yi xi |
a xi |
||
i 1 |
|
i 1 |
|
|
|
n |
|
n |
3 |
|
yi xi |
a xi |
|
|
i 1 |
|
i 1 |
|
|
|
|
n |
n |
|
|
yi a xi |
|||
|
|
|||
|
|
i 1 |
i 1 |
|
|
n |
|
3 |
n |
2 0, |
b xi |
c xi |
||||
|
i 1 |
|
|
i 1 |
|
|
n |
2 |
n |
|
|
b xi |
c xi |
0, |
|||
|
i 1 |
|
|
i 1 |
|
2 |
n |
|
|
|
|
b xi cn 0. |
|||||
|
i 1 |
|
|
|
|
Получаем систему линейных уравнений для определения неизвестных a, b, с. Из характера задачи следует, что система имеет определенное решение, и что при полученных значениях a, b, с функция S(a, b, c) имеет минимум.
Пример 11.11. Пусть на основании эксперимента получены четыре значения искомой функции у= (х) при четырех значениях аргумента (n= 4), которые записаны в таблице:
Таблица 5
|
х |
1 |
2 |
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
3 |
4 |
|
2,5 |
0,5 |
|
|
|
|
|
|
|
|
|
|
|||
Решение. Будем искать функцию в виде линейной |
|||||||||
функции y=ax+b. Составляем выражение S(a, b) : |
|||||||||
|
|
|
|
|
|
4 |
|
|
(ax b)]2 . |
|
|
|
|
S(a,b) [ y |
i |
||||
|
|
|
|
|
|
i 1 |
i |
||
|
|
|
|
|
|
|
|
|
|
Чтобы составить систему (11.18) для определения коэффициентов a и b предварительно вычисляем
4 |
21, |
4 |
2 |
39, |
4 |
11, |
4 |
|
10. |
y x |
x |
x |
y |
i |
|||||
i i |
|
i |
|
|
i |
|
|
|
|
i 1 |
|
i 1 |
|
|
i 1 |
|
i 1 |
|
|
166

Система (11.18) принимает вид 21 39a 11b 0,
10 11a 4b 0.
Решая эту систему, находим a и b: a =- 26/35, b = 159/35.
Искомая прямая (рис. 62) есть y 2635 x 15935 .
у
|
|
|
|
|
|
(х,a,b)
у1
х
Рис. 62
11.12. Функции нескольких переменных в задачах экономики
Рассмотрим некоторые типичные задачи нахождения экстремума функции нескольких переменных, возникающие в экономике.
11.12.1. Прибыль от производства товаров разных видов
Пусть x1, x2 , , xm количество производимых |
m разно- |
|
видностей товара, а их цены – соответственно P , P , , P |
(все |
|
1 2 |
m |
|
Pi постоянные величины). Пусть затраты на производство этих товаров задаются функцией издержек
167

C S x1 , x2 , , xm .
Тогда функция прибыли имеет вид |
|
|
|
|
|
|||||
P x |
P x |
2 |
P x |
m |
S x , x |
2 |
, , x |
m |
. |
(11.19) |
1 1 |
2 |
m |
1 |
|
|
|
||||
Максимум прибыли естественно искать как условие локального экстремума функции многих переменных при xi 0 (при отсутствии других ограничений):
0, i 1,2, , m.
xi
Это условие приводит к системе алгебраических уравнений относительно переменных xi
Pi S 0, i 1,2, , m. (11.20)xi
Система уравнений (11.20) реализует известное правило экономики: предельная стоимость (цена) товара равна предельным издержкам на производство этого товара. Решениями этой системы уравнений являются наборы, состоящие из m значений каждый. Нужно заметить, что сам процесс нахождения решения системы уравнений (11.20) зависит от вида функции издержек и может быть достаточно сложным.
Найденные наборы значений x10 , x20 , , xm0 необходимо
проверить по достаточному признаку локального максимума. Иными словами, нужно выполнить следующие операции:
а) составить гессиан для функции вида (11.19):
|
S |
S |
S |
|
|
||
|
|
|
|||||
|
x1x1 |
x1x2 |
|
x1xm |
|
|
|
|
S |
S |
S |
|
|
||
H m |
x2 x1 |
x2 x2 |
|
x2 xm |
. |
(11.21) |
|
|
|
|
|
||||
|
|
|
|||||
|
S |
S |
S |
|
|
||
|
xm x1 |
xm x2 |
|
xm xm |
|
|
|
Если знаки главных миноров этого определителя чередуются, начиная со знака «минус», то проверяемое решение
x10 , x20 , , xm0 системы уравнений (11.20) является m – мерной точкой локального максимума функции прибыли (11.19);
168
б) далее, необходимо выбрать из этих точек локальных максимумов ту, в которой функция (11.19) принимает наи-
большее |
значение. Найденные таким образом |
значения |
||
x , x , , x |
определяют набор количества товаров |
x |
, кото- |
|
1 2 |
m |
|
i |
|
рые необходимо выпускать, чтобы при имеющейся функции затрат на их производство и спектре сложившихся цен обеспечить максимальную прибыль.
Пример 11.12. Пусть производиться два вида товаров, обозначим их количества через x и y. Пусть цены на эти това-
ры соответственно |
P 8 |
и |
P 10 |
, а |
функция затрат |
|
1 |
|
2 |
|
|
C x2 xy y2 . Найти максимум прибыли. |
Тогда, согласно |
||||
формуле (11.19),прибыль выражается функцией
x, y 8x 10y x2 xy y2 .
Условия локального экстремума приводят к системе ли-
2x y 8
нейных алгебраических уравнений
x 2 y 10,
решение которой определяет точку (2;4). Поскольку
a11 2 0, H2 a11a22 a122 3 0, то найденная точка определяет локальный максимум функции прибыли, который равен
max 28.
11.12.2. Задача ценовой дискриминации
Эта задача связана с распределением товара одного вида по разным рынкам с разными спросами с тем, чтобы максимизировать общую прибыль. Поскольку эластичность спроса на рынках неодинакова, на товар устанавливают разные цены, что ведет к так называемой ценовой дискриминации.
Сформулируем общую задачу. Пусть
чество одного и того же вида товара, продаваемого на m рынках по ценам Pi xi , т.е. цена на каждом рынке зависит от ко-
169

личества продаваемого товара. Допустим, что функция затрат зависит от общего количества продаваемого товара, т.е. C S x1 x2 xm . Тогда функция общей прибыли имеет
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
x P x |
x |
P x |
2 |
x |
|
P x |
m |
S x |
x |
2 |
x |
m |
. (11.22) |
1 1 1 |
|
2 2 |
|
m m |
1 |
|
|
|
|||||
Необходимое условие экстремума |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi 0, |
i 1,2, , m, |
|
|
|
|
|
|||
приводит к системе алгебраических уравнений для определе-
ния стационарных |
точек функции (11.22) |
в области |
|||||
x |
0, x |
2 |
0, , x |
m |
0 |
m - мерного евклидова пространства E m : |
|
1 |
|
|
|
|
|
||
Pi |
xi xi P xi S x1 x2 xm 0, i 1,2, , m. |
(11.23) |
|||||
|
Проанализируем доход Ri на каждом рынке в зависимо- |
||||||
сти от цены на товар |
xi . Так как Ri xi Pi , предельный доход |
||||||
выражается суммой первых двух слагаемых в левой части
(11.23)
Ri Pi xi Pi Pi 1 Pi xi  Pi Pi 1 1 Ei ,
Pi Pi 1 1 Ei ,
где Ei эластичность спроса на i - рынке. Так как Ei обычно
отрицательная величина, последнее равенство можно переписать в более удобной форме:
|
|
|
Ri Pi 1 1 |
|
Ei |
|
. |
(11.24) |
|
|
|
|
|
||||
|
1, то, |
Ri 0, т.е. |
|
|
|
|||
Если |
Ei |
|
рынок |
неэластичный. Если |
||||
S 0, то условие (11.24) требует выбора рынка с положительным предельным доходом, или эластичным способом, т.е. с
условием |
|
|
Ei |
|
1. Из уравнений (11.23) |
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
P |
1 1 |
|
E |
|
P |
1 1 |
|
E |
2 |
|
P 1 1 |
|
E |
m |
|
S , |
|||
|
|
|
|
|
|
||||||||||||||
1 |
|
|
1 |
|
2 |
|
|
|
|
m |
|
|
|
|
|||||
откуда и выводится условие «ценовой дискриминации»: чем меньше по абсолютной величине эластичность данного рынка при данном количестве продаваемого товара, тем выше должна быть цена на товар на этом рынке при условии максимизации прибыли.
170
Гессиан для функции прибыли в сокращенной форме записи имеет вид
|
|
|
|
|
|
|
|
|
i j, |
|
|
H m det |
|
|
|
P x |
|
2P |
S , |
|
|||
hij |
, |
hij |
|
i |
i |
i |
|
|
|
(11.25) |
|
|
|
|
|
|
|
|
S , |
|
i |
j, |
|
|
|
|
|
|
|
|
|
||||
i, j 1,2, , m.
Пример 11.13. Пусть имеется три рынка с количеством
продаваемого товара x1, x2 и |
x3 с ценами на этот товар соот- |
|
ветственно Pi ai bi xi , так |
что доход Ri xi |
ai bi xi . Пусть |
функция затрат имеет вид C A B x1 x2 x3 |
. Найти макси- |
|
мум прибыли.
В указанных соотношениях все постоянные величины положительны. Тогда функция прибыли выражается формулой
x1 a1 b1x1 x2 a2 b2 x2 x3 a3 b3 x3 A B x1 x2 x3 .
Условие локального экстремума приводит к системе уравнений ai 2bi xi B 0, i 1,2,3,
откуда находим единственную стационарную точку, опреде-
ляемую тремя равенствами: |
xi |
ai |
B |
, |
i 1,2,3. |
|||||
2bi |
||||||||||
|
|
|
|
|
|
|
|
|||
Гессиан функции прибыли, согласно (11.25), имеет вид |
||||||||||
|
2b1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H3 |
0 |
2b2 |
0 |
, откуда при bi |
0 получаем по крите- |
|||||
|
0 |
0 |
2b3 |
|
|
|
|
|
|
|
рию Сильвестра точку максимума, так как знаки главных миноров чередуются, начиная со знака «минус».
|
|
|
Для |
конкретизации |
возьмем |
|
числа |
a1 25,b1 5 ; |
||||||||||
a2 45,b2 4 ; |
a3 85,b3 10; |
A 10, B 5. |
Тогда получаем |
|||||||||||||||
распределение товара между рынками |
x1 2, x2 |
5, x3 4 при |
||||||||||||||||
ценах на них соответственно |
P 15, P 25, P 45. Нетрудно |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
подсчитать, |
|
что |
соответствующие |
|
эластичности |
|||||||||||||
|
E1 |
|
1,5, |
|
E2 |
|
1,25, |
|
E3 |
|
1,125 |
удовлетворяют |
принципу «цено- |
|||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
171 |
|
|
|
|

вой дискриминации»: чем меньше величина Ei i- го рынка,
тем выше должна быть цена товара на нем. Максимальная прибыль max 270.
11.12.3. Оптимальное распределение ресурсов
Рассмотрим типичную задачу оптимального распределения ресурсов на примере функции выпуска u a0 xy2 при допущении, что функция затрат на ресурсы x и y линейна, т.е.
имеет вид u P x P y, |
где |
P |
и |
P |
- |
соответствующие цены |
|||
|
1 |
2 |
|
|
1 |
|
2 |
|
|
на эти факторы. |
|
|
|
|
|
|
|
|
|
В точке |
x0 , y0 |
|
оптимального |
определения ресурсов |
|||||
линии уровня функций выпуска и затрат касаются. Эти линии
определяются |
|
соответственно |
|
|
уравнениями: |
|||||||
a |
0 |
xy2 C, P x P y A, или y b x 1 2 , y P |
|
P |
x A P , |
|||||||
|
|
|
|
1 |
2 |
|
1 |
2 |
|
2 |
||
где C>0 и A>0 – постоянные числа b C a0 . |
Условие касания |
|||||||||||
этих линий определяется уравнением b x 1 2 |
|
x0 |
P |
P . |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
Из |
|
|
этого |
уравнения |
находится |
значение |
||||
x |
0 |
b1 3 P |
2P 2 3 . Тогда из уравнения линии уровня функ- |
|||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
ции |
|
|
выпуска |
определяется |
|
|
значение |
|||||
y |
0 |
b x |
0 |
1 2 b1 3 2P |
P 1 3 . Отсюда получаем, что оптималь- |
|||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
||
ное распределение ресурсов x0 y0 |
должно быть произведено в |
|||||||||||
отношении |
P |
: 2P . |
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
11.12.4. Максимизация прибыли производства продукции
Функция прибыли обычно вычисляется по формуле |
||
K, L |
P F K, L WL RK, |
(11.26) |
где P цена продукции, |
F K, L производственная функция, |
|
W и R соответственно факторные цены на труд и капиталь-
172
ные затраты, L и K соответственно затраты трудовых ресурсов и капитала. Мы рассмотрим две задачи, связанные с определением максимума прибыли.
Оптимальный план. Точка K0 , L0 называется опти-
мальным планом, если в ней функция прибыли (11.26) принимает максимальное значение. Найти предельную норму замещения производственной функции F при оптимальном плане.
В точке локального экстремума первые производные функции прибыли K, L равно нулю, откуда имеем систему
двух уравнений: |
|
|
|
|
|
|
P F K |
0 |
, L R 0, |
P F |
K |
0 |
, L W 0. |
k |
0 |
L |
|
0 |
Как известно, предельная норма замещения вычисляется
по формуле F F , откуда при оптимальном плане по-
L K
лучаем W R.
R.
Максимизация функции прибыли. Найти оптимальный план и максимум функции прибыли (11.26), если
F K, L 2 KL 1 3.
3.
Таким образом, функция прибыли в данном случае имеет вид
K, L 2P K, L 13 WL RK.
Условия локального экстремума приводят к системе двух линейных алгебраических уравнений относительно координат К0 и L0 оптимального плана:
|
2 |
PL |
|
1 |
3 K |
|
2 |
3 |
R |
|
3 |
|
|
|
|
||||
0 |
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
2 |
|
|
13 L 2 3 |
|
||||
|
PK |
|
W . |
||||||
|
|
||||||||
|
3 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаем координаты оптимального плана:
K0=(2P/3)3/(R2W), L0=(2P/3)3/(RW2).
Подстановка этих величин в функцию прибыли дает ее максимум:
Пmax==(2P/3)3/(RW).
173
