2939

М.И. Зайцева В.Н. Макаров А.А. Сидоренко

ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ

Учебное пособие

Воронеж 2002

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

М.И. Зайцева В.Н. Макаров А.А. Сидоренко

ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ

Учебное пособие

Воронеж 2002

2

УДК 517.2

М.И. Зайцева М.И., Макаров В.Н., Сидоренко А.А. Элементы вычислительной математики: Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2002. 121 с.

Данное учебное пособие написано в соответствии с программой по курсу “Численные методы”, изучаемой сту-

дентами специальности 130100 “Самолето- и вертолетострое-

ние”. В пособии рассматриваются основные вычислительные методы, наиболее часто используемые в инженерных и научно-технических расчетах.

Предназначено для студентов второго курса дневного отделения.

Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97.0 и содержится в файле «ВычМат.rar»

Табл.13. Ил.21. Библиогр.: 9 назв.

Рецензенты: кафедра математики и физики ВВИРЭ; д-р. физ.-мат. наук Родин В.А.

Издается по решению редакционноиздательского совета Воронежского государственного технического университета.

©Зайцева М.И., Макаров В.Н., Сидоренко А.А., 2002

©Оформление. Воронежский государственный технический университет, 2002

3

1. ОСОБЕННОСТИ МАТЕМАТИЧЕСКИХ ВЫЧИСЛЕНИЙ РЕАЛИЗУЕМЫХ НА ЭВМ

1.1. ЭТАПЫ РЕШЕНИЯ ЗАДАЧИ НА ЭВМ

Наиболее эффективное применение вычислительной техники находит при проведении трудоемких расчетов в научных исследованиях. Тем не менее, при решении задач на ЭВМ основная роль все таки принадлежит человеку. Машина лишь выполняет его задания по разработанной программе.

Роль человека и машины легко уяснить, если процесс решения задачи разбить на отдельные этапы.

а) Постановка задачи. Этот этап заключается в содержательной (физической) постановке задачи и определения конечных целей решения.

б) Построения математической модели (Математическая формулировка задачи). Модель должна правильно (адекватно) описывать основные законы физического процесса. Построение или выбор математической модели из существующих требует глубокого понимания проблемы и знания существующих разделов математики.

в) Разработка численного метода. ЭВМ может выполнять лишь простейшие операции. Она не “понимает” постановки задачи даже в математической формулировке. Для ее решения должен быть найден численный метод, позволяющий свести задачу к некоторому вычислительному алгоритму. Разработкой численных методов занимаются специалисты в области вычислительной математики.

Специалисту-прикладнику для решения задачи, как правило необходимо из имеющегося набора методов выбрать наиболее пригодный в данном конкретном случае.

г) Разработка алгоритма построения блок-схемы. Процесс решения задачи записывается в виде последовательности элементарных арифметических и логических операций, приводящей к конечному результату. Эта последовательность называется алгоритмом решения задачи. Его можно изображать в виде блок - схемы.

д) Программирование. Алгоритм решения задачи записывается на понятном машине языке в виде точно определенной последовательности операций – программы для ЭВМ.

е) Отладка программы. Составленная программа содержит разного рода ошибки, неточности, описки. Отладка программы на

5

машине включает контроль программы, диагностику (поиск и определение содержания) ошибок и их исправление. Программа испытывается на решении контрольных (тестовых) задач для получения уверенности в достоверности результатов.

ж) Проверка расчетов. На этом этапе готовятся исходные данные для расчетов и проводится счет по отлаженной программе.

и) Анализ результатов. Результаты расчетов тщательно анализируются, оформляется научно-техническая документация.

В связи с повышением “интеллектуальных возможностей” ЭВМ и увеличением их числа, неуклонно возрастает доля машинных вычислений в общем объеме решения научно-технических задач. В связи с этим возрастает интерес к математическому моделированию и разработке численных методов.

1.2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ. ЧИСЛЕННЫЕ МЕТОДЫ

Основное требование, предъявляемое к математической модели, адекватность рассматриваемому явлению. Она должна достаточно точно (в рамках допустимой погрешности) отражать характерные черты явления. Вместе с тем, она должна обладать сравнительной простотой и доступностью исследования. При построении математических моделей получают некоторые математические соотношения (как правило, уравнения).

Пример. В начальный момент времени t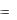

щееся на высоте h0 брошено вертикально вниз с начальной скоростью v0 . Найти закон движения тела, т.е. построить математиче-

скую модель, которая позволила бы математически описать данную задачу и определить параметры движения в любой момент времени.

Решение. Прежде всего надо принять некоторые допущения, если они не заданы. В частности, предположим, что данное тело имеет плотность >> плотности воздуха и сопротивление движению отсутствует. В этом случае закон движения имеет вид:

Эти формулы и являются искомой математической моделью свободного падения тела. Область применения ее весьма ограничена.

6

Во многих задачах о движении тела в атмосфере модель

(1.1) не может быть использована, т.к. ее применение давало бы неверный результат (движение капли, вход в атмосферу тела малой плотности, спуск на парашюте и др.).

Здесь требуется построение более точной математической модели, учитывающей сопротивлением воздуха. Если обозначить через F(t) силу сопротивления, действующую на тело массы m, то его движение можно описать с помощью уравнений

ской моделью для задачи движения тела в атмосфере. Суще-

ствуют и другие, более сложные модели подобных задач (о движении планера и т.п.).

Известно большое число математических моделей различных процессов или явлений. Вот некоторые из них, используемые в механике.

1.Модель абсолютно твердого тела позволила получить уравнения движения тел в динамике полета.

2.Модель идеального газа привела к системе уравнений Эйлера, описывающей невязкие потоки газов.

3.В гидродинамике широко известна модель на основе уравнений Навье-Стокса, в кинематической теории газов - уравнения Больцмана т.д.

4.В механике деформируего твердого тела известны математические модели, описывающие различные среды (упругую, упруговязкую и т.д.).

Имеются математические модели и для описания задач экономики, медицины, лингвистики и др. При использовании той или иной модели необходима правильная оценка области ее применимости. Для успешности решения задачи, которое зависит от выбора математической модели, нужны глубокие знания в той области, к которой принадлежит поставленная задача. Кроме того, необходимы знания соответствующих разделов математики и возможностей ЭВМ.

С помощью математического моделирования решение научнотехнической задачи сводится к решению математической задачи, являющейся ее моделью. Для решения математических задач ис-

7

пользуются следующие основные группы методов: графические,

осью абсцисс и будут искомыми корнями.

При использовании аналитических методов решение задачи удается выразить с помощью формул (простейшие алгебраические и трансцендентные уравнения, дифференциальные уравнения). На практике это слишком редкие случаи.

Основным инструментом для решения сложных математических задач в настоящее время являются численные методы. Они позволяют свести решение задачи к выполнению конечного числа арифметических действий над числами. Результаты при этом получаются в виде числовых значений. Многие численные методы разработаны давно. Однако при вычислениях вручную они могли использоваться лишь для решения не слишком трудоемких задач.

С появлением ЭВМ начался период бурного развития численных методов и их внедрение в практику, поскольку многие современные задачи требуют выполнения за сравнительно короткое время объема вычислений в миллионы, миллиарды и более операций.

Численный метод, наряду с возможностью поучения результата за приемлемое время, должны обладать и еще одним важным свойством - не вносить в вычислительный процесс значительных погрешностей.

1.3. ТОЧНОСТЬ ВЫЧИСЛЕНИЙ

ограниченности ее разрядной сетки, может оперировать лишь с некоторым конечным подмножеством этого множества. Так, во многих моделях ЭВМ диапазон представляемых целых чисел даже в режи-

8

ме с удвоенной точностью находится примерно в интервале от

2 109 до 2 109 .

При решении научно-технических задач в основном используются действительные числа. Для их представления почти во всех машинах используется форма с плавающей точкой. Десятичное чис-

d1 0 получаем нормализованную форму числа с плавающей точ-

кой.

Все сказанное распространяется и на числа, записанные в других системах счисления. Число N в системе счисления с основанием можно представить в виде:

То есть, в ЭВМ невозможно сколько-нибудь детально отобразить континуум действительных чисел. Более того, действительные числа с модулем большим максимального элемента не могут быть отображены вообще. По роду примы то же самое верно в отношении ненулевых действительных чисел, меньших по абсолютной величине по сравнению с наименьшим положительным числом из

M .

Пример. В случае десятичных чисел при четырехразрядном представлении все значения, находящиеся в интервале между чис-

9

последнего разряда. Числа, меньше этой разности, воспринимаются как машинный нуль. То есть, ЭВМ оперирует с приближенными значениями действительных чисел. Мерой точности приближенных чисел является погрешность.

Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычислений или измерения:

x x a .

Относительная погрешность - это отношение абсолютной погрешности к приближенному значению числа

Так как истинное значение величины x обычно неизвестно, то приведенные выражения для погрешностей практически не могут

грешности приближенного числа a . В этом случае истинное значение x находится в интервале 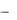a a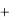, a a .

Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например, значение a 0.734 могло

10