2939

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

x y2 3lg x

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

По формуле (4.14) вычисляем k0

		k0	1	8.64	0.434		0.0390,
				4.91	0.1956
			97.91
			97.91
отсюда по формуле (4.16)				находим		y1 1.7 0.0390		1.6610.
Повторяя этот процесс с полученными значениями корней,								получим
x2	1.2343,	y2 1.6615 и т.д.
4.8.	МЕТОД ИТЕРАЦИИ ДЛЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ
	Пусть даны два уравнения с двумя неизвестными
				F1 (x, y)		0		(4.10)
				F2 (x, y) 0,				(4.10)
				F2 (x, y) 0,
где	F1 (x, y) ,	F2 (x, y) непрерывные функции. Требуется найти

действительные корни этой системы.

Предположим, что эта система имеет только изолированные

корни. Начальное	приближение	( x0 , y0 )	можно найти графически,
построив кривые	F1 (x, y) 0 ,	F2 (x, y)	0 и определив коорди-
наты их точек пересечения.
Представим систему (4.10) в виде:

		x	1(x, y)		(4.17)
		y	2 (x, y)		(4.17)
		y	2 (x, y)
и построим	последовательные приближения по следующим форму-
лам:
	x1	1 (x0 , y0 ) ;	y1	2 (x0 , y0 ) ;
	x2	1(x1, y1) ;	y2	2 (x1, y1) ;	(4.18)
……………………………………….
xn 1		1 (xn , yn ) ;	yn 1	2 (xn , yn ) .
Если	существуют пределы			lim xn ,	lim yn , то
				n	n
точка ( ,	) является решением системы (4.10).

Достаточные условия сходимости итерационного процесса

содержатся в следующей теореме.
Теорема.	Пусть	в	некоторой	области
R a x A, b	y B имеется одно решение системы (4.17).

Если выполнены условия:

1)функции 1(x, y) и 2 (x, y) определены и непрерывно дифференцируемы в R ;

2)начальное приближение ( x0 , y0 ) и все последующие при-

	ближения ( xn , yn ) принадлежат R ;
4)	3) в R выполнены неравенства
		1(x, y)	2	(x, y)	q1	1
		1(x, y)	2	(x, y)
		x		x
		x		x
		1(x, y)		(x, y)	q2	1,
		1(x, y)	2	(x, y)
		y		y
		y		y

то процесс последовательных приближений (4.18) сходится к кор-

ням системы (4.17), т.е. существуют пределы lim xn , n

lim yn .
n
Пример.	Решить методом итераций систему уравнений
		x	3lg x		y 2	0
		2x2		xy 5x 1 0.
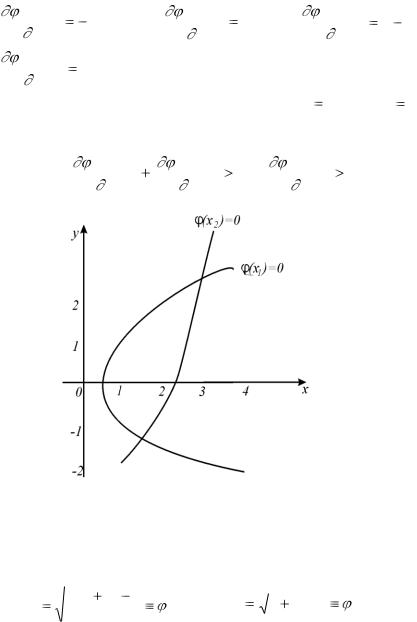
Решение.	Построим			кривые		1(x, y)		x	3lg x y2 и
2 (x, y) 2x2	xy	5x	1	и	определим		графически точки их
пересечения (рис. 13).		Это будут точки (14.;					14.)	и	(3.4; 2.2) .

Для применения метода итерации необходимо привести систему к виду (4.11), что можно сделать различными путями. Если приведем систему к виду:

то производные

1(x, y)	3lg e	;	1	(x, y)	2 y ;	2	(x, y)	2	1	;
x	x			y			x		x

(x, y)

Отсюда видно,

что в окрестности точки

x0 3.4 ,

y0 2.2

будут иметь место неравенства

(x, y)

1(x, y)

(x, y)

4 .

Рис. 13

Это показывает, что при таком виде системы итерационный процесс расходится. Определим теперь x из второго уравнения, а y из первого и запишем нашу систему в таком виде:

	x( y	5) 1
x	x( y	5) 1	1	(x, y);	y	x 3lg x	2 (x, y).

		2
		2

Здесь

1(x, y)

5 y

;

1(x, y)

;

2 2 x(5 y) 1

3lg e

2 (x, y)

;

3lg x

За

область

изоляции

корня

можно

принять

прямоугольник

x 4 ,

2.5.

Легко установить,

что в этом прямо-

угольнике

1(x, y)

0.60 ,

1(x, y)

0.32 ,

2 (x, y)

0.34.

Отсюда

1(x, y)

2 (x, y)

0.60

0.34

0.94

1(x, y)

2 (x, y)

0.32

0.32 1.

Следовательно, итерационный процесс сходится, но так как

сумма производных

по

сравнительно

велика,

то скорость схо-

димости оказывается небольшой.

Вычисления

нулевыми

приближениями

x0 3.4 ,

2.2 будем производить по формулам

xn ( yn 5) 1

yn 1

3lg xn

( n

0,1,2,...).

При различных значениях

n эти вычисления дают следующие ре-

зультаты

3.4(2.2

3.426 ,

3.426

3lg3.426

2.243,

3.451,

2.205,

3.466,

2.255 ,

3.475,

2.258,

3.480 ,

2.259 ,

f (x)

x6 3.483,	y6 2.260.
Таким образом,	можно принять	3.483 ,	2.262 .

5.ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ

5.1.ПОСТАНОВКА ВОПРОСА

Обычное нахождение производной с помощью таблицы производной при численном решении задач применимо не всегда, в частности, если функция задана таблично, а также при решении

дифференциальных уравнений разностными методами. В этих случаях обычно прибегают к приближенному дифференцированию.

Для вывода формул приближенного дифференцирования за-

меняют данную функцию			f (x)	на отрезке	a, b	интерполирую-
щей функцией P(x) (чаще всего полиномом), а затем полагают:
	f (x)		P (x) .			(5.1)
Аналогично поступают при нахождении производных высших
порядков функции f (x) .
Если для	интерполирующей функции				P(x) известна по-
грешность R(x)	f (x)	P(x) , то погрешность производной P (x)
выражается формулой
	r(x)	f (x)		P (x) R (x) ,		(5.2)

то есть погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же самое справедливо и для производных высших порядков.

Следует отметить, что приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Действительно, близость друг к другу ординат двух кривых

y 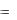f (x) и Y P(x)

на отрезке a, b еще не гарантирует близости на этом отрезке их производных f (x) и P (x) , т.е. малого расхождения угловых ко-

эффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента (рис. 14).

Рис.14

5.2. ФОРМУЛЫ ПРИБЛИЖЕННОГО ДИФФЕРЕНЦИРОВАНИЯ, ОСНОВАННЫЕ НА ПЕРВОЙ ИНТЕРПОЛЯЦИОННОЙ

ФОРМУЛЕ НЬЮТОНА

Пусть имеем функцию		f (x) , заданную в равноотстоящих
точках xi	(i 0,1,2, . . n. ,)	отрезка	a, b с помощью значений
yi f (xi ) .	Для нахождения	на a, b	производных y f (x) ,

y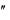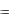f (x) и т.д. функцию f (x) приближенно заменим интерполяционным полиномом Ньютона, построенного для системы узлов

x0 , x1,..., xn , т.е.			f (x)	Pn (x).
Имеем
	y(x)	y0	q y0		q(q 1)		2	y0	q(q 1)(q 2) 3	y0
	y(x)	y0	q y0			2!		y0	3!	y0
						2!			3!
	q(q	1)(q	2)(q	3)		4 y0	...,

		4!
		4!

где q	x	x0	,	h x	x	1	(i 1,2,..., n) .
где q			,	h x	x		(i 1,2,..., n) .
		h		i	i
		h
						86

Перепишем ее, выполнив умножение:

y(x)

q y0

3q2

2q 3

6q3

11q2

4 y0 ....

Так как

то

y (x)

2q 1

3q 2

6q 2 3

2q3

9q 2

(5.3)

11q

3 4

y0 ....

Аналогично, так как

y (x)

d ( y )

d ( y ) dq

то

y (x)

6q 2

18q

.... . (5.4)

Таким же способом в случае надобности можно вычислить и

производные функции y(x) любого порядка.

Иногда требуется находить производные функции

y в основ-

ных табличных точках xi . В этом случае формулы численного

дифференцирования упрощаются. Так как каждое табличное											значе-
ние можно считать за начальное, то положим								x x0 , q			0; то-
гда будем иметь:
Pn (x0 )	1	y0	2 y0		3 y0		4 y0		5 y0	.....	(5.5)
Pn (x0 )	h	y0	2	3		4		5		.....	(5.5)
	h		2	3		4		5

P (x	0	)	1	2	y	0	3	y	0	11	4	y	0	5	5	y	0	..... .	(5.6)

n			h2							12				6

Пример. Найти							y (50)			функции y					lg x ,			заданной табли-

цей 9.

				Таблица 9
x	y	y	2 y		3 y
50	1.6990	414	-36		5
55	1.7404	378	-31
60	1.7782	347
65	1.8129

Решение. Здесь h 5 . Используя первую строчку таблицы, на основании формулы (5.5), с точностью до разностей третьего порядка, будем иметь

		y (50)			1	(0.0414	0.0018	0.0002)	0.0087.
		y (50)		5		(0.0414	0.0018	0.0002)	0.0087.
				5
	Для оценки точности найденного значения, заметим, что так
как	табулированная					выше	функция	есть	y	lg x , то
yx	M	0.43429	.	Следовательно,				y (50)	M	0.0087.
yx			.	Следовательно,				y (50)		0.0087.
	x	x							50

Таким образом, результаты совпадают с точностью до четвертого десятичного знака.

5.3. КОНЕЧНО-РАЗНОСТНЫЕ АППРОКСИМАЦИИ ПРОИЗВОДНЫХ

Пусть отрезок				a, b		разбит на n ( n			2 ) равных частей точ-
ками	xi : a		x0	x1	x2	...	xi 1	xi	xi	1 ... xn	b .
Разность между соседними значениями										аргумента	постоян-
на, т.е. шаг		h	xi	xi 1 ,		( i	1,2,..., n ). Далее, пусть на				отрезке
a, b	определена функция					y	f (x) ,	значения которой в точках xi
равны	yi	f (xi ) ,		( i	0,1,2,..., n ).

Запишем выражения для первой производной функции в точке xi с помощью отношения конечных разностей:

а) аппроксимация с помощью разностей вперед (правых разностей)

y (xi )

xi 1

h ,

yi 1

yi ,

y (xi )

( i

0,1,2,..., n

1);

(5.7)

б) аппроксимация с помощью разностей назад (левых разно-

стей)

y (xi )

xi 1

h ,

yi 1 yi ,

y (xi )

yi 1

( i

1,2,..., n ) ;

(5.8)

в) аппроксимация с помощью центральных разностей (точка

xi является центром системы точек

1, xi , xi

1 )

y (xi )

xi 1

2h ,

yi 1

yi ,

y (xi )

yi 1

( i

1,2,..., n

1).

(5.9)

Аппроксимация производной с помощью центральных разностей представляет собой среднее арифметическое соотношений (5.7)

и (5.8) в точках xi , ( i	1,2,..., n	1).
Отметим, что соотношения (5.7) и (5.9) не позволяют вычис-
лить производную в точке	xn b ,	а	(5.8) и (5.9) - в точке
x0 a .
Можно показать, что для функции y			f (x) , имеющей непре-

рывную производную до второго порядка включительно, погрешность аппроксимации производных разностями вперед и назад имеет один и тот же порядок o(h) , а погрешность аппроксимации цен-

тральными разностями (5.9) для функции y f (x) , имеющей не-

f (x)

не может быть найдена с помощью элементарных средств или является слишком сложной. Кроме того, на практике функция часто задается таблично и тогда само понятие первообразной теряет

F(x)

F (a) . Однако во многих случаях первообразная

прерывную производную до третьего порядка включительно, имеет порядок o(h2 ) .

Приближенное значение производной второго порядка в точке xi выразим через значения функции yi 1 , yi , yi 1 . Для этого представим вторую производную с помощью правой разности:

y (xi )

xi 1

h ,

yi 1

yi ,

а производные первого порядка

yi и

1 - с помощью

левых

разностей:

yi 1

y (xi 1 )

yi 1

y (xi )

yi yi

и окончательно получим

y (xi )

yi 1

2 yi

1,2,..., n

(5.10)

Погрешность последней аппроксимации имеет порядок o(h 2 )

для функции

f (x) ,

имеющей непрерывную производную до

четвертого порядка включительно на отрезке a, b . Естественно,

что представление (5.10) с помощью конечных разностей позволяет вычислять значения второй производной только во внутренних точках отрезка.

	6.	ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Если	функция f (x) непрерывна на отрезке a, b и известна
ее первообразная		F(x) , то определенный интеграл	от этой функ-
ции может	быть	вычислен по формуле Ньютона	– Лейбница

f (x)dx F (b)

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.62 Mб02926.pdf
#
15.11.20222.63 Mб02931.pdf
#
15.11.20222.64 Mб02934.pdf
#
15.11.20222.64 Mб12937.pdf
#
15.11.20222.64 Mб22938.pdf
#
15.11.20222.65 Mб12939.pdf
#
15.11.20222.65 Mб12940.pdf
#
15.11.20222.65 Mб32942.pdf
#
15.11.20222.66 Mб02943.pdf
#
15.11.20222.66 Mб12945.pdf
#
15.11.20222.67 Mб12947.pdf