Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2939

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

итоге получаем систему уравнений, для которой метод итерации сходится

10x1	2x2	x3	2x4	4
x1	5x2	x3		1
x1	2x2	5x3	x4	2
3x1			9x4	10.

3.3.МЕТОД ЗЕЙДЕЛЯ

Метод Зейделя представляет собой модификацию метода итераций. Основная его идея заключается в том, что при вычисле-

нии	(k 1) -го приближения неизвестной xi						учитываются уже вы-
численные		ранее		(k 1) -е		приближения неизвестных
x1,	x2 , ...,	xi	1 .
	Запишем систему (3.6) в виде:
				n
			x1		1 j x j	1
				j	1
				n
			x2		2 j x j	2
				j	1
			................................
					n
			xn		nj x j	n .
				j	1
	Выберем		произвольно начальные				приближения корней

x1(0) , x2(0) ,..., xn(0) . Тогда первое приближение по методу Зейделя вычисляется по формулам:

			n
		x1(1)	1 j x (0)j	1
		j	1
			n
		x2(1)	21x1(1)	2 j x j	2
			j	2
		.......... .......... .......... ..
		n 1
		xn(1)	nj x (1)j	xnn(0)	n
		j	1
Так	же	вычисляются		следующие		приближения

X (2) , X (3) ,... .

Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации. Процесс Зейделя может сходиться даже в том случае, если расходиться процесс итерации. Однако, возможны случаи, когда процесс Зейделя сходится медленнее процесса итерации или, когда процесс итерации сходится, а процесс Зейделя расходится.

Пример. Методом Зейделя решить систему уравнений

10x1 x2 x3 12

2x1 10x2 x3 13 2x1 2x2 10x3 14.

Решение. Приведем эту систему к виду, удобному для итера-

ции,

x1	1.2 0.1x2	0.1x3
x2	1.3 0.2x1	0.1x3
x3	1.4 0.2x1	0.2x2 .

В качестве нулевых приближений корней возьмем x1(0) 1.2, x2(0) 0, x3(0) 0.

Применяя процесс Зейделя, последовательно получим:

x	(1)	1.2	0.1	0	0.1	0		1.2
1
x2(1)		1.3	0.2	1.2	0.1		0	1.06
x3(1)		1.4	0.2	1.2	0.2		1.06		0.948.

	x	(2)	1.2	0.1 1.06			0.1		0.948				0.9992
1
	x2(2)		1.3	0.2	0.9992			0.948				1.00536
	x3(2)		1.4	0.2	0.9992			0.2		1.005366				0.999098.
Результаты вычислений с точностью												до четырех знаков по-
мещены в таблицу 7.
											Таблица 7
	k			(k )			(k )					(k )
			x1				x2					x3
	0		1.2000			0.0000						0.0000
	1		1.2000			1.0600						0.9480
	2		0.9992			1.0054						0.9991
	3		0.9996			1.0001						1.0001
	4		1.0000			1.0000						1.0000
	5		1.0000			1.0000						1.0000
Точные значения корней:						x1	1,		x2			1,	x3	1.

4. МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4.1. ОТДЕЛЕНИЕ КОРНЕЙ

При решении многих алгебраических и трансцендентных уравнений точное значение их корней определить бывает достаточно сложно. Поэтому важное значение приобретают способы приближенного нахождения корней и оценки степени их точности.

Пусть дано уравнение

f (x) 0 ,

(4.1)

где f (x) - непрерывная функция от x . Всякое значение , обращающее функцию f (x) в нуль, т.е. такое, что f ( ) 0 , называется корнем уравнения (4.1) или нулем функции f (x) .

Приближенное нахождение действительных корней уравнения обычно складывается из двух этапов:

1)отделение корней, т.е. установление промежутков, в которых содержится только один корень уравнения;

2)уточнение приближенных корней, т.е. доведение их до заданной степени точности.

Известно, что если функция f (x) непрерывна и принимает

на концах	отрезка a, b значения	разных знаков, т.е.
f (a) f (b)	0 , то внутри этого промежутка	имеется хотя бы один

корень уравнения. Отделение корней уравнения f (x) 0 для непрерывной в области определения функции f (x) можно осуществить различными способами.

1)Составляют таблицу значений функции y 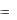f (x) на

определенном промежутке изменения аргумента x , и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень находится между ними.


2)	Уравнение	f (x) 0	заменяют		равносильным
(x)	(x) . Строят графики функций y			(x) и	y	(x) ; ис-

комый корень является абсциссой точки пересечения этих графиков.

3)Строят график функции y 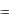f (x) на промежутке изме-

нения x ; тогда абсцисса			точки пересечения графика с осью OX -
корень уравнения, т.е. f (			)	0 .
Пример. Выяснить,				сколько корней	имеет	уравнение
4 e x 2x2	0 ,	и найти промежутки, в которых находятся эти
корни.
Решение. Рассмотрим три функции:
f (x) 4 - ex		2x2 ;		(x) 4 2x2 ;	(x) ex .
Уравнение	f (x)	0 эквивалентно уравнению			(x)	(x) . Оте-

лим его корни двумя способами (таблица 8).

			Таблица 8
x	f (x)	(x)	(x)

-3.0	-14.05	-14.00	0.05
-2.0	-4.14	-4.00	0.14
-1.0	1.63	2.00	0.37
0.0	3.00	4.00	1.00
1.0	-0.72	2.00	2.72


1.	Из таблицы значений					функции	f (x) на промежутке
3.0; 1.0		с шагом изменения x , равным 1, видно, что существуют
корни на отрезках			2;	1	и 0; 1 , так как		имеют разные знаки.
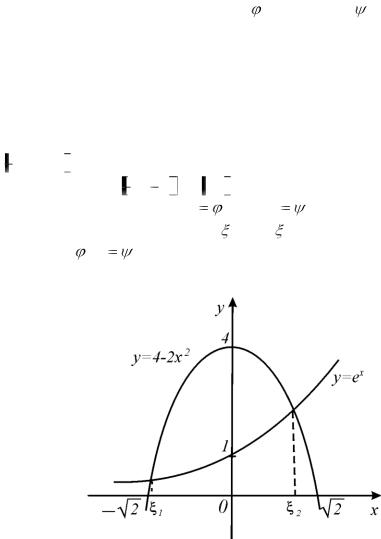
1.	Графики функций				y	(x) и y	(x) пересекаются в
двух точках, абсциссы				которых		1 и	2 являются решениями
уравнения		(x)	(x) , заключенными в указанных промежутках

(рис. 5).

Рис.5

После отделения корней производится итерационное уточнения каждого корня одним из существующих методов.

Рассмотрим простейшие методы уточнения корней.

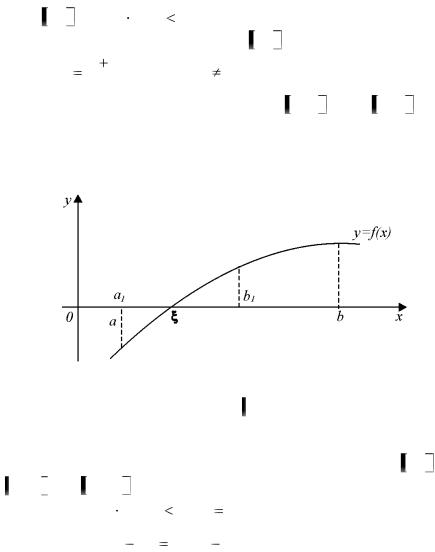
4.2. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ

Пусть дано уравнение (4.1), причем функция f (x) непрерыв-

на на a, b и	f (a) f (b)		0 (рис. 6).	Для вычисления корня урав-
нения (4.1), принадлежащего отрезку				a, b , найдем середину этого
отрезка x0	a b	. Если	f (x0 ) 0 , то для продолжения вычисле-
	2

ний выберем ту из частей данного отрезка a, x0 или x0 , b , на концах которой функция f (x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1 (рис. 6).

Рис.6

Новый суженный промежуток a1,b1снова делим пополам и проводим вычисления по разобранной схеме и т. д. В результате

получаем на каком-то этапе				или точный корень уравнения (4.1),
или же бесконечную последовательность вложенных отрезков						a, b ,
a1,b1 , …, an , bn	, таких, что
f (an )	f (bn )		0	( n	1, 2, ... ),	(4.2)
b	a		1	(b	a) .	(4.3)
		n
n			2n

Число – общий предел последовательностей

bn –

является корнем уравнения

f (x)

0 .

Оценку погрешности на n -ом шаге вычислений можно полу-

чить из соотношения (4.3)

в виде

0 b

(4.4)

Здесь an

с точностью

, не превышающей

a) .

Метод деления пополам сходится для любых непрерывных

функций, устойчив к ошибкам

округления и легко реализуется на

ПЭВМ.

Пример. Методом половинного деления с точностью

10 2

найти корень уравнения 4

e x

2x2

0 (

0 ).

Решение. В предыдущем примере при отделении корней урав-

нения было установлено, что искомый корень

принадлежит от-

резку 0; 1 . На каждом шаге вычислений значение корня принимаем

равным

с погрешностью

. Будем произ-

водить вычисления и выбирать последовательность

вложенных от-

резков

an , bn ,

используя условие

f (an )

f (bn ) 0 . Имеем

a,b

0;1 ,

a b

0.5.

Так

как

f (a)	3,	f (x1)		1.8513			и
a1	x1	0.5,	b1	b	1;		d1
a1, b1		0.5;1 ,		x2		a1	b1
a1, b1		0.5;1 ,		x2			2
							2
	Здесь		f (a1)		1.8513,
следовательно,			a2	x2 0.75,
Тогда

f (a) f (x1) 0 , то полагаем b1 a1 0.5. Тогда

0.5	1	0.75.

2
2
f (x2 )	0.758,		f (a1) f (x2 ) 0 ,
b2 b1		1; d2	b2 a2 0.25.

a2 , b2	0.75;1 , x3	a2	b2	0.875; d3	b3 a3	0.125.
			2

B(b, f (b)) :

Производя вычисления далее,	можно убедиться, что заданная
точность достигается на 7-ом шаге:	x7 0.8828125 с погрешно-

стью d7 0.00781250	0.01.
4.3.	МЕТОД ХОРД

Пусть дано уравнение (4.1), где f (x) – непрерывная дважды дифференцируемая функция на отрезке a, b . Пусть для опре-

деленности f (x) 0 при	a	x	b . Тогда кривая будет выпукла
вниз. Возможны два случая:	1)	f (a)	0 (рис.7)

Рис. 7

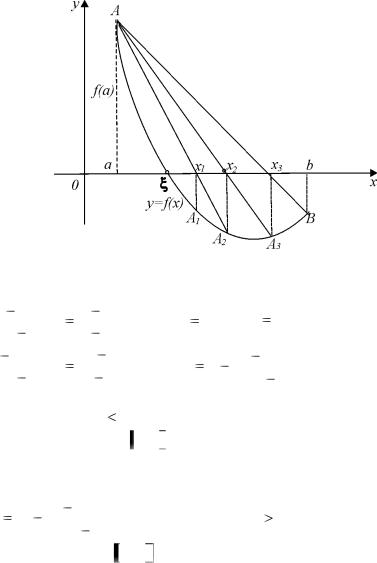
2) f (a) 0 (рис. 8).

Проведем хорду AB , соединяющую концы кривой y f (x) . За приближенное значение искомого корня примем абсциссу x1 точки пересечения этой хорды с осью OX . Для разыскания этого приближенного значения напишем уравнение прямой AB , проходящей через две заданные точки A(a, f (a)) и

Рис. 8

f (a)

. Так как

0 при

x , то,

следовательно,

f (b)

f (a)

, откуда

(b a) f (a)

f (b)

f (a)

b a

f (b) f (a)

Чтобы получить более точные значения корня, определяем

f (x1 ) . Если

f (x1)

0 , тогда за новый

промежуток изоляции кор-

ня можно принять

x1,b .

Соединив

точки

A1 (x1, f (x1)) и

B(b, f (b)) ,

получим в точке пересечения

хорды

с осью

второе

приближение

x2 ,

которое

вычислим

по формуле

x1 ) f (x1 )

Если же f (x )

0 ,

то

применим

эту

f (b) f (x1 )

формулу к отрезку

a, x1

. Повторяя этот прием несколько раз,

бу-

дем получать все более точные значения корня x3 , x4 ,... и т.д.

В первом случае конец b отрезка изоляции неподвижен и последовательные приближения корня находятся по формуле

xn 1	xn	(b	xn ) f (xn )	.	(4.5)
xn 1	xn	f (b) f (xn )		.	(4.5)
		f (b) f (xn )
Во втором случае	неподвижен конец a , а последовательные
приближения имеют вид:

				xn 1					xn				(xn		a) f (xn )			.						(4.6)
				xn 1					xn				f (xn )			f (a)		.						(4.6)
													f (xn )			f (a)
	Если		x		- точный корень уравнения (4.1), изолированный на
отрезке a, b , а								- приближенное значение корня, найденное ме-
тодом хорд, то оценка погрешности																этого приближенного значения
такова:
				x							f (a)				f (b)	max			f	(x)		.		(4.7)


														2						(x) 3
														2		a,b			f	(x) 3
	Пример. Методом хорд найти положительный корень уравне-
ния x3		0.2x 2				0.2x				1.2				0 с точностью						до	0.002 .
	Решение.					Найдем						интервал				изоляции					корня.		Так	как
f (1)		0.6	0		и			f (2)				5.6			0 , то искомый корень								лежит в
интервале (1,2).					Для				того				чтобы уменьшить количество вычисле-
ний,	разделим этот интервал пополам. Так как																				f (1.5)		1.425	0 ,
1	1.5 . Последовательно применяя формулу (4.5), будем иметь
	x1	1	(1.5				1)			0.6				1	0.15		1.15;

			1.425						0.6
			1.425						0.6
	f (x1)				0.173;
	x2	1.15			(1.5					1.15)				0.173		1.15				0.040 1.190;

							1.425					0.073
							1.425					0.073
	f (x2 )				0.036;
	x3	1.190					(1.5			1.190)					0.036		1.190				0.008		1.198;

							1.425							0.036
							1.425							0.036
	f (x3 )				0.0072;

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.62 Mб02926.pdf
#
15.11.20222.63 Mб02931.pdf
#
15.11.20222.64 Mб02934.pdf
#
15.11.20222.64 Mб12937.pdf
#
15.11.20222.64 Mб22938.pdf
#
15.11.20222.65 Mб12939.pdf
#
15.11.20222.65 Mб12940.pdf
#
15.11.20222.65 Mб32942.pdf
#
15.11.20222.66 Mб02943.pdf
#
15.11.20222.66 Mб12945.pdf
#
15.11.20222.67 Mб12947.pdf