
2939
.pdf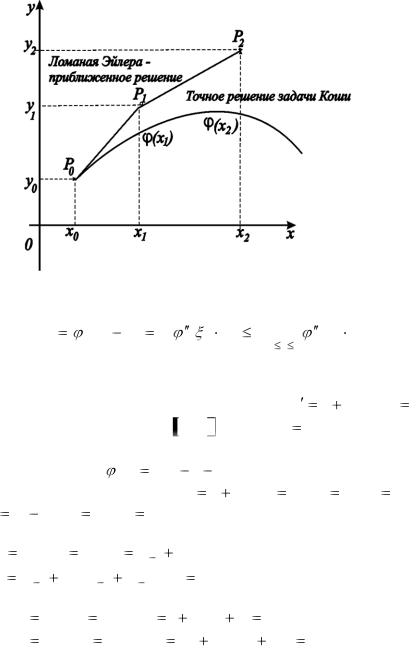
|
|
|
|
|
|
|
|
|
|
Рис.18 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Погрешность метода на одном шаге имеет порядок h2 , так как |
||||||||||||||||||||||||
|
|
d |
0 |
|
(x ) |
y |
|
1 |
|
|
( ) |
|
h2 |
1 |
max |
|
|
(x) |
|
h2 . |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
2 a x |
b |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ym |
|
|||||
|
После m шагов погрешность вычисления значения |
в ко- |
|||||||||||||||||||||||
нечной точке отрезка возрастает не более чем в m раз. |
|
|
|
||||||||||||||||||||||
|
Пример. Найти решение |
задачи Коши |
y |
x |
y , |
y(0) 1 |
|||||||||||||||||||
методом Эйлера на отрезке |
|
0;0.4 , с шагом h |
|
|
|
0.1 . Сравнить по- |
|||||||||||||||||||
лученные результаты с точным значением. Аналитическое |
решение |
||||||||||||||||||||||||
задачи имеет вид |
(x) |
|
2e x |
x |
1. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Решение. |
Здесь |
|
f (x, y) x y; |
m |
4; |
a |
0; |
b |
0.4; |
|||||||||||||||
h |
(b |
a) / m |
0.4 / 4 |
0.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Используя рекуррентные формулы: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x0 |
0; |
|
y0 |
1; |
xi |
xi 1 |
0.1; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
yi |
yi |
1 0.1(xi 1 |
yi |
1 ) |
|
|
(i 1, 2,3, 4), |
|
|
|
|
|
|
|
|
|
|
||||||||
последовательно |
находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
при i 1: x1 |
0.1; |
|
y1 |
1 |
0.1(0 1) |
1.1; |
|
|
|
|
|
|
|
|
|||||||||||
при |
i |
2 : |
|
x2 |
0.2; |
|
y2 |
1.1 |
0.1(0.1 |
1.1) |
|
|
1.22; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
|
|
|
|
|
|
|
|
|
|
||

при |
i |
3 : |
x3 |
0.3; |
|
y3 |
1.22 |
0.1(0.2 |
1.22) |
1.362; |
|||
при |
i |
4 : |
x1 |
0.4; |
|
y4 |
1.362 |
0.1(0.3 |
1.362) 1.5282. |
||||
|
Обозначим di |
|
yi |
(xi ) |
|
(i 1,2,3,4) |
и представим ре- |
||||||
зультаты вычислений в таблице 11. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 11 |
||
|
i |
|
xi |
|
|
|
yi |
|
|
(xi ) |
di |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
0.1 |
|
|
1.1 |
1.110342 |
0.005342 |
|
||||
|
2 |
|
0.2 |
|
|
1.22 |
1.242805 |
0.011793 |
|
||||
|
3 |
|
0.3 |
|
1.362 |
1.399718 |
0.019572 |
|
|||||
|
4 |
|
0.4 |
|
1.5282 |
1.583649 |
0.028738 |
|
|||||
|
|
|
|
|
|
МЕТОДЫ РУНГЕ-КУТТА |
|
|
|||||
|
Численные методы решения задачи Коши |
|
|
|
|||||||||
|
|
|
|
|
|
y |
f (x, y) , |
y(x0 ) |
y0 |
|
|
||
на |
равномерной сетке |
x0 |
a, x1, x2 ,..., xm |
b |
отрезка |
a,b с |
|||||||
шагом |
h |
|
b a |
|
являются методами Рунге-Кутта, если, начиная с |
||||||||
|
m |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
данных ( x0 , y0 ) , |
решение ведется по следующим рекуррентным |
||||||||||||
формулам: |
|
|
|
|
|
|
|
|
|
|
|
||
xi |
xi |
1 |
|
h , |
yi yi |
1 |
yi 1 |
( i |
1,2,..., m ), |
|
|
||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
yi |
1 |
|
|
d j k ji 1 , |
|
|
|
|
|
|
(7.5) |
||
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
k ji 1 |
hf (xi 1 |
c j h, yi 1 |
c j k ji |
11 ) . |
|
|
|
|
|||||
|
Метод называют методом Рунге-Кутта порядка p, |
если он |
|||||||||||
имеет |
p-й |
порядок точности по шагу h, |
на сетке. |
Порядок точно- |
|||||||||
сти |
p, |
достигается с помощью формул (7.5) при определенных зна- |
|||||||||||
чениях коэффициентов ci |
и |
di ( i |
1,2,..., p ); |
c1 |
всегда полагают |
||||||||
равным нулю. Эти коэффициенты вычисляют по следующей схеме:
102

1) |
точное |
решение |
(x0 h) |
и его |
приближение |
y1 y0 |
y0 (h) |
представляют |
в виде |
разложения |
по формуле |
Тейлора с центром x0 вплоть до слагаемого порядка h p 1;
2)из равенств подобных членов при одинаковых степенях h
вдвух разложениях получают уравнения, решая которые находят
коэффициенты ci и di .
Эти методы позволяют строить схемы различного порядка точности. Заметим, что метод Эйлера можно назвать методом Рунге-
Кутта первого порядка. Действительно, для p 1, c1 0, d1 1 формулы (7.5) преобразуются в соотношения (7.4)
xi |
|
xi 1 |
h, |
|
|
yi |
yi |
1 |
yi 1, |
|
|
(i 1,2,..., m), |
|||||
y |
i |
1 |
d k i 1 |
k i 1 |
, |
k |
i 1 |
hf (x |
i 1 |
, y |
i 1 |
), |
|
|
|||
|
|
1 1 |
1 |
|
1 |
|
|
|
|
|
|
||||||
или |
|
xi |
xi 1 |
h, |
|
yi |
yi |
1 |
hf (xi |
1, yi 1). |
|||||||
|
|
Метод Рунге-Кутта второго порядка называют методом Эйле- |
|||||||||||||||
ра–Коши, если p |
2, c |
0, |
c |
|
1, |
d |
d |
|
|
1 |
. |
||||||
2 |
2 |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Алгоритм метода Эйлера-Коши получается из формул (7.6):
xi |
|
xi 1 |
h, |
|
|
|
|
|
|
|
|
|
yi |
yi 1 |
|
|
|
yi 1, |
|
|
|||||||||||
|
y |
|
|
|
1 |
k i |
1 |
k i 1 |
, |
|
|
k i |
1 |
|
hf (x |
|
|
, y |
|
|
|
), |
(7.6) |
||||||||
|
i |
1 |
|
|
|
|
|
|
|
|
i |
1 |
i |
1 |
|||||||||||||||||
|
|
|
2 |
1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k2i |
|
1 |
|
hf (xi 1 |
h, yi 1 |
|
|
hf (xi 1, yi |
1 )) |
|
|
|
(i |
|
|
1,..., m). |
|||||||||||||||
|
|
|
Пример. Решить задачу Коши |
|
y x |
|
y , y(0) 1 методом |
||||||||||||||||||||||||
Эйлера-Коши на отрезке |
|
0;0.4 , с шагом h |
|
|
0.1 . |
|
|||||||||||||||||||||||||
|
|
|
Решение. Формулы |
|
(7.6) |
|
в данном случае примут вид |
||||||||||||||||||||||||
k i 1 |
|
|
h(x |
i 1 |
y |
i 1 |
), |
|
|
k i 1 |
h(x |
i 1 |
|
h y |
i 1 |
k i 1 ) |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||
x |
|
|
x |
|
|
|
h, |
|
|
y |
|
|
y |
|
|
1 |
|
k i |
1 |
k i |
1 |
, |
|
|
|
(i |
1,..., m). |
||||
i |
|
i 1 |
|
|
i |
i |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полагая |
|
|
x0 |
0, |
|
y0 |
1, |
последовательно находим: |
|||||||||||||||||||||||
при |
i |
|
1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
103

k 0 |
|
0.1(0 |
1) |
|
0.1; |
|
k |
0 |
0.1(0 |
0.1 1 |
|
0.1) |
0.12; |
|
|
||||||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
0.1 |
0.1; |
|
|
y |
|
1 |
|
1 |
(0.1 |
|
|
0.12) |
1.11; |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при |
i |
|
2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
0.1(0.1 1.11) |
0.121; |
|
k 1 |
|
0.1(0.1 |
0.1 |
|
1.11 |
|
0.121) |
|
0.1431; |
||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
0.1 |
0.1 |
0.2; |
|
|
y2 |
1.11 |
|
1 |
(0.121 |
|
0.1431) 1.24205. |
|
||||||||||||
|
|
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Аналогично получаем, |
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
i |
3 : |
|
x3 |
0.3; |
y3 |
|
1.398465; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i |
4 : |
|
x4 |
0.4; |
y4 |
1.581804. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Метод Рунге-Кутта |
четвертого |
|
порядка называют классиче- |
|||||||||||||||||||||
ским |
методом Рунге-Кутта, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p 4, c 0, c |
|
c |
1 |
, c |
|
1, d |
d |
|
|
|
1 |
, d |
|
d |
|
1 |
. |
||||||||
2 |
|
4 |
4 |
|
2 |
3 |
|
||||||||||||||||||
|
|
|
1 |
|
3 |
2 |
|
|
|
|
1 |
|
6 |
|
|
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из рекуррентных формул (7.6) получим алгоритм решения задачи Коши классическим методом Рунге-Кутта:
xi xi 1
1 yi 1 6
k1i 1 hf k2i 1
hf k2i 1 hf
hf
k3i 1 hf k4i 1
hf k4i 1 hf
hf
h, |
|
|
yi |
|
yi |
1 |
|
|
yi 1, |
|
(i 1,2,..., m), |
||||
k i 1 |
|
2k i 1 |
2k i 1 |
k i 1 |
, |
||||||||||
1 |
|
|
2 |
|
|
3 |
4 |
|
|||||||
(xi |
1, yi 1 ), |
|
|
|
|
|
|
|
|
|
|||||
(x |
|
|
|
1 |
|
h, y |
|
|
|
1 |
k i 1 ), |
(7.7) |
|||
|
|
|
|
|
|
|
|
||||||||
i |
1 |
|
|
i 1 |
|
|
|
||||||||
|
2 |
|
|
|
2 |
1 |
|
|
|||||||
(xi |
|
|
h |
, yi 1 |
|
1 |
k2i 1 ), |
|
|
||||||
1 |
|
|
2 |
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
(xi |
1 |
h, yi |
1 |
k3i |
1 ) |
(i |
1,2,..., m). |
||||||||
Графиком приближенного решения является ломаная, последовательно соединяющая точки Pi (xi , yi ) (i 0,1,2,.., m) . С уве-
личением порядка численного метода звенья ломаной приближаются к ломаной, образованной хордами интегральной кривой
104

y 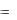 (x) , последовательно соединяющими точками ( xi , (xi ) ) на
(x) , последовательно соединяющими точками ( xi , (xi ) ) на
интегральной кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Решить задачу Коши y x |
y , y(0) 1 |
|||||||||||||||
классическим методом Рунге-Кутта на отрезке |
0;0.4 , с шагом |
|||||||||||||||
h 0.1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Так как f (x, y) |
|
x y , то согласно формулам (7.7) |
||||||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k i 1 |
h(x |
1 |
y |
i |
1 |
), |
|
|
|
|
|
|
|
|||
1 |
i |
|
|
|
|
|
|
|
|
|
|
|
||||
k i 1 |
h(x |
|
1 |
|
h y |
|
|
|
1 |
k i 1 ), |
|
|||||
1 |
|
|
i |
1 |
|
|
|
|||||||||
2 |
i |
2 |
|
|
|
|
|
2 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
k i 1 |
h(x |
|
|
h |
|
y |
|
|
|
1 |
k i 1 ), |
|
||||
1 |
|
|
|
|
|
i 1 |
|
|
|
|||||||
3 |
i |
2 |
|
|
|
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
k4i 1 |
h(xi 1 |
|
h yi 1 |
|
k3i 1 ), |
|
||||||||||
xi xi 1
yi yi 1
h, |
|
|
|
|
||
|
1 |
k i 1 |
2k i 1 |
2k i 1 |
k i 1 |
|
|
|
|||||
6 |
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
||
для |
|
значений |
i 1, 2,3, 4. |
|
|
|
|
|
||||||||
Полагая x0 0, |
y0 |
|
1, |
последовательно находим: |
|
|||||||||||
при |
|
i 1: |
|
|
|
|
|
|
|
|
|
|
||||
k |
|
0 |
|
0.1(0 |
1) |
|
0.1; |
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k |
|
0 |
|
0.1(0 |
0.5 |
|
1 |
0.05) |
|
0.11; |
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
0 |
|
0.1(0 |
0.05 |
1 |
|
0.055) |
0.1105; |
|
||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
0 |
|
0.1(0 |
0.1 |
|
1 |
0.1105) |
0.121050; |
|
||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
0 |
0.1 |
0.1; |
|
|
|
|
|
|
|
|
|||||
y |
|
1 |
|
1 |
(0.1 |
2 |
|
0.11 |
2 |
0.1105 |
0.12105) |
1.110342; |
||||
|
|
|
||||||||||||||
|
1 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при |
|
i |
2 : |
|
|
|
|
|
|
|
|
|
|
|
||
k 1 |
|
0.1(0.1 |
1.110342) |
|
0.1210342; |
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105

k21 0.1(0 0.05 1.110342 0.06604295 0.1320859;
k31 |
0.1(0 |
0.05 |
1.110342 |
0.06604295) |
0.1326385; |
|||||
k41 |
0.1(0 |
0.1 |
1.11342 |
0.1326385) |
0.1442980; |
|||||
x1 |
0.1 |
|
0.1 |
0.2; |
|
|
|
|
|
|
y |
1 |
1 |
(k 1 |
2 |
k 1 |
2 k 1 |
k 1 ) 1.242805. |
|
||
|
|
|||||||||
1 |
|
6 |
1 |
|
2 |
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее получаем при |
|
|
|
|
|
|||||
i |
3 : |
|
x3 |
0.3; |
y3 |
1.399717; |
|
|
||
i |
4 : |
|
x4 |
0.4; |
y4 |
1.583648. |
|
|
||
Для наглядности численные решения одной и той же задачи Коши, рассмотренные в примерах 1-3, сведены в одну таблицу 12.
|
|
|
|
|
|
Таблица 12 |
i |
xi |
Значения yi , |
найденные методом |
Точное ре- |
||
|
|
|
|
|
|
шение |
|
|
|
|
|
|
(x) 2e x x 1 |
|
|
Эйлера |
|
Эйлера- |
Рунге- |
|
|
|
|
|
Коши |
Кутта |
|
|
|
|
|
|
|
|
1 |
0.0 |
1.0 |
|
1.0 |
1.0 |
1.0 |
2 |
0.1 |
1.1 |
|
1.11 |
1.110342 |
1.110342 |
3 |
0.2 |
1.22 |
|
1.24205 |
1.242805 |
1.242805 |
4 |
0.3 |
1.362 |
|
1.39846 |
1.399717 |
1.399718 |
5 |
0.4 |
1.581804 |
|
1.581804 |
1.583648 |
1.583649 |
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Пусть дана система двух дифференциальных уравнений первого порядка:
y1 |
f1 |
(x, y1 |
, y2 ), |
|
|
|
(7.8) |
y2 |
f2 (x, y1, y2 ). |
||
106

Решением системы (7.8) называется пара функций 1(x) и 2 (x) , при подстановке которых в систему получаются тождества.
y1 |
1(x), |
системы уравнений (7.8) |
соответст- |
|
Решению |
|
|||
y2 |
2 (x) |
|
|
|
вует интегральная кривая |
в пространстве |
трех |
измерений |
|
(x, y1, y2 ) . Условия, |
при |
которых через |
каждую точку |
|
P0 (x0 , y10 , y20 ) некоторой области D трехмерного пространства
проходит |
единственная интегральная кривая, содержится в теореме |
||||||||||||||||||||||||||||||||||||||
существования и единственности решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
Теорема. Если функции |
|
f1 (x, y1, y2 ) |
и f2 (x, y1, y2 ) - правые |
||||||||||||||||||||||||||||||
части дифференциальных уравнений системы |
(7.8) – непрерывны |
||||||||||||||||||||||||||||||||||||||
вместе со своими |
|
частными производными по переменным |
|
|
y1 и |
||||||||||||||||||||||||||||||||||
|
|
y2 |
в некоторой области |
D трехмерного пространства, то для |
|||||||||||||||||||||||||||||||||||
любой точки ( x0 , y10 , y20 ) |
D система (7.8) имеет единственное |
||||||||||||||||||||||||||||||||||||||
решение, удовлетворяющее начальным условиям |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 (x0 ) |
|
y10 , y2 (x0 ) |
|
y20 . |
|
(7.9) |
|||||||||||||||||||
|
|
|
|
|
|
Задачи Коши для системы состоит в нахождении решения сис- |
|||||||||||||||||||||||||||||||||
темы (7.8), |
удовлетворяющего начальным условиям (7.9). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Если ввести векторные обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y1 (x) |
|
|
|
|
|
|
|
y1 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 (x,Y ) |
|||||||||||||
|
|
|
|
|
|
Y (x) |
|
|
|
Y (x) |
|
|
f (x,Y ) |
||||||||||||||||||||||||||
|
|
|
|
|
|
y2 (x) |
, |
|
|
y2 (x) |
, |
|
f 2 (x, |
|
) , |
||||||||||||||||||||||||
|
|
|
|
|
|
Y |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y10 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Y0 |
|
|
, то задача Коши (7.8)-(7.9) |
в векторной форме за- |
|||||||||||||||||||||||||||||||||||
|
|
|
y20 (x) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
пишется так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
f (x,Y ) , |
Y (x0 ) |
Y 0 . |
|
(7.10) |
||||||||||||||||||||
|
|
|
|
|
|
Численное решение задачи Коши (7.10) состоит в том, что на |
|||||||||||||||||||||||||||||||||
сетке отрезка |
a, b требуется получить приближенные значения ко- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
в узлах сетки xi (i |
|
1,2,..., m). |
|
|
|
|
|
|
||||||||||||||||||||||||
ординат вектора Y (x) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Обозначим |
вектор, |
аппроксимирующий |
|
|
|
решение |
через |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Yi |
Y (xi ) |
i |
1,2,..., m , |
|
|
|
а |
его |
координаты |
– |
через |
||||||||||||||||||||||||||||
107
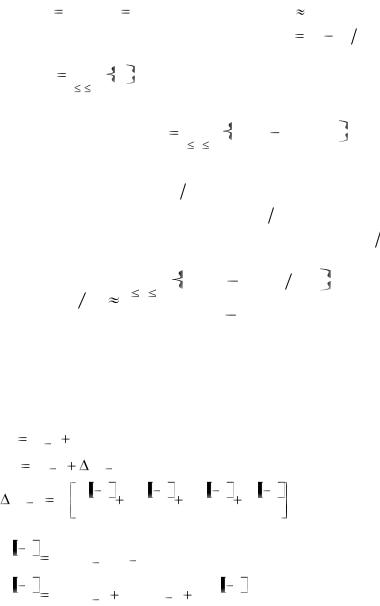
yk i |
(k 1,2; |
i |
|
1,2,..., m) |
так, |
что yk i |
|
yk (xi ) . |
Будем ис- |
||||||||||||
кать решение на равномерной сетке с шагом h |
(b a) m. |
||||||||||||||||||||
|
Величина погрешности численного метода оценивается вели- |
||||||||||||||||||||
чиной d max di |
, |
где di |
- погрешность решения на сетке с ша- |
||||||||||||||||||
|
1 i m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гом h в точке xi |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
di (h) |
max |
|
yk i (h) |
yk (xi ) |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 k |
2 |
|
|
|
|
|
|
|
|
|
|
Практически погрешность в точке xi |
оценивается по формуле |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рунге. Пусть Yi (h) , |
Yi (h 2) |
- |
значение |
численного решения в |
|||||||||||||||||
точке |
xi , полученные для |
шагов |
|
|
h и h 2 соответственно; тогда |
||||||||||||||||
погрешность di |
в |
точке xi |
для |
вычислений с шагом |
h 2 выра- |
||||||||||||||||
жается приближенно равенством |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
max |
yk i (h) |
yk i (h 2) |
|
|
|
||||||||||
|
di (h 2) |
|
|
1 k 2 |
|
|
|
|
|
|
|
|
|
, |
|
(7.11) |
|||||
|
|
|
|
|
|
|
|
|
2 p |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где p - порядок точности численного метода.
Численное решение задачи Коши (7.10) для системы дифференциальных уравнений находится с помощью классического метода Рунге-Кутта четвертого порядка. Векторная форма алгоритма метода Рунге-Кутта для задачи (7.10) соответствует рекуррентным формулам (7.7) и имеет вид:
xi xi 1 h,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y i Y i |
1 |
|
|
Y i |
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
1i 1 |
2 |
|
2i 1 |
2 |
|
3i 1 |
|
4i 1 |
||||
|
Y i 1 |
k |
k |
k |
k |
|||||||||||||||
|
6 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
h f (xi |
1,Y i 1), |
|
|
|
|
|||||||||
|
i |
1 |
|
|
|
|
|
1 |
h, |
|
i 1 |
1 |
|
|
i 1 ), |
k |
h f (xi |
1 |
|
Y |
k |
||||||||||
|
|
2 |
2 |
||||||||||||
2 |
|
|
|
|
|
|
|
|
1 |
||||||
108

|
|
3i 1 |
|
|
|
|
|
h |
|
|
|
||
k |
h f (xi 1 |
,Y |
|||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4i 1 |
|
|
|
|
|
||||||
k |
h f (xi 1 |
h,Y |
|||||||||||
|
|
1 |
|
|
2i 1 ), |
|
|||
i |
1 |
|
k |
|
|||||
2 |
(7.12) |
||||||||
|
|
|
|
|
|||||
|
|
|
|
3i |
1 ) |
|
|||
i |
1 |
k |
(i 1,2,..., m). |
||||||
|
|
|
|
i |
1 |
|
|
|
k ji1 |
1 |
|
|
||
|
|
|
|
|
|
|
( j |
1,2,3,4). |
||||||
где векторы |
k j |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
k ji2 |
1 |
|
|
|
Пример. Найти численное решение задачи Коши для системы |
||||||||||||||
двух дифференциальных уравнений |
|
|||||||||||||
|
|
|
|
|
|
|
y1 |
|
y2 , |
y1 (0) |
0, y2 (0) 1 |
|||
|
|
|
|
|
|
|
y2 |
|
|
y1, |
||||
|
|
|
|
|
|
|
|
|
|
|
||||
на сетке отрезка |
|
0; |
|
|
методом Рунге-Кутта. Вычисления провес- |
|||||||||
|
2 |
|
||||||||||||
ти с шагами |
|
|
и |
|
|
. Оценить погрешность по принципу Рунге. |
||||||||
6 |
|
12 |
||||||||||||
Сравнить численное |
решение |
с |
аналитическим решением |
|||||||||||
|
y1 |
sin x, |
|
y2 |
|
cos x. |
|
|
|
|
|
|
|
|||||||||
|
|
|
Решение. |
Здесь |
|
|
f1 (x, y1, y2 ) |
y2 , |
f2 (x, y1, y2 ) |
y1 , |
||||||||||||
|
x0 |
0, y10 |
|
|
0, |
y20 |
|
1, |
|
h |
6 |
0.5323599. |
|
|||||||||
Численное решение будем искать по формулам (7.12). |
|
|||||||||||||||||||||
Последовательно вычисляя, |
при |
i 1 и j |
1,2,3,4 имеем: |
|
||||||||||||||||||
|
|
0 |
k110 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k1 |
k120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k 0 |
hf (x |
0 |
, y |
, y |
20 |
) |
hy |
20 |
h 1 |
0.523599; |
|
|||||||||||
11 |
1 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
||||||||
k 0 |
hf |
2 |
(x |
0 |
, y , y |
20 |
) |
|
hy |
h 0 0; |
|
|
||||||||||
12 |
|
|
|
|
10 |
|
|
|
|
10 |
|
|
|
|
||||||||
109

k 20
k 30
k 40
Y 1
k 0
21 ; k220
k 0
21 ; k220
k 0
41 ; k420
Y 11
;
Y 22
k 0 |
|
hf (x |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
h, y |
|
|
|
1 |
|
|
k |
0 , y |
|
|
|
|
|
|
1 |
|
|
k 0 ) |
||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
21 |
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
10 |
2 |
|
|
|
11 |
|
|
2 |
|
|
|
12 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
h( y20 |
|
|
1 |
|
k |
0 |
) |
|
|
|
0.52359(1 |
|
0) |
|
|
|
0.52359; |
||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
k 0 |
|
hf |
|
(x |
|
|
|
|
|
|
|
|
1 |
h, y |
|
|
|
|
1 |
k |
0 , y |
|
|
|
|
|
|
|
1 |
|
k 0 ) |
||||||||||||||||||||||||||||||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
10 |
2 |
|
|
|
11 |
|
|
|
2 |
|
12 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
h( y |
|
|
|
|
1 |
|
|
k 0 ) |
|
0.52359 0.26179 |
|
|
|
|
|
0.137078 ; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
10 |
|
|
|
2 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
k 0 |
|
hf (x |
|
|
|
|
|
|
|
|
|
1 |
|
|
h, y |
|
|
1 |
|
k |
0 , y |
|
|
|
|
|
1 |
|
k 0 ) |
||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
31 |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
10 |
2 |
|
|
|
|
|
21 |
|
|
2 |
|
|
|
|
|
22 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
h( y20 |
|
|
1 |
k |
0 |
) |
|
|
|
|
0.52359(1- 0.06853) |
|
|
|
|
|
0.487712; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k 0 |
|
hf |
|
(x |
|
|
|
|
|
|
|
|
1 |
h, y |
|
|
|
|
1 |
k |
0 , y |
|
|
|
|
|
1 |
|
k 0 ) |
||||||||||||||||||||||||||||||||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
10 |
2 |
|
|
|
|
|
21 |
|
|
2 |
|
|
|
|
22 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
h( y |
|
|
|
|
1 |
|
k 0 ) |
|
0.52359 0.26179 |
|
|
|
|
|
|
|
0.137078; |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
10 |
|
|
|
2 |
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
k 0 |
|
hf (x |
|
|
|
|
|
|
|
|
1 |
h, y |
|
|
|
|
|
1 |
|
k |
0 , y |
|
|
|
|
|
|
1 |
|
k 0 ) |
|||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
41 |
|
1 |
|
|
|
|
|
|
2 |
|
|
10 |
2 |
|
|
31 |
|
|
|
2 |
|
|
|
32 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
h( y20 |
|
|
|
1 |
k 0 ) |
0.523599(1- 0.137078) 0.451825; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k 0 |
|
hf |
|
|
(x |
|
|
|
|
|
|
|
|
1 |
h, y |
|
|
|
|
|
|
1 |
k |
0 , y |
|
|
|
|
|
|
|
1 |
k 0 ) |
||||||||||||||||||||||||||||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
42 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
10 |
|
|
|
|
|
|
2 |
|
31 |
|
|
|
2 |
|
32 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
h( y |
|
|
|
|
|
|
|
1 |
k 0 ) |
0.52359 0.48771 |
|
|
|
|
|
0.255366; |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
10 |
|
|
|
|
|
2 |
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y |
|
y |
|
|
|
|
|
|
|
|
|
|
1 |
k |
0 |
|
2k |
|
|
|
|
|
0 |
|
|
2k |
0 |
|
|
|
|
|
|
|
|
|
|
|
k 0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
31 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
11 |
|
|
|
10 |
|
|
|
|
|
|
|
|
6 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
(0.523599 |
|
|
|
2 |
0.523599 |
|
|
2 |
0.487712 |
|||||||||||||||||||||||||||||||||||||||||||||||||
6 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0.4551825) |
|
|
|
|
|
|
|
|
|
0.499674; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
110
