Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2939

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Pn (x2 ) y2 A0 A1 (x2 x0 ) A2 (x2 x0 )(x2 x1 ), т.е.

2h A 2h h

2 y

2h2 A

2 y

;

2h2

2!h2

Аналогично можно найти и другие коэффициенты. Общая

формула имеет вид:

k y0

0,1,2,..., n .

k!hk

Подставляя эти выражения в (2.21),

получим:

P (x)

(x x

)

2 y0

(x x

)(x x )

2!h2

3 y0

)(x

x )(x

)

...

(2.23)

3!h3

n y0

)(x

x )...(x

n 1

n!hn

Данный

многочлен

называется

первым интерполяционным

многочленом Ньютона. Им удобно пользоваться при интерполировании вблизи начальной точки x0 . Конечная разность k y0 может

быть вычислена по формуле (2.20).

Формулу (2.23) часто записывают в другом виде. Для этого

введем	переменную	x	x0	t.	тогда	x x0 th;
			h

x x0	x x0	h	t 1;	x x2	t 2; ... ;	x xn 1	t (n 1).
h	h			h		h

С учетом этого формула (2.23) принимает вид:

P (x

th)

t y

t(t

1) 2

...

t(t

1)...(t n

1) n

(2.23’)

Данное

выражение

может

аппроксимировать

функцию

y f (x) на всем отрезке изменения аргумента

x0 , xn

. Однако с

точки зрения повышения точности расчетов и уменьшения числа слагаемых в (2.23’) ограничиваются случаем t 1. Т.е. ограничиваются случаем x0 x x1 . Для других значений аргумента xi пе-

реписывают соответствующим образом формулу (2.23’), заменив всюду индекс 0 на i .

Многочлены Лагранжа и Ньютона, построенные для одних и тех же узлов интерполяции, тождественно равны между собой (многочлены степени n совпадают в n 1 точке), хотя и имеют различную форму записи.

Формула Ньютона обычно более удобна для применения. Если мы хотим улучшить приближение, повысив степень аппроксимирующего многочлена, добавив несколько новых узлов не меняя старых, то в формуле Ньютона придется добавить только несколько новых слагаемых. Число их равно числу добавленных узлов. В случае формулы Лагранжа надо производить все вычисления вновь.

Частные случаи формулы Ньютона.

1. При n 1 получается формула линейной интерполяции:

P (x)

y y

; y y

t y

При

2 – формула квадратичной интерполяции:

x x

(x x

)(x x )

2 y

P (x)

y y

t(t 1)

2 y0 .

Пример.

Даны

4 значения

функции

x . Вычислить зна-

чение

для

1.73 (таблица 5).

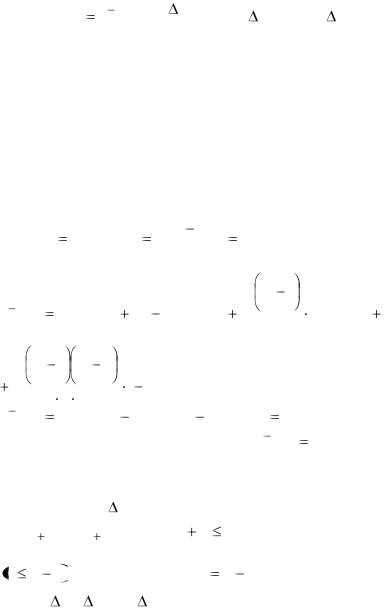
																						Таблица 5
		x					y e x					y						2 y				3 y
							y e x					y						2 y				3 y
	1.72					0.179066
											-0.003546
	1.74					0.175520								+0.000071
											-0.003475											-0.00005
	1.76					0.172045								+0.000068
											-0.003407
	1.78					0.168638
			Каждая последующая конечная разность получается путем
вычитания в предыдущей колонке верхней строки из нижней.
Здесь				h			0.02;		t		1.73		1.72			1	.		По формуле (2.23’) :
Здесь				h			0.02;		t			0.02				2	.		По формуле (2.23’) :
												0.02				2
														1				1		1
										1
e	1.73				0.176066						( 0.003546)				2			2			0.000071
	1.73														2			2
									2									2
									2									2
	1		1		1		1	2

	2		2				2		(		0.000003) .
	2		2				2

			1 2				3
			1 2				3
e	1.73				0.176066				0.001773				0.000009							0.177284.
Восьмизначные таблицы дают значение e 1.73																					0.17728441.
			Интерполяционную формулу (2.23’) обычно используют для

вычисления значений функции в левой половине отрезка. Дело в

том,	разности	k yi вычисляются	через	значения функции
yi , yi	1, ..., yi	k , причем i k n	(2.19’). Поэтому при больших

значениях i мы не можем вычислить разности высших порядков

k n	i .	Например,	при i n 3 в (2.23’) можно учесть
только	y ,	2 y и	3 y .

Для второй	половины рассматриваемого отрезка		разности
лучше вычислить	справа налево. В этом случае t	x	xn	, т.е.
			h

0 и интерполяционный многочлен Ньютона можно получить в

виде:

P(x

th)

t y

t(t

1) 2

...

t(t 1)...(t n 1) n

y .(2.24)

n 1

Данная формула называется интерполяционным многочленом Ньютона.

Мы рассмотрели построение интерполяционного многочлена Ньютона для равноотстоящих узлов. Можно построить многочлен Ньютона, как и в случае многочлена Лагранжа, для произвольного расположения узлов – многочлен с разделенными разностями.

Рассмотрим другие интерполяционные формулы.

1. Многочлен Эрмита. Это - одна из модификаций многочлена Лагранжа. При построении этого многочлена не требуется, чтобы в

узлах xi совпадали с табличными данными не только его значения,

но и их производные до некоторого порядка. В общем случае выражение для многочлена Эрмита очень громоздко, и пользоваться им на практике трудно.

Поэтому ограничиваются лишь некоторыми простейшими случаями. Например, многочлен Эрмита, который сохраняет в двух

точках (x x0 , x1) значения заданной функции, и ее первой

производной.

2. Иногда при выводе интерполяционных формул удобнее использовать не односторонние разности, как для многочлена Ньютона, а центральные, которые содержат разности, лежащие близко к

строке, на которой расположено значение y0 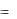f (x0 ) .

На этом основаны формулы Стирлинга и Бесселя. Они м.б. получены различными способами, например, путем преобразования формулы Ньютона. На этом останавливаться не будем. Используемые разности показаны на рисунке 3 для формулы Стирлинга и на рисунке 4 для формулы Бесселя. Эти формулы, вообще говоря, сходятся быстрее, чем формулы Ньютона и Лагранжа. Точность формул Стирлинга и Бесселя приблизительно одинакова. Формула Бесселя дает точный результат при интерполировании близ середи-

ны отрезка (0.25 u

0.75) , а формула Стирлинга – в конце ин-

тервала.

2 y

3 y

4 y

Рис. 4

2 y

3 y

4 y

Рис. 5

Интерполирование периодических функций. Для периодических функций с периодом T 2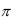целесообразно пользоваться интерполяционной формулой, аналогичной формуле Лагранжа. Выводится она тем же способом и имеет вид:

F (x)

sin(x

x1) sin(x

x2 )...sin(x

xn )

F (x0 )

sin(x0

x1) sin(x0

x2 )...sin(x0

xn )

sin(x

x0 ) sin(x

x2 )...sin(x

xn )

F (x1)

sin(x1

x0 ) sin(x1

x2 )...sin(x1

xn )

.......... .......... .......... .......... .......... .......... .......... ....

sin(x

x0 ) sin(x

x1)...sin(x

xn 1)

F (xn ).

sin(xn

x0 ) sin(xn

x1)...sin(xn

Легко проверить, что

F(x) имеет период

2 .

Точность интерполяции. График интерполяционного много-

члена

y Pn (x)

проходит через заданные точки: значение много-

члена

данной

функции

y f (x)

совпадают в узлах

xi , (i 0,1,..., n) .

Если функция

y f (x) сама является многочленом степени

n , то имеет место тождественное совпадение:

f (x)

Pn (x) . В об-

щем

случае, в

точках,

отличных от

узлов

интерполяции,

R(x)

f (x) Pn (x) 0 .

Эта разность есть погрешность интерполяции, и называется

остаточным членом интерполяционной формулы.

Если функция y

f (x) имеет непрерывные производные до

n 1 порядка включительно, то остаточный член формулы Лагран-

жа имеет вид:
R	L	(x)	(x x0 )(x	x1)...(x xn )	f (n 1) (x ) .	(2.25)

			(n	1)!	*

Здесь производная f (n 1) (x* ) вычисляется в некоторой точке

x x ,

; x

]. Если обозначить

max

f (n 1) (x)

n 1

x0 x xn

то

RL (x)

x0 )(x

x1 )...(x

xn )

M n 1 .

1)!

Остаточный член многочлена Ньютона можно записать в виде

(x)

t(t

1)...(t

(n 1)

(x )h

n 1

x x0

1)!

Если предположить, что разность

n 1 yn постоянна, то

Rn (x)

t(t 1)...(t

(n 1)

y0 .

(2.26)

1)!

Следует подчеркнуть, что существует один и только один интерполяционный многочлен при заданном наборе узлов интерполяции. Формулы Лагранжа, Ньютона и др. порождают один и тот же многочлен (при условии, что вычисления проводятся точно).

Выбор способа интерполяции определяется различными соображениями: точностью, временем вычислений, погрешностями округлений и др. В некоторых случаях более предпочтительной может оказаться локальная интерполяция, тогда как построение единого многочлена высокой степени (глобальная интерполяция) не приводит к успеху.

При построении интерполяционных многочленов с равномерным распределением узлов с увеличением степени многочлена последовательность его значений расходится для любой фиксирован-

ной точки x при 0.7	x	1.
Положение может быть исправлено специальным расположе-
нием узлов интерполяции,		например выбором xi , совпадающими с

корнями многочленов Чебышева степени n 1.

На практике стараются использовать многочлены малой степени (линейную и квадратичную интерполяцию, сплайны).

Подбор эмпирических формул. При интерполировании функций пользуются условием равенством значений многочлена и заданной функции в узлах интерполирования. Это требует высокой точ-

ности данных значений функции yi .

При обработке опытных данных, полученных в результате измерений, нужно иметь в виду ошибки этих данных. Они могут быть вызваны не совершенством измерительного прибора, субъективными причинами, случайными факторами и т.д.

Ошибки экспериментальных данных условно делятся на три категории: систематические, случайные и грубые.

Систематические ошибки обычно дают отклонение в одну сторону от истинного значения измеряемой величины. Их причина и характер известны. Они могут быть вызваны условиями эксперимента, дефектом измерительного прибора и т.д. Эти ошибки устраняются наладкой аппаратуры и введением поправок.

Случайные ошибки определяются большим числом факторов, которые не м.б. устранены или достаточно точно учтены при измерениях или при обработке результатов. Они дают отклонения в ту или другую сторону при повторении измерений. Статистическая обработка экспериментальных данных позволяет определить величину случайной ошибки и довести ее до некоторого приемлемого значения повторением измерений достаточное число раз.

Грубые ошибки явно искажают результат измерений. Они чрезмерно большие и обычно пропадают при повторении опыта.

То есть, экспериментальные данные всегда содержат случайные ошибки. Они, вообще говоря, могут быть уменьшены до сколь угодно малой величины путем многократного повторения опыта. Однако это не всегда целесообразно, т.к. могут потребоваться большие материальные или временные ресурсы.

Значительно дешевле и быстрее можно в ряде случаев получить уточненные данные хорошей математической обработкой имеющихся результатов измерений.

2.4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. ИНТЕГРАЛЬНОЕ ПРИБЛИЖЕНИЕ ФУНКЦИИ ПО СПОСОБУ НАИМЕНЬШИХ КВАДРАТОВ.

Пусть, изучая неизвестную функциональную зависимость между x и y в результате эксперимента получена таблица зна-

чений (таблица 6):				Таблица 6
	x0	x1	x2	…	xn
	y0	y1	y2	…	yn

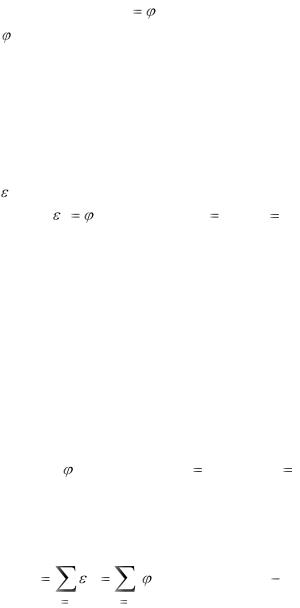
Будем считать, что тип эмпирической формулы выбран, и ее можно представить в виде:

	y	(x, a0 , a1,..., am ) ,	(2.27)
где	- известная функция, а a0 , a1,..., am - неизвестные парамет-

ры. Задача состоит в том, что бы подобрать такие значения этих параметров, при которых эмпирическая формула дает хорошее приближение данной функции.

Как говорилось, здесь не ставится условие (как в случае интерполяции) совпадение опытных данных yi со значениями эмпириче-

ской функции (2.27) в точках xi .

Разность между этими значениями (отклонения) обозначим через i . Тогда

(xi , a0 , a1,..., am ) yi

i 0,1,..., n .

(2.28)

Для нахождения наилучших значений параметров ai требуется

некоторым образом минимизировать эти отклонения. Существует несколько способов решения этой задачи.

1. Простейший – метод выбранных точек. Табличные данные наносятся на координатной плоскости XOY в виде системы точек. За тем проводится простейшая плавная линия (например, прямая) которая наиболее близко примыкает к заданным точкам.

На этой линии выбирают точки, которые, вообще говоря, не принадлежат к исходной системе точек. Число выбранных точек д.б.

равно количеству искомых параметров. Координаты точек (x0j ; y0j )

тщательно измеряют и используют для записи условия прохождения графика функции (2.27) через выбранные точки:

(x0	, a	0	, a ,..., a	m	)	y0	,	j 0,1,..., m.
j		0	1	m		j

Из этой системы уравнений находят значения a0 , a1,..., am .

2. Метод наименьших квадратов. Запишем сумму квадратов отклонений (2.28) для всех точек x0 , x1,..., xn :

[ (x

, a

, a ,..., a

)

]2 .

(2.29)

i 0

Параметры ai формулы (2.27) будем находить из условия минимума функции S S (a0 , a1,..., am ) . В этом состоит метод наименьших квадратов. Т.к. здесь параметры ai выступают в роли

независимых переменных, то ее минимум найдем, приравняв нулю частные производные по этим переменным.

S	0;	S	0; ... ;	S	0 .

a0		a1		am

Получается система уравнений для нахождения a0 , a1,..., am . Чаще всего в качестве эмпирической функции берут много-

член:

(x) a

a x ...

xm .

(2.30)

Формула (2.29) принимает вид:

a x

...

)2 .

(2.31)

1 1

Тогда

a x

...

x m

)

a x

...

x m

)

.......... .......... .......... .......... .......... .......... ......

a x

...

x m

) x m .

Приравнивая эти производные нулю, и собирая коэффици-

енты при неизвестных

a 0 , a1 ,..., a m ,

получаем систему:

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.62 Mб02926.pdf
#
15.11.20222.63 Mб02931.pdf
#
15.11.20222.64 Mб02934.pdf
#
15.11.20222.64 Mб12937.pdf
#
15.11.20222.64 Mб22938.pdf
#
15.11.20222.65 Mб12939.pdf
#
15.11.20222.65 Mб12940.pdf
#
15.11.20222.65 Mб32942.pdf
#
15.11.20222.66 Mб02943.pdf
#
15.11.20222.66 Mб12945.pdf
#
15.11.20222.67 Mб12947.pdf