1383

мации конвективных членов уравнений движения и турбулентности использовалась схема вверх по потоку, для уравнения переноса маркера – схема SuperBee. Шаг по времени выбирался так, что число Куранта не превосходило 0,5. Для апробации выбранной модели турбулентности была проведена серия расчетов с вертикальными решетками.

На рис. 2 показана зависимость осредненного коэффициента потери давления Cl от числа Келегана–Карпентера KC [4]:

где F – сила, действующая на решетку со стороны жидкости,

верхности.

Как видно из данного рисунка, результаты, полученные при помощи модели турбулентности SST k − ω, хорошо согла-

суются с экспериментом.

Рис. 2. Зависимость коэффициента потери давления от числа Келегана–Карпентера; 1 – экспериментальные данные, 2 – модель турбулентности SST k − ω,

3 –модель турбулентности k − ε

51

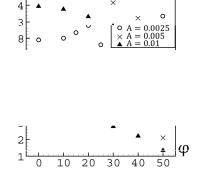
В результате проведенных расчетов была получена зависимость коэффициента потерь давления от угла наклона решеток при различных значениях амплитуды колебаний (рис. 3). Как видно из рисунка, данная зависимость имеет локальный максимум, зависящий от амплитуды колебаний сосуда. Данный факт свидетельствует о том, что при заданной амплитуде существует угол наклона, когда диссипация энергии колебаний жидкости наибольшая (при A = 0,0025 : φmax ≈ 20; A = 0,005 : φmax ≈15 ).

Рис. 3. Зависимость коэффициента потери давления от угла наклона решеток при различных значениях амплитуды колебаний

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-31-00068 мол_а.

Список литературы

1.Wind-induced vibration of tower and practical applications of tuned sloshing damper / K. Fujii, Y. Tamura, T. Sato, T. Wakahara // J. Wind Eng. Ind. Aerodyn. – 1990. – Vol. 33. – P. 263–272.

2.Numerical flow models to simulate tuned liquid dampers: fluid modelling (TLD) with slat screen / M.J. Tait, El A.A. Damatty, N. Isyumov, M.R. Siddique // Journal of Fluids and Structures. – 2005. – Vol. 20 (8). – P. 1007–1023.

52

3.Боталов А.Ю., Родионов С.П. Вынужденные колебания твердого тела с полостью, частично заполненной жидкостью // Вестник Тюмен. гос. ун-та. Физико-математические науки. Ин-

форматика. – 2014. – № 7. – С. 120–26.

4.Tuned liquid dampers with a Keulegan-Carpenter numberdepend screen drag coefficient / J.A. Hamelin, J.S. Love, M.J. Tait, J.C. Wilson // Journal of Fluids and Structures. – 2013. – Vol. 43. – P. 271–286.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ТЕРАПИИ РАКОВОЙ ОПУХОЛИ С ПОМОЩЬЮ НАНОЧАСТИЦ

Д.А. Брацун1, И.В. Красняков2

Пермский национальный исследовательский политехнический университет,

Пермь, Россия, 1bratsun@pspu.ru, 2krasnyakov_ivan@mail.ru

В данной работе рассматривается влияние шума и запаздывания на структурообразование концентрации протеина в квазидвумерной ткани эпителия. В работе дается как стохастическое, так и детерминистское описание системы. Выявлено, что совместное воздействие запаздывания и шума может приводить к возникновению паттернов даже в том случае, когда детерминистское описание предсказывает абсолютную устойчивость.

Ключевые слова: стохастическое моделирование, генная регуляция, запаздывание, биологические системы, сигналы.

Одним из перспективных методов лечения раковых опухолей является терапия наночастицами. В данной статье мы изучаем процесс динамического взаимодействия наночастиц, которые распространяются через лимфатическую систему, с клетками раковой опухоли. Ранее авторы предложили химиомеханическую модель развития раковой опухоли в покровных тканях [1,2] на основе расчета индивидуальной динамики клеток, включая изменение её формы, возможность раздела и интеркаляции. Раковые и нормальные клетки отличаются по регуляции генов и обла-

53

дают различным набором физических и химических параметров. Мы ввели моделирование движения частиц в ткани с учетом их накопления в опухоли, различные варианты взаимодействия опухоли и частиц в зависимости от размера частиц и свойств упругости опухоли. Демонстрируется возможность программного обеспечения для моделирования целенаправленного воздействия наночастицнадинамику опухоли.

Для изучения пространственного влияния внутренних и внешних шумов на регуляцию генов в клеточной системе мы применили многомасштабную химиомеханическую модель, недавно предложенную в [1] для развития опухоли. Эпителий представляет собой эластичный 2D-массив из полигональных клеток с собственной динамикой регуляции генов. Модель позволяет моделировать эволюцию из нескольких взаимодействующих клеток посредством химических сигналов или механически наводящегося напряжения. Алгоритм включает в себя также разделение и интеркаляцию клеток, а также превращение нормальной клетки в раковое состояние, вызванное локальным разрушением пространственной синхронизации клеточных ритмов. Для моделирования задержки индуцированных стохастических химических сигналов мы воспользовались модифицированным алгоритмом Гиллеспи, учитывающим задержки, предложенным в [3].

Список литературы

1.Multiscale modeling of tumor growth induced by circadian rhythm disruption in epithelial tissue / D.A. Bratsun, D.V. Merkuriev, A.P. Zakharov, L.M. Pismen // J. Biol. Phys. – 2016. – 42. – Р. 107–132.

2.Bratsun D., Zakharov A., Pismen L. Modeling of tumour growth induced by circadian rhythm disruption in epithelial tis-

sue // Emergence, Complexity and Computation. – 2015. – Vol. 14. – P. 295–306.

3.Delay-induced stochastic oscillations in gene regulation / D. Bratsun, D. Volfson, J. Hasty, L.S. Tsimring // Proc. Natl. Acad. Sci. U.S.A. – 2005. – 102. – 14593–14598.

54

ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ ПРИ КВАДРАТИЧНОМ НАГРЕВЕ НИЖНЕЙ ГРАНИЦЫ

И ЗАДАННОМ ТЕПЛООБМЕНЕ НА СВОБОДНОЙ ГРАНИЦЕ

С.С. Власова1, Е.Ю. Просвиряков1,2

1Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ, Казань, Россия, sveta040790@yandex.ru

2Институт машиноведения УрО РАН,

Екатеринбург, Россия, evgen_pros@mail.ru

Найдено новое точное стационарное решение системы двумерных уравнений Навье–Стокса в приближении Обербека–Буссинеска, описывающее конвективное движение вязкой несжимаемой жидкости в бесконечном слое при квадратичном распределении температуры при учете теплоотдачи по закону Ньютона–Рихмана на свободной поверхности. Линеаризация данной системы позволяет описать точно течения в точках экстремума температуры и давления. Приведен анализ, зависящий от свойств распределения давления и температуры.

Ключевые слова: точное решение, естественная конвекция, система уравнений Навье–Стокса в приближении Обербека–Буссинеска, закон Ньютона–Рихмана.

Конвекция, связанная с неоднородным нагревом, является одним из самых распространенных видов течений жидкости

игаза во Вселенной. Также конвекция играет большую роль в технических устройствах. Соответственно, объясним непрерывно высокий интерес к конвективным процессам в различных жидкостях. В последнее время интерес к ней стимулируется

иввиду того, что задачи конвекции дают богатый материал для разработки новых идей, касающихся физики происходящих процессов при различных масштабах: от микро- и наноуровней до размеров галактик [1].

При естественной конвекции перемещение вещества происходит исключительно вследствие различия температур в различных местах среды и вызванного им градиента плотностей. Свободная конвекция возникает в поле силы тяжести при неравномерном нагреве (нагреве снизу) текучих веществ. Свободно

55

конвективные течения возникают вследствие изменений плотности, возникающей из-за процессов теплоили массообмена в поле гравитационных сил. Разность плотностей создает выталкивающую силу, под действием которой возникает течение.

Свободная или естественная тепловая конвекция, как

илюбое другое макроскопическое движение жидкости или газа, описывается общей системой уравнений гидродинамики. Эта система включает в себя уравнение движения Навье–Стокса, общее уравнение переноса тепла и уравнение непрерывности, выражающее закон сохранения массы.

Во многих случаях представляет интерес исследование конвекции, протекающей в условиях, когда сжимаемость среды несущественна. В этих случаях исходная система уравнений может быть значительно упрощена.

Соответствующие приближенные уравнения обычно называют уравнениями конвекции в приближении Обербека–Бус- синеска. Основным допущением в приближении Буссинеска является предположение о том, что рассматривается так называемая «слабая» конвекция: вызванные неоднородностью температуры отклонения плотности от среднего значения предполагаются настолько малыми, что ими можно пренебречь во всех уравнениях, кроме уравнения движения, где это отклонение учитывается лишь в члене с подъемной силой [2].

Нахождение точного аналитического решения системы уравнений Навье–Стокса затруднительно ввиду нелинейности системы, зависящей от начальных и граничных условий. Поэтому принципиально важной задачей является нахождение точных классов аналитического решения данной системы.

Чрезвычайно актуальной задачей для многих технических

итехнологических процессов является нахождение значений температуры и давления в точках экстремума гидродинамических полей или около него. Данную проблему можно свести к нахождению экстремальных значений при квадратичном распределении температуры и давления.

56

Была рассмотрена двумерная система Обербека–Буссинес- ка, описывающая естественную конвекцию:

Для решения данной задачи был предложен класс точных решений для описания плоского бесконечного слоя течения вязкой несжимаемой жидкости [3–6]:

Рассмотренная задача была линеаризована и приведена к безразмерному виду с помощью чисел подобия Грасгофа и Прандтля. Приведение к безразмерному виду осуществлялось по двум геометрическим масштабам: поперечному характерному размеру h и продольному характерному размеру l, что является существенным отличием от классических работ.

Еще одним отличием проведенной работы от предыдущих аналитических исследований конвективных течений является теплообмен, учитывающийся на одной из границ слоя, т.е. были рассмотрены граничные условия третьего рода. Нижняя граница слоя жидкости является жесткой. Верхняя граница свободная, но недеформированная. Нагрев осуществляется жесткой грани-

57

цы по квадратичному закону. На свободной границе заданы значения скорости, давления и граничные условия третьего рода. На нижней границе задано условие прилипания.

При анализе точного решения краевой задачи:

которое приведем в общем виде, было отмечено, что линии уровня температуры, давления и скоростей являются кривыми третьего, четвертого и пятого порядка соответственно. Качественное поведение кривых сильно зависит от параметров задачи

ииспользованных числел подобия при линеаризации исходной задачи. Был выведен критерий замкнутости изолиний давления

итемпературы и приведены оценки при которых наблюдаются противотечения в рассматриваемом слое.

Список литературы

1. Гетлинг А.В. Формирование пространственных структур конвекции Рэлея–Бенара // УФН. – 1991. – Т. 161, № 9. –

С. 1–80.

2. Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. – М.: Наука, 1972. – 392 с.

58

3.Аристов С.Н., Шварц К.Г. Конвективный теплообмен при локализованном нагреве плоского слоя вязкой несжимаемой жидкости // Известия Российской академии наук. Механика жидкости и газа. – 2013. – № 3. – С. 53–58.

4.Аристов С.Н., Просвиряков Е.Ю. Об одном классе аналитическихрешенийстационарнойосесимметричнойконвекцииБенара– Марангони вязкой несжимаемой жидкости // Вестник Самар. гос.

техн. ун-та. Сер. Физ.-мат. науки. – 2013. – Вып. 3 (32). – С. 110–118.

5.Аристов С.Н., Просвиряков Е.Ю. Точные решения термокапиллярной конвекции при локализованном нагреве плоского слоя вязкой несжимаемой жидкости // Вестник КГТУ им. А.Н. Ту-

полева. – 2014. – № 3. – С. 3–9.

6.Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теоретические основыхимическойтехнологии. – 2016. – Т. 50, №3. – С. 294–301.

МОДЕЛИРОВАНИЕ ПРОЦЕССА РАЗРУШЕНИЯ ОБРАЗЦОВ СОЛЯНЫХ ПОРОД

С.В. Волегов

Пермский государственный национальный исследовательский университет,

Пермь, Россия, volegov.serg@gmail.com

Вданной работе модернизированный деформационный критерий разрушения использован при численном моделировании в пакете Ansys процесса сжатия образцов соляных пород Верхнекамского месторождения. Представлен анализ развития зон разрушения образцов различной геометрии при помощи коэффициента запаса прочности по деформационному критерию.

Ключевые слова: деформационный критерий разрушения, соляные породы, сжатие образцов, численное моделирование.

Втеории обработки металлов давлением известен критерий разрушения металлов при развитых пластических деформациях [1], использующий понятие предельной пластич-

59

ности. Этот критерий ограничивает накопленную пластическую деформацию (интенсивность деформаций) предельным значением εuпр , зависящим в общем случае от коэффициента жесткости напряженного состояния k, температуры θ, скорости деформирования εu ,

девиатора тензора скорости деформаций.

При переменных величинах коэффициента жесткости, температуры и интенсивности скоростей деформаций в ходе процесса деформирования критерий (1) может быть обобщен в виде интеграла Бейли:

Вариант деформационного критерия разрушения был сформулирован В.Н. Аптуковым для оценки прочности соляных пород в статье [2]. Соляные породы проявляют в некоторых случаях вязкопластические свойства, а в некоторых – хрупкие, в зависимости от характера напряженного состояния. Учитывая этот фактор, деформационный критерий разрушения соляных пород принимается в следующем общем виде:

60