1383

ИССЛЕДОВАНИЕ ДИСЛОКАЦИОННЫХ БАРЬЕРОВ КАК МЕХАНИЗМА УПРОЧНЕНИЯ ПРИ НЕУПРУГОМ ДЕФОРМИРОВАНИИ МОНОКРИСТАЛЛОВ

Н.В. Котельникова, П.С. Волегов

Пермский национальный исследовательский политехнический университет,

Пермь, Россия, natashagreat@rambler.ru

В работе описана математическая модель неупругого деформирования монокристалла. Особое внимание уделено законам упрочнения. Рассмотрено взаимодействие дислокаций, которое может привести, кроме прочего, к образованию барьеров различных типов. Выполнена оценка напряжений, вызываемых поджатыми на барьерах дислокациями. Предложен закон упрочнения, учитывающий как взаимодействие одиночных дислокаций, так и дополнительное упрочнение, создаваемое дислокационными барьерами. В результате моделирования получены значения интенсивностей напряжений, критических напряжений сдвига по системам скольжения и других характеристик, позволяющих описывать и анализироватьпроцесснеупругогодеформированиямонокристалла.

Ключевые слова: монокристалл, упрочнение, физические теории пластичности, неупругое деформирование, дислокационные барьеры.

Эволюция дефектной структуры материала влечёт за собой существенные изменения его макроскопических свойств. Таким образом, управляя мезо- и микроструктурой материала, можно управлять свойствами материала на макроуровне [1]. Следовательно, актуальной задачей является построение математических моделей, учитывающих эволюцию физико-механи- ческих свойств моно- и поликристаллов в процессе неупругой деформации. Это позволит моделировать реальные технологические процессы обработки материалов и прогнозировать свойства образцов после окончания воздействия [2].

Ключевым моментом в работе является описание упрочнения, основанное на методологии физических теорий пластичности [3]. Под упрочнением (на уровне материала) понимают возрастание критических сдвиговых напряжений движения дис-

161

локаций, основной причиной которого (на уровне кристаллической решетки) является образование барьеров, тормозящих движение дислокаций в пределах зерна.

Закон упрочнения описывает скорость изменения критических сдвиговых напряжений на системах скольжения дислокаций (СС), необходимых для продолжения процесса неупругой деформации. В теориях пластичности считается, что это изменение является следствием эволюции микроструктуры материала в процессе деформирования. Существует несколько известных механизмов упрочнения, и их комбинация определяет изменение дефектной структуры материала [4]. В качестве параметров механизмов упрочнения могут выступать накопленные сдвиги, склонность материала к образованию расщепленных дислокаций, учет влияния границ внутри кристалла [5, 6] и т.д. В настоящей работе закон упрочнения рассматривается как совокупность нескольких слагаемых, каждое из которых будет описывать конкретный механизм упрочнения:

где τ(сk ) – скорость изменения критических напряжений на k-й СС. Слагаемое f (k ) описывает «чистое» скольжение полных дис-

локаций и их взаимодействие с препятствиями, включая пересечения дислокаций других СС, и записывается в виде:

где ψ и δ – параметры материала, γ(k ) , τ(ck ) – накопленный сдвиг икритическое напряжение сдвига по k-й СС, τ(ck0) – начальное значение критическогонапряжениясдвига, ai(k ) – модулиупрочнения.

162

В слагаемом fb(k ) в выражении (1) учтено взаимодействие

дислокаций различных СС друг с другом, в результате которого могут образоваться дислокационные барьеры различных типов (Хирта, Ломера–Коттрелла и др.), которые препятствуют движению дислокаций и значительно упрочняют материал. Эти барьеры возникают в результате взаимодействия головных частей расщепленных дислокаций и образования так называемых сидячих дислокаций. Слагаемое, описывающее дополнительное упрочнение, вызванное образованием барьеров, выглядит следующим образом:

где γ*ЭДУ – критическая ЭДУ, N* – число сопряженных СС, ξ1 –

параметр материала, γb0 – начальная плотность барьеров. Помимо включения слагаемого fb(k ) в модель неупругого

деформирования монокристалла важным представляется вопрос оценки напряжений, вызываемых поджатыми на барьерах дислокациями. Известно, что барьеры могут разрушаться, так как каждая поджимаемая дислокация увеличивает напряжение, действующее на барьер. Для оценки напряжений, вызываемых дислокациями, было определено расстояние между дислокациями по СС, «запертой» барьером, а также вычислено предельное количество таких дислокаций, при превышении которого барьер разрушится.

Таким образом, в работе рассмотрена классификация упрочнения, основанная на разделении законов упрочнения на слагаемые, связанные с различными механизмами. Получен конкретный вид этих слагаемых, описывающих упрочнение

163

в монокристалле, вызываемое разными типами взаимодействия дислокаций. Учтены скольжение и накопление как полных, так и расщепленных дислокаций. Также в законе упрочнения учитывается накопление сдвигов и барьеров по СС. Исследован вопрос разрушения барьеров под действием напряжений, вызываемых поджатыми дислокациями.

С использованием разработанной модели проведены численные эксперименты по деформированию монокристалла меди с использованием различных схем деформирования. Выполнены идентификация и верификация модели упрочнения. Проведены расчёты с использованием законов упрочнения, включающих, во-первых, только первое слагаемое в соотношении (1), вовторых, совокупность базового слагаемого и слагаемого, описывающего барьеры. В результате экспериментов установлено, что интенсивность напряжений в модели, учитывающей образование барьеров, повышается на 5–15 %.

Работа выполнена при финансовой поддержке гранта Пре-

зидента РФ № МК-4917.2015.1, РФФИ (грант № 14-01-96008

р_урал_а).

Список литературы

1.Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности: учеб. пособие. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 244 с.

2.Трусов П.В., Волегов П.С. Физические теории пластичности: теория и приложения к описанию неупругого деформирования материалов. Ч. 3: Теории упрочнения, градиентные теории // Вестник Пермского национального исследовательского политехническогоуниверситета. Механика. – 2011. – № 3. – С. 146–197.

3.Trusov P.V., Volegov P.S. Internal variable constitutive relations and their application to description of hardening in single

crystals // Physical Mesomechanics. – 2010. – Т. 13, № 3–4. – С. 152–158.

164

4.Волегов П.С., Янц А.Ю. Несимметричная физическая теория пластичности ГЦК-поликристаллов: особенности численной реализации некоторых схем деформирования // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2011. – № 1. – С. 121–137.

5.Кондратьев Н.С., Трусов П.В. О мере разориентации систем скольжения соседних кристаллитов в поликристаллическом агрегате // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2012. –

№2. – С. 112–127.

6.Кондратьев Н.С., Трусов П.В. Описание упрочнения систем дислокационного скольжения за счет границ кристаллитов в поликристаллическом агрегате // Вестник Пермского национального исследовательского политехнического университета.

Механика. – 2012. – № 3. – С. 78–97.

МОДЕЛИРОВАНИЕ УСТАНОВЛЕНИЯ ТРЕХМЕРНОГО ТЕЧЕНИЯ НЕЛИНЕЙНОЙ ВЯЗКОУПРУГОЙ ЖИДКОСТИ

В ПЛОСКОПАРАЛЛЕЛЬНОМ КАНАЛЕ К.Б. Кошелев1, А.Е. Кузнецов2, Н.А. Макарова2

1Институт водных и экологических проблем СО РАН,

Барнаул, Россия koshelevkb@mail.ru,

2Алтайский государственный технический университет им. И.И. Ползунова,

Барнаул, Россия, mister.tolstykh.m@mail.ru, nmakarova22@gmail.com

Приводятся результаты моделирования течения полимерного расплава в щелевом канале. Исследовано изменение первоначального профиля скорости вдоль оси канала. Также обнаружено наличие вихревых течений в поперечных сечениях.

Ключевые слова: реология, расплавы полимеров, модель Вино- градова–Покровского, трехмерные течения, параллельные вычисления.

В промышленности полимеры перерабатываются в виде растворов и расплавов. При этом большинство процессов переработки происходит в областях со сложной геометрией, когда

165

полимер неоднократно подвергается деформации различных видов. В частности, для контроля качества получаемых изделий важно понимать, как напряжения в полимерной системе, полученные образцом на выходе из одного участка геометрии, будут определять поле скоростей при прохождении следующего [1–2]. Так как с математической точки зрения раствор или расплав полимера представляет собой нелинейную вязкоупругую жидкость, то моделирование установления течения нелинейной вязкоупругой жидкости является актуальной задачей.

В качестве примера рассмотрим течение полимерного расплава в плоскопараллельном канале, когда для описания была выбрана модифицированная реологическая модель Виноградова– Покровского [3–4]. Достоинством этой модели является учет в некотором приближении поведения полимерных молекул. Хотя подобный учет достаточно сложен, но необходим при адекватном моделировании трехмерных течений. В основе модели Виногра- дова–Покровского лежит мезоскопический подход, когда поведение макромолекулы полимера заменяется поведением одного или нескольких релаксаторов, что снижает вычислительную сложность задачи, а переход к макроскопическому описанию осуществляется методами статистической механики.

Далее обсудим расчетную область, представленную на рис. 1. Она представляет собой узкий прямоугольный канал, вдоль оси OZ которого течет расплав полимера. Трехмерный профиль скорости на входе представляет собой параболу при сечении плоскостями XOY и XOZ. Ожидается, что этот профиль будет испытывать деформации ближе к середине канала. Также предполагается, что течение полимера в такой области будет трехмерным [5]: основной поток будет направлен вдоль оси OX, вдоль оси OY будет происходить сильное сжатие потока, что может привести к образованию вихрей, а вдоль оси OZ изменения будут незначительными.

Следует отметить, что основными граничными условиями являются условия прилипания к стенкам (компоненты скорости равны нулю).

166

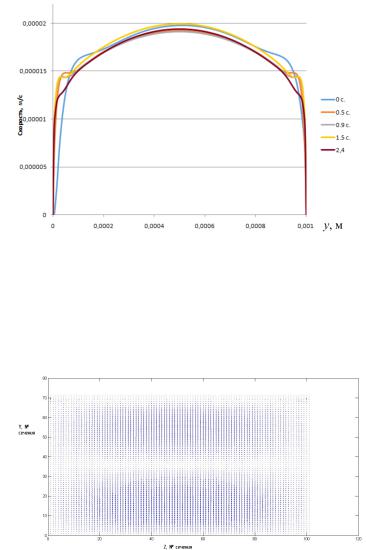
ной отметки. Таким образом, можно констатировать колебания вскоростии постепенное«выравнивание» профиля.

Рис. 2. Графики зависимости скорости о координаты y при значениях времени 0–2,4 с

Не менее важным является также вопрос о присутствии или отсутствии вихрей в поперечном сечении. На рис. 3 показано поле скоростей в сечении, поперечном оси канала, взятом в его середине.

Рис. 3. Скорости потока в поперечном сечении

168

Прежде всего следует отметить, что поперечные компоненты скорости в данном сечении не равны нулю. Это подтверждает гипотезу о трехмерном характере течения такого типа. При этом для выводов о количестве и размерах вихрей и закономерностях их появления следует проводить дальнейшие расчеты.

Список литературы

1.Алтухов Ю.А., Пышнограй Г.В. Входные течения в канале4: 1 текучих линейных полимеров // Механика композиционных материалов иконструкций. – 2001. – Т. 7, №1. – С. 16–23.

2.Гусев А.С., Пышнограй Г.В. Частотные зависимости динамических характеристик линейных полимеров при простом сдвиге // Механика композиционных материалов и конструк-

ций. – 2001. – Т. 7, № 2. – С. 236–245.

3.Кошелев К.Б., Пышнограй Г.В., Толстых М.Ю. Моделирование трехмерного течения полимерного расплава в сходящемся канале с прямоугольным сечением // Изв. РАН. МЖГ. – 2015. – № 3. – С. 3–11.

4.Кошелев К.Б., Пышнограй Г.В., Кузнецов А.Е., Толстых М.Ю. Зависимость гидродинамических характеристик течения полимерного расплава в сходящемся канале от температуры // Механика композиционных материалов и конструкций. – 2016. –

Т. 22, № 2. – С. 175–191.

5.Hertel D., Valette R., Münstedt H. Three-dimensional entrance flow of a low-density polyethylene (LDPE) and a linear lowdensity polyethylene (LLDPE) into a slit die // J. Non-Newtonian Fluid Mech. – 2008. – Vol. 153. – P. 82–94.

169

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СКОЛЬЖЕНИЯ ПО ДУГЕ В ФИГУРНОМ КАТАНИИ

С.О. Краева, Н.С. Шабрыкина1

1Пермский национальный исследовательский политехнический университет,

Пермь, Россия, kraeva.so96@gmail.com

В работе разработана модель скольжения фигуриста по дуге под действием внешних сил. Определена зависимость между угловой скоростью вращения фигуриста, радиусом кривизны траектории движения по дуге и углом наклона тела к вертикали. Предложенная модель будет использоваться для описания захода на вращения и прыжки.

Ключевые слова: биомеханика, фигурное катание.

Применение математического моделирования в изучении процессов, проходящих при выполнении человеком элементов фигурного катания, повышает точность их выполнения и снижает риск возникновения травм. Скольжение по дуге является базовым элементом фигурного катания: оно входит в состав большинства шагов, с него начинаются вращение и прыжки. Поэтому построение математической модели скольжения по дуге необходимо для создания моделей всех ключевых элементов фигурного катания.

Рассмотрим вращение тела фигуриста вокруг неподвижной оси Oz . При этом тело фигуриста движется в плоскости yOz и наклонено к вертикали под некоторым углом α . Тело

касается опоры в одной точке, удаленной от оси на расстояние ρ. В точке контакта с поверхностью действует сила реакции

опоры N = (Nx , Ny , Nz ) . Фигурист движется под действием си-

лы тяжести, приложенной в центре масс тела. Тогда после вычисления сил инерции и применения принципа Даламбера [1], движение описывается системой уравнений:

170