1383

где m – масса тела, ω и ε – угловая скорость и угловое ускорение вращения, (xC , yC ) – координаты центра масс тела, Jz – момент инерции тела относительно оси вращения z , J yz , Jzx –

центробежные моменты инерции относительно осей y, z и z, x соответственно.

Расположение центра масс и моменты инерции зависят от предполагаемой формы тела фигуриста. В данной работе туловище и ноги фигуриста представлены конусом, руки – однородным стержнем, параллельным оси Ox , голова – шаром (рис. 1). Массы и размеры составных частей известны из литературы [2], положение центров масс зависит от угла наклона тела фигуриста к вертикали.

Для данной системы ненулевое значение будет иметь только один из центробежных моментов инерции:

где J yC , JzC – моменты инерции тела относительно собственных

главных осей, проходящих через центр масс.

После преобразований представленной выше системы получаются следующие уравнения:

Nx = 0, Ny = −myC ω2 , Nz = mg , −mgyC + mgρ− J yz ω2 = 0 .

171

ОПИСАНИЕ ВТОРИЧНЫХ ТЕЧЕНИЙ ПОЛИМЕРНЫХ РАСПЛАВОВ НА ОСНОВЕ МЕЗОСКОПИЧЕСКОЙ РЕОЛОГИЧЕСКОЙ МОДЕЛИ

А.Е. Кузнецов1, К.Б. Кошелев2

1Алтайский государственный педагогический университет,

Барнаул, Россия, san-smith@mail.ru,

2Институт водных и экологических проблем СОРАН,

Барнаул, Россия, koshelevkb@mail.ru

Для решения задачи математического моделирования трехмерного течения полимерного расплава в сходящемся плоскопараллельном канале используется модифицированная реологическая модель Виноградова–Покровского, обобщенная для учета немонотонного характера градиентной зависимости вязкости при растяжении. Показано, что максимальное значение скорости наблюдается непосредственно за входом в щелевую часть канала.

Ключевые слова: реология, температурная зависимость, расплавы полимеров, параллельные вычисления, реологическое уравнение состояния, трехмерные течения.

В настоящее время значительный интерес представляет изучение трехмерных течений нелинейной вязкоупругой жидкости в плоскопараллельном канале с внезапным сужением. В данной работе для исследования таких течений применялся метод математического моделирования. В качестве определяющего реологического отношения используется модифицированная реологическая модель Виноградова–Покровского [1–4]. Дискретные аналоги были получены методом контрольного объема с разделением по физическим процессам. Разработка численного алгоритма производилась с учетом возможности его реализации в параллельной форме, с использованием графических процессоров на основе технологии параллельных вычислений CUDA.

Сравнение результатов моделирования проводилось с экспериментальными данными [5]. В работе [5] показано, что для течений полиэтилена низкой плотности существует выраженный вторичный поток в углах проточного канала. Размер и форма этих

174

вихрей различны для разных сечений, параллельных оси канала, что характеризует трехмерный характер поля течения. Кроме того, отмечено, что в исследуемом вихревом течении существует винтовой поток, который направлен к стенкам резервуара. Особое внимание уделено распределению скорости вдоль оси симметрии канала. Обнаружено, что максимальное значение скорости наблюдаетсянепосредственнозавходомв щелевуючастьканала.

Все перечисленные эффекты обнаруживаются при проведении численного эксперимента. На рисунке показано распределение скорости vx (x) вдоль оси канала при температуре 180 °C.

Можно увидеть, что максимальное значение скорости как

врасчетах, так и в эксперименте достигается в непосредственной близости от входа в узкую часть канала (на рисунке вход

вканал обозначен вертикальной линией). Также следует отметить, что профиль скорости в щелевой части канала устанавливается на значительном расстоянии от входа в канал. Это следует учитывать при проведении замеров в узкой части каналов.

Рис. Распределение скорости vx (x) вдоль оси канала при температуре 180 °C

175

Таким образом, в работе продемонстрирована возможность выполнения расчетов в областях со сложной геометрией на базе модифицированной реологической модели Вино- градова–Покровского, проведено сравнение с имеющимися в литературе экспериментальными данными и показано качественное соответствие полученных результатов экспериментальным данным.

Список литературы

1. Алтухов Ю.А., Пышнограй Г.В. Входные течения в канале 4: 1 текучих линейных полимеров // Механика композиционных материалов и конструкций. – 2001. – Т. 7, № 1. –

С. 16–23.

2.Гусев А.С., Пышнограй Г.В. Частотные зависимости динамических характеристик линейных полимеров при простом сдвиге // Механика композиционных материалов и конструк-

ций. – 2001. – Т. 7. № 2. – С. 236–245.

3.Кошелев К.Б., Пышнограй Г.В., Толстых М.Ю. Моделирование трехмерного течения полимерного расплава в сходящемся канале с прямоугольным сечением // Изв. РАН. МЖГ. – 2015. – № 3. – С. 3–11.

4.Зависимость гидродинамических характеристик течения полимерного расплава в сходящемся канале от температуры / К.Б. Кошелев, Г.В. Пышнограй, А.Е. Кузнецов, М.Ю. Толстых //

Механика композиционных материалов и конструкций. – 2016. –

Т. 22. № 2. – С. 175–191.

5. Hertel D., Valette R., Münstedt H. Three-dimensional entrance flow of a low-density polyethylene (LDPE) and a linear lowdensity polyethylene (LLDPE) into a slit die // J. Non-Newtonian Fluid Mech. – 2008. – Vol. 153. – P. 82–94.

176

УПРУГОЕ И НЕУПРУГОЕ ПОВЕДЕНИЕ ПЕРИДОТИТА ПРИ ТРЕХОСНОМ СЖАТИИ

М.А. Кулагина

Кыргызско-Российский Славянский университет, Бишкек, Кыргызская Республика, kulagina_m.a@mail.ru

На основе экспериментальных данных К. Моги [1] рассматривается упругое и неупругое поведение цилиндрических образцов горной породы– перидотита, нагружение которых осуществлялось по двузвенной траектории. Первое звено– гидростатическое сжатие до различного уровня напряжений, второе– приращение осевого давления при постоянном боковом давлении. Установлено приемлемое соответствие между экспериментальнымиирасчетнымиданнымивупругойинеупругойобластях.

Ключевые слова: горные породы, модуль упругости, коэффициент Пуассона, коэффициент разрыхления, предел упругости, предел прочности.

В монографии [1] приведены значения приращения осевого напряжения и соответствующие приращения осевой деформации для второго звена траектории нагружения после гидростатического давления.

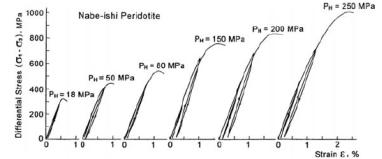
Рис. 1. Экспериментальные зависимости приращения напряжений-приращения деформаций для Nabe-ishi Peridotite

Диаграммы, приведенные на рис. 1, отсканированы и представлены в виде соответствующих табличных значений. Оцифровка графиков была проведена с помощью программы «ChartReader».

177

Как было проверено автором эксперимента, в исходном состоянии перидотит представляет собой изотропный материал. Поэтому для определения упругих констант правомерно использовать обобщенныйзаконГукав следующемвиде:

деформации, εi (i =1,2,3); σj – главные напряжения, σj ( j =1,2,3). Если вид напряженного состояния характеризовать пара-

Предел упругости определялся согласно ГОСТу, по которому угловой коэффициент первоначального линейного участка изменялся на 20 %, проводилась касательная к кривой деформирования с новым угловым коэффициентом, и за предел упругости бралось напряжение в точке касания.

178

где Γ1,Γ2 – главные пластические деформации, λ – коэффициент разрыхления, k – масштабный коэффициент, α – коэффициент, учитывающий кривизну кривой упрочнения.

Данные значения главных деформаций получены с учетом гипотезы В.В. Новожилова о всестороннем равномерном разрыхлении [2].

Для моделирования пластической деформации выдвигаются два предположения:

1) По данным А.Н. Ставрогина [3] после гидростатического давления цилиндрического образца при последующем постоянном боковом давлении с увеличением осевого давления поперечная деформация ε2 соизмерима с осевой деформацией ε1

таким образом, что ε2 = −ε1 на пределе прочности.

2) Γпл2 = −12Γ1пл – условие осесимметричной деформации,

что подтверждается сопоставлением экспериментальных и расчетных данных.

На участке установившейся пластической деформации диаграмма зависимости c(Γ1 ) выполаживается, поэтому с ростом деформации вид напряженного состояния практически не изменяется, параметры λ и k можно считать постоянными для каждого бокового давления.

Рассматривая две точки кривой упрочнения, одна из которых лежит за пределом упругости, а другая является пределом прочности для Р = 150 МПа, из отношения главных деформаций, согласно (3) определяется параметр α путем логарифмирования: α = 2,3 .

Для каждого значения бокового давления на пределе прочности определялись параметры λ и k, исходя из разности главных деформаций:

179

Рис. 2. Экспериментальные и расчетные диаграммы деформирования Nabe-ishi Peridotite при различных боковых давлениях

180