
1383
.pdf
ведущих ученых в российские образовательные учреждения высшегопрофессиональногообразования» подоговору№14.Z50.31.0032.
Список литературы
1.Федотов Е.С., Пальчиковский В.В. Исследование работы резонатора Гельмгольца в волноводе прямоугольного сечения // Математическое моделирование в естественных науках. – 2014. – Т. 1. – С. 268–271.
2.Федотов Е.С., Пальчиковский В.В. Исследование работы резонатора Гельмгольца в волноводе прямоугольного сечения // Вестник Пермского национального исследовательского политехнического университета. Аэрокосмическая техника. – 2014. – № 38. – С. 107–126.
ОБ ОДНОМ ПОДХОДЕ К ОПРЕДЕЛЕНИЮ УСТОЙЧИОВСТИ ПРОЦЕССА НАГРУЖЕНИЯ СТЕРЖНЕВЫХ СИСТЕМ
С РАЗУПРОЧНЯЮЩИМИСЯ ЭЛЕМЕНТАМИ
А.В. Коркин1, В.В. Стружанов2
1Уральский федеральный университет,
Екатеринбург, Россия, alexkorkin@list.ru,
2Институт машиноведения УрО РАН,
Екатеринбург, Россия, stru@imach.uran.ru
Рассматриваются методические аспекты исследования устойчивости градиентных механических систем на примере нагружения одной стержневой системы, элементы которой обладают свойством разупрочнения при растяжении. Методика основана на существенном использовании аппарата математической теории катастроф.
Ключевые слова: стержневая система, разупрочнение при растяжении, равновесие, устойчивость, матрица Гессе, потенциальная функция.
Особенности методики расчета параметров равновесия и определения устойчивости процесса деформирования проиллюстрируем на примере нагружения стержневой системы, пока-
151
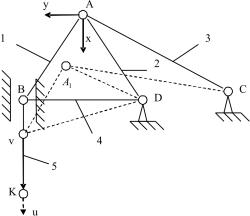
занной на рисунке. Стержни 1, 2, 4 имеют начальную длину l, стержень 3 – длину 2l. При растяжении стержней усилия в них определяются функциями:
Фj |
= Ej ej |
exp |
−e j |
( j = 1,2.4), |
|
||||
|
|
|
ejc |
|
обладающими восходящими и ниспадающими до нуля ветвями. где E j – жесткости стержней при растяжении в упругом состоянии, e j – удлинения стержней, e jc – удлинение, отвечающее
максимальному значению функции Ф. Стержень 2 работает на сжатие и поэтому находится в упругом состоянии, его жесткость
равна E2 . Стержень 5 также упругий с жесткостью при растя-
жении, равной Е. Система деформируется посредством задания монотонно возрастающего перемещения u в точке К (свободному концу стержня 5).
Положение системы определяют обобщенные перемещения: v – вертикальное перемещение точки В, y и x – горизонтальное и вертикальное перемещения точки А (см. рисунок). Тогда x, y, v играют роль параметров состояния системы, а перемещение u – параметра управления.
Рис. Нагружение стержневой системы
152
Запишем теперь выражение для энергии деформации системы:
ε1 |
|
|
−ε |
|
ε3 |
|
|
|
−ε |
|
|
|
|
|
П = E1ε exp( |
|
) dε+ E3ε exp( |
) dε+ |
|||||||||||
|
|
|
||||||||||||
0 |
|
εc1 |
0 |
|
|
|
εc3 |
|
|
|
||||
ε4 |
|
|
−ε |
|
E1ε |
2 |
|
(u − v) |
2 |
E |
|
|||
+ |
E4ε exp( |
) dε+ |
2 |
+ |
|
. |
||||||||
εc4 |
|
|
|
2 |
|
|
|
|||||||
0 |
|
|
2 |
|
|
|
|
|
|
|
||||
Здесь ε1,ε3 ,ε4 – удлинения соответственно стержней 1, 3, 4, а ε2 – укорочение стержня 2. В состоянии равновесия параметры управления и состояния связаны уравнениями [1]:
∂П = 0, |
∂П = 0, |
∂П = 0. |
∂x |
∂y |
∂v |
Представляя функции Фj в виде
Фj |
= Ej (ej − ejn ),ejn |
= ej |
(1− exp |
−e j |
), |
|
|||||
|
|
|
|
ejc |
|
и выделяя линейную и нелинейную части по x, y, v, получаем систему
(E1 + E3 + E2 )x − E1v = |
E1l 3 |
+ |
|
E2l 3 |
+ |
|
E3l 3 |
+ |
||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ E1 (l + ε1n ) |
∂ε1 + E3 (2l + ε3n ) |
∂ε3 + E2 |
∂ε2 , |
|
|
|||||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
∂x |
|
|
||||
(E1 + E3 |
+ E2 ) y = |
E1l |
− |
|
E2l |
− |
|
E3l(1− 13) |
+ |
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
+ E1 (l + |
ε1n ) |
∂ε1 + E3 (2l + ε3n ) |
∂ε3 + E2 |
∂ε2 , |
|
|
||||||||||||||||
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
∂y |
|
|
||||
−E1x + (E1 + E4 + E)v = − |
E1l 3 |
|
+ E1 (l + ε1n ) |
∂ε1 |
+ |
|||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
+ E4 (2l + ε4n ) |
∂ε4 + Eu. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
153
Данную систему нелинейных алгебраических уравнений решаем методом последовательных приближений, применяя схему простой итерации. Сначала для заданного перемещения u нелинейные члены в системе полагаем равными нулю и решаем соответствующую систему линейных уравнений с постоянными коэффициентами, используя, например, метод Гаусса. Находим значения x0, y0, v0, которые являются первым приближением к искомому решению системы. Затем величины x0, y0, v0 подставляем в выражения для нелинейных членов и вычисляем числовые значения правых частей. Получаем систему линейных уравнений, но уже с новыми правыми частями. Ее решение есть x1, y1, v1 (второе приближение). Снова подставляем значения x1, y1, v1 в выражения для нелинейных членов и формируем новые числовые значения правых частей. Решаем линейную систему уравнений, изатемпроцессповторяемнеобходимоечисло раз.
Так как нагружение носит кинетический характер, то итерационный процесс должен сходиться. Проводя вычисления для различных монотонно возрастающих значений параметра u, находим множество точек (u, x, y, v), удовлетворяющих уравнениям данной системы и являющихся критическими точками потенциальной функции П, в которых рассматриваемая механическая система находится в положении равновесия (устойчивом или неустойчивом).
На следующем шаге необходимо из множества критических точек выделить вырожденные критические точки. Для этого выпишем матрицу Гессе потенциальной функции систему (матрицу вторых производных). Ее компоненты:
с |
= |
∂2 П |
, |
с |
= |
∂2 П |
, с |
= |
∂2 П |
, с |
|
= с |
= |
∂2 П |
, |
|||
∂x2 |
∂y2 |
∂v2 |
|
|
||||||||||||||
11 |
|
|
22 |
|
33 |
|
12 |
21 |
|
∂x∂y |
||||||||
|
|
с13 = |
с31 |
= |
∂2 П |
, с23 |
= с32 = |
∂2 П |
. |
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
∂x∂v |
|
|
|
∂y∂v |
|
|
|
||||
154

Теперь для каждой критической точки вычисляем значения компонент матрицы Гессе и находим ее определитель (детерминант матрицы Гессе). Точки, в которых определитель обращается
внуль, являются вырожденными критическими точками*. Здесь и происходит смена типа равновесия. Система приходит в неустойчивое равновесие и происходит скачкообразное изменение параметров состояния. Если же механические параметры системы (свойства стержней) таковы, что гессиан не обращается в нуль ни при каких значениях параметров управления, то деформирование системы происходит равновесно, т.е. при возрастании параметров управления система переходит из одного устойчивого положения
вдругое.
МОДЕЛИРОВАНИЕ ПОЛЕТА МЯЧА С УЧЕТОМ ЭФФЕКТА МАГНУСА
М.С. Корякина
Муниципальное бюджетное общеобразовательное учреждение
«Лицей № 1», Пермь, Россия, mashakorjakina@gmail.com
Рассматривается трехмерная математическая модель движения мяча, брошенного с некоторой высоты с начальной скоростью в поле действия силы тяжести Земли, с учетом эффекта Магнуса и лобового сопротивления воздуха. Изучаются вопросы влияния силы Магнуса на абсолютное твердое тело сферической формы. В рамках построенной модели приводятся аргументы, доказывающие важность учета эффекта Магнуса, сильно влияющего на траекторию полета вращающегося мяча.
Ключевые слова: математическое моделирование, эффект Магнуса, траектория полета мяча.
Работа посвящена изучению влияния эффекта Магнуса на траекторию полета вращающегося мяча. Необходимо разработать математическую модель, позволяющую описать полет ша-
* ГилморР. Прикладнаятеориякатастроф. Кн. 1. – М.: Мир, 1984. – 350 с.
155
рообразного мяча в воздухе с учетом эффекта Магнуса. Модель должна позволять вычислять положение мяча, линейную и вращательную скорости мяча и его ускорение в любой момент времени; описывать траекторию полета мяча при различных начальных условиях.
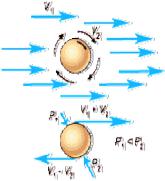
Эффект Магнуса – физическое явление, возникающее при обтекании вращающегося тела потоком жидкости или газа. Образуется сила, воздействующая на тело, зависящая от оси вращения твердого тела и направленная перпендикулярно направлению потока [1]. Вращающийся объект создаёт в среде вокруг себя вихревое движение. С одной стороны объекта направление вихря совпадает с направлением обтекающего потока, и, соответственно, скорость движения среды с этой стороны увеличивается. С другой стороны объекта направление вихря противоположно направлению движения потока, и скорость движения среды уменьшается. Ввиду этой разности скоростей возникает разность давлений (согласно уравнению Бернулли: чем меньше скорость, тем больше давление), порождающая поперечную силу от той стороны вращающегося тела, на которой направление вращения и направление потока противоположны, к той стороне, на которой эти направления совпадают (рис. 1) [2].
Рис.1. Схема, объясняющая возникновение эффекта Магнуса
156
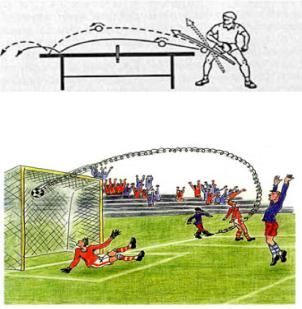
Эффект проявляется на телах вращения и находит свое применение: при разделение смешанных жидкостей на фазы; в конструировании воздушных змеев; в ветроэнергетических установках; в судостроении; в спортивных играх с мячом: например, специальные удары: «топ-спин» в настольном теннисе, «сухой лист» в футболе и т.д. (рис. 2, 3) [2].
Рис.2. Удар «Топ-спин»
Рис.3. Удар «Сухой лист»
Движение мяча может быть описано в соответствии с законами классической механики Исаака Ньютона. Основным законом динамики является второй закон Ньютона, гласящий о том,
что произведение массы тела m на его ускорение a равно равно-
действующей сил Fp , действующих на тело [3]:
|
= ma. |
(1) |
F |
||
p |
|
|
157

Запишем второй закон Ньютона для мяча в векторной форме, расписав равнодействующуювсехсил, действующихнатело:
|
|
|
|
|
= ma, |
|
|
(2) |
|
|
F |
+ F |
+ F |
|
|
||
|
|
тяж |
Магнуса |
сопр |
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
Fтяж |
– сила тяжести, действующая на мяч; |
FМагнуса – сила Маг- |
|||||
нуса, возникающая в результате вращения мяча; |
|
– сила ло- |
||||||
Fсопр |
||||||||
бового сопротивления воздуха.
Запишемформулу длясилы Магнусаввекторнойформе [2]:
|
|
|
|
|
|
|
= |
2π |
ρ |
|
u |
|
v |
|
R2e, |
(3) |
||
|
|
F |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
Магнуса |
3 |
|
|
|
|
|
|
|
|
||||||
где 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– геометрический коэффициент для обтекаемого тела дан- |
||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u – вектор скоро- |
ной формы, ρ – плотность окружающей среды; |
||||||||||||||||||
сти набегающего потока; |
v |
– вектор линейной скорости тела отно- |
||||||||||||||||
сительно невозмущенной среды; R – радиус сферы; e – вектор, за- |
||||||||||||||||||
дающий |
направление силы |
|
Магнуса |
|
|
|
|
угловая скорость |
||||||||||
|
|
(где ω – |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вращениясферы), e = |
|
u |
× |
ω |
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
u |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
Запишем формулы для силы тяжести, действующей на мяч, и силы лобового сопротивления воздуха [3]:
|
|
= mg |
, |
|
|
(4) |
|
F |
|
|
|
||||
тяж |
|
|
|
|
|
|
|
|
= −kv 2 |
|
|
|
|||
|
v |
|
, |
(5) |
|||
Fсопр |
|
|
|||||
|
|
||||||
|
|
|
|
v |
|
|
|
где g – ускорение свободного падения; k – |
коэффициент со- |
||||||
противления, зависящий от формы, размеров, состояния поверхности тела и свойств среды – ее вязкости.
Подставив формулы для сил в выражение (2), получим
158

|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
mg + |
2π |
ρ |
|
u |
|
|
|
v |
|
R2 |
|
u |
ω |
− kv 2 |
v |
= ma. |
(6) |
||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
u |
|
ω |
|
v |
|
|
|
Таким образом, выражение (6) примет следующий вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
mg + |
2π |
ρ |
|
u |
|
|
|
v |
|
R2 |
|
u |
ω |
− kv2 |
v |
= ma. |
(7) |
||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
u |
|
ω |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Используем следующие начальные условия:
x(0) = x0 , y(0) = y0 , z(0) = z0 , vx (0) = v0 x , vy (0) = v0 y , vz (0) = v0 z ,
ωx (0) = ω0x , ωy (0) = ω0 y , ωz (0) = ω0 z ,
где x, y, z – координаты центра масс мяча в момент времени t; x0 , y0 , z0 – начальные координаты центра масс мяча в момент времени t0; vx , vy , vz – проекции вектора скорости мяча на соответствующие оси; v0 x , v0 y , v0 z – проекции вектора скорости в момент времени t0; ωx , ωy , ωz – проекции вектора угловой скорости вращения мяча на соответствующие оси; ω0 x , ω0 y , ω0 z – началь-
ные угловые скорости вращения мяча в момент времени t0.
Во время полета все действующие на мяч силы проходят через его центр масс, поэтому вектор угловой скорости остается постоянным, т.е. угловое ускорение равно нулю.
Результатом данного исследования является получение траектории полета вращающегося мяча с учетом эффекта Магнуса (рис. 4).
Реализовав математическую модель траектории полета мяча, летящего под действием только силы тяжести, т.е. без учета возникновения эффекта Магнуса, можно сравнить полученные результаты. Траектории полетов мяча, представленные на рис. 4, сильно отличаются друг от друга. Таким образом, мы
159
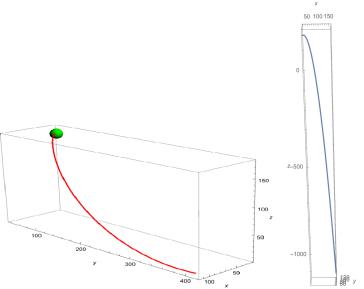
Рис. 4. Траектория полета мяча с учетом эффекта Магнуса
видим, как сила Магнуса сильно влияет на движение мяча и изменяет его траекторию. Очень важно учитывать эффект Магнуса, ведь при пренебрежении данной силой результаты получаются неверные.
Список литературы
1.Прандтль Л. Эффект Магнуса и ветряной корабль // Успехи физических наук. – 1925. – Т. 5, №. 1. – С. 1–27.
2.Эффект Магнуса / И.Д. Бородин [и др.]. – URL: http: //www.rae.ru/forum2012/206/2201.
3.Мякишев Г.Я., Синяков А.З. Физика: Механика. 10 кл. Углубленный уровень: учебник. – 3-е изд., стер. – М.: Дрофа, 2015. – 510 с.
160
