
1383
.pdfСписок литературы
1.Мощенская Е.Ю., Слепушкин В.В. Способ построения кривых ликвидуса двойных эвтектических систем // Журнал не-
орг. химии. – 2015. – Т. 60, № 1. – С. 78–84.
2.Хансен М., Андерко К. Структуры двойных сплавов. Т. I. – М.: Металлургиздат, 1961. – 608 с.
3.Аносов В.Я., Озерова М.И., Фиалков Ю.Я. Основы фи- зико-химического анализа. – М.: Наука, 1976. – 504 с.
4.John A. Dean Lange's Handbook Of Chemistry. – Fifteenth Edition. – McGraw-Hill Education: New York, Chicago, San Francisco, Lisbon, London, Madrid, Mexico City, Milan, New Delhi, San Juan, Seoul, Singapore, Sydney, Toronto. 1999. – 1291 p.
МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ ПОПУЛЯЦИИ МИКРООРГАНИЗМОВ В УСЛОВИЯХ БИОЛОГИЧЕСКОЙ ОЧИСТКИ ПРОМЫШЛЕННЫХ СТОЧНЫХ ВОД
К.К. Мухамбетов1, А.Г. Князева2
1Национальный исследовательский Томский государственный университет,
Томск, Россия, kua3n1404@gmail.com,
2Национальный исследовательский Томский политехнический университет,
Томск, Россия, anna-knyazeva@mail.ru
Исследуется поведение популяции микроорганизмов в условиях очистки сточных вод. Для этого разработана модель, описывающая эволюцию популяции микроорганизмов, которая учитывает их зарождение, гибель и поступление извне. Модель сводится к системе трех дифференциальных уравнений. Осуществлен качественный анализ системы. В рамках модели обнаружено, что существует область значений параметров, при которых популяция микроорганизмов растет, а концентрация загрязняющих химических веществ в воде уменьшается, а также существует область устойчивого существования системы.
Ключевые слова: качественный анализ, биологическая очистка, рост популяции.
241

В настоящее время загрязнение водоемов сточными водами является глобальной проблемой, поэтому особенно важным становится процесс очистки сточных вод. Актуальным направлением в этой сфере является биологическая очистка воды с предварительным озонированием. Озон является сильным дезинфектантом [1]. Также озон является относительно неустойчивым веществом. Распад озона протекает согласно следующей реакции, со скоростью k1 :
2O3 k1 →3O2 .
В модели полагаем, что вода попадает в озонатор, где под действием озона сложные химические соединения, которые далее будем называть исходной органикой, окисляются до более простых, что описывается уравнением
ν A A +ν Φ Φ k →ν S S ,
где Φ – концентрация озона, А – концентрация исходной органики, S – концентрация субстрата, k – скорость реакции, νА , νS и
νΦ – стехиометрические коэффициенты. Простые химические со-
единения или субстрат активно поглощаются микроорганизмами. В модели примем, что озон поступает с постоянной скоростью, концентрация исходной органики постоянна, начальные концентрации микроорганизмов, субстрата и озона известны. Частный случайданноймоделиописанв следующейработе [2].
Динамическая модель будет включать следующие дифференциальные уравнения:
dM |
= μ(S)M − βM 2 ; |
dS |
= kν S Φ − αS μ(S)M ; |
|
|
||
dt |
dt |
||
dΦ = −kν Φ Φ − k1Φ2 + DΦ , dt
здесь M – концентрация микроорганизмов, μ(S) – скорость роста популяции микроорганизмов, β – скорость саморегуляции,
242

αS – параметр, показывающий какая часть субстрата поглощается микроорганизмами, DΦ – скорость поступления озона.
Начальные условия имеют вид:
t = 0 ; M = M0 ; S = S0 ; Φ = Φ0 .
Скорость роста опишем функцией Моно–Гольдани [3, 4]:
μ(S) = μmax ZS + SS+ GS2 ,
где μmax – максимальная скорость роста, ZS – концентрация суб-
страта, при которой скорость роста равна половине максимальной, G – параметр субстратного ингибирования, учитывает негативное влиянияизбыточного количествасубстратанамикроорганизмы.
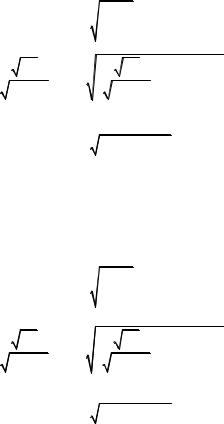
Для удобства анализа запишем систему уравнений в безразмерных переменных:
|
X = |
|
|
|
|
M |
|
; |
Y = |
|
|
|
S |
|
|
|
|
|
|
|
; |
F |
= |
|
|
|
Φ |
|
|
|
; |
|
|
||||||||
|
M0 + S0 + Φ0 |
|
M0 + S0 + Φ0 |
|
|
M0 + S0 + Φ0 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = tμmax . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Тогда система примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
dX |
|
= |
|
|
XY |
|
|
|
− aX 2 ; |
dY |
|
= K |
|
F − α |
|
|
|
|
|
XY |
|
; |
|
|
|
|
|
||||||||||||
|
|
|
|
|
+ Y + gY 2 |
|
S |
S zS + Y + gY 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
dτ |
|
|
|
zS |
|
|
|
|
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dF |
= −KΦ F − LF 2 + dΦ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где a = |
β(M0 + S0 + Φ0 ) |
; |
|
K |
|
= |
kνΦ |
|
|
; |
|
K |
|
|
= |
kνS |
; |
|
|
d |
|
= |
|||||||||||||||||||
|
|
μmax |
|
|
|
|
|
Φ |
μmax |
|
S |
|
|
|
Φ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μmax |
|
|
|
|
|
|
|||||||||||
= |
|
|
|
DΦ |
|
|
; |
zS = |
|
|
|
ZS |
|
|
|
|
|
; |
L = |
|
k1 (M0 + S0 |
+ Φ0 ) |
; |
||||||||||||||||||
μmax (M0 + S0 + Φ0 ) |
|
|
M0 + S0 + Φ0 |
|
|
|
|
μmax |
|
|
|
|
|
|
|||||||||||||||||||||||||||
g = G(M0 + S0 + Φ0 ) |
|
– параметры модели. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
243
Для анализа модели использовались методы, описанные в работах[5, 6, 7]. Былинайденыдвеособыеточкискоординатами:
|
|
|
|
X* = |
KS F* |
|
; |
|
|
|
|
||||
|
|
|
|
αS a |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
( |
αS |
|
− 1) ± ( |
|
|
αS |
|
− 1)2 − 4gzS |
|
|||||
|
aKS F* |
|
|
|
|
|
|
|
|||||||
Y* = |
|
|
|
|
|
|
|
aKS F* |
|
|
; |
||||
|
|
|
|
|
|
2g |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
−K |
Φ |
+ K |
2 + 4Ld |
Φ |
|
|
||||||
|
|
F* = |
|
|
|
|
|
Φ |
|
|
. |
|
|||
|
|
|
|
|
|
|
2L |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Они были исследованы на устойчивость с использованием критерия Гурвица: одна из точек является асимптотически устойчивой, другая – неустойчивой. Неустойчивую точку далее рассматривать не будем. Устойчивая точка покоя имеет координаты:
|
|
|
|
X* = |
KS F* |
|
; |
|
|
|
|
|||
|
|
|
αS a |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
( |
αS |
|
− 1) − ( |
|
αS |
|
− 1)2 − 4gzS |
|
|||||
|
aKS F* |
|
|
|
|
|
|
|||||||
Y* = |
|
|
|
|
|
|
aKS F* |
|
|
; |
||||
|
|
|
|
|
|
2g |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
−K |
Φ |
+ K |
2 + 4Ld |
Φ |
|
|
|||||
|
|
F* = |
|
|
|
|
Φ |
|
|
. |
|
|||
|
|
|
|
|
|
2L |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рисунке представлено изменение концентраций микроорганизмов, субстрата и озона в динамике с начальными условиями X0 = 0,01 ; Y0 = 0,98 ; F0 = 0,01. Кривая 1 описывает
изменение концентрации микроорганизмов; 2 – субстрата; 3 – озона. Из рисунка видно, что в стационарных условиях концентрация микроорганизмов увеличилась, а субстрата, наоборот, уменьшилась по сравнению с начальной.
244
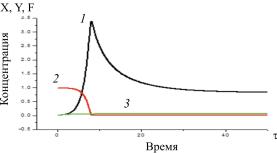
Рис. Зависимость концентраций от времени
Список литературы
1.Предозонирование – как средство интенсификации процессов биологической очистки сточных вод / А.А. Цхе, В.А. Хан, В.Ф. Мышкин, В.П. Колесников, Е.В. Вильсон, Ю.Н. Почуев, А.А. Луканин // Научный журнал КубГАУ. – 2013. – № 87 (03). –
С. 26.
2.Мухамбетов К.К., Князева А.Г, Цхе А.А. Моделирование эволюции популяции микроорганизмов в условиях биологической очистки промышленных сточных вод // Математическое моделирование в естественных науках. – Пермь, 2015. –
Т. 1. – С. 286–290.
3.Математическая биология / Дж. Мюррей, Л.С. Ванаг, А.Н. Дьяконова, Г.Ю. Ризниченко. – Ижевск, 2009. – Т. 1. – 774 с.
4.Марри Дж. Нелинейные дифференциальные уравнения
вбиологии: лекции о моделях / пер. с англ. В.Г. Бабского. – М.:
Мир, 1983. – 396 с.
5.Пантелеев А.В., Якимова А.С. , Босов А.В. Обыкновенные дифференциальные уравнения в приложениях к анализу динамических систем. – М.: Изд-во МАИ, 1997. – 187 с.
6.Методы анализа нелинейных динамических моделей / М. Холодниок, А. Клич, М. Кубичек, М. Марек. – М.: Мир, 1991. – 363 с.
7.Меркин Д.Р. Введение в теорию устойчивости движе-
ния. – М.: Наука, 1987. – 304 с.
245
ИССЛЕДОВАНИЕ ВЛИЯНИЯ РОТАЦИЙ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК НА РАСПРЕДЕЛЕНИЕ ОСТАТОЧНЫХ МЕЗОНАПРЯЖЕНИЙ
В УПРУГОВЯЗКОПЛАСТИЧЕСКОЙ МОДЕЛИ ДЕФОРМИРОВАНИЯ ПОЛИКРИСТАЛЛА
Е.И. Овчинников, П.С. Волегов
Пермский национальный исследовательский политехнический университет,
Пермь, Россия, efm620@gmail.com
В работе рассматривается проблема формирования остаточных напряжений в поликристаллических металлах. В качестве решения предлагается использование математической модели, основанной на физических теориях пластичности. Приведены доводы в пользу использования многоуровневой модели неупругого деформирования поликристаллического агрегата, введено понятие остаточных мезонапряжений. Поставлен вопрос о влиянии ротаций кристаллических решеток на процессы образования остаточных мезонапряжений. Рассмотрены две модели ротаций кристаллических решеток: модель ротаций по Тейлору и модель несовместности пластических деформаций. Проведены численные эксперименты, по результатам которых получены и проанализированы распределения остаточных мезонапряжений при использовании той или иной модели ротаций кристаллических решеток. Сделан вывод о том, что при исследовании остаточных мезонапряжений предпочтительно использовать модель ротаций, учитывающую несовместность пластической деформации.
Ключевые слова: неупругое деформирование, математическая модель, физические теории пластичности, остаточные мезонапряжения, ротации кристаллических решеток.
Производство качественных металлических конструкций и агрегатов сопряжено с большим количеством сложностей; одной из основных является проблема остаточных напряжений, т.е. возникновение напряжений внутри материала или конструкции, существующих в отсутствие внешних нагрузок. Этот вклад может иметь как отрицательное, так и положительное воздействие на характеристики агрегатов и конструкций. Исследование остаточных напряжений является сложной задачей, так как основной причиной появления остаточных напряжений является несовме-
246
стность пластических (а, следовательно, и упругих) деформаций в разноориентированных зернах поликристалла; при этом сам процесс пластической деформации существенным образом зависит от внутренней структуры материала. Исследование же внутренней структуры в натурном эксперименте практически невозможно без нарушения целостности исследуемого объекта. Этим вызвана необходимость разрушать исследуемые объекты, которые зачастую дороги и воспроизведение их затруднено [1].
В настоящее время существует достаточно большое количество методов определения остаточных напряжений [1], они разделяются на два больших класса: механические и физические. Механические методы основаны на разрушении исследуемого образца и оценке проявляющихся остаточных деформаций. Существует большое количество физических (неразрушающих) методов исследования остаточных напряжений, однако их применение достаточнодорогои требуетузкоспециализированногооборудования.
Альтернативой проведению натурных экспериментов является построение математических моделей неупругого деформирования поликристаллических материалов [2]. Проведя анализ экспериментальных методов определения остаточных напряжений, можно сделать вывод о том, что построение точных математических моделей, описывающих состояние и эволюцию внутренней структуры материала в процессе деформирования и последующей разгрузки, может стать решением проблемы определения и описания остаточных напряжений.
Существует большое количество подходов к моделированию процессов деформирования поликристаллических тел. В настоящей работе используется подход, основанный на физических теориях пластичности. Используемые в рамках такого подхода соотношения обладают более прозрачным физическим смыслом, однако включают больше параметров, для которых необходимо разрабатывать процедуры идентификации и верификации [3]. В работе используется конститутивная двухуровневая модель упруговязкопластического деформирования поликристаллического агрегата [4]. В рамках исследования уп-
247
рочнение не рассматривается, поскольку не вносит существенного вклада в вид распределения остаточных напряжений [5].
При моделировании представительного объема удобно ввести в общую классификацию остаточных напряжений по масштабу еще один класс, так называемые остаточные мезонапряжения, уравновешенные на уровне представительного объема и проявляющие себя на масштабах отдельных кристаллитов.
Проведены эксперименты на одноосное растяжение и последующую разгрузку представительного объема поликристалла, состоящего из 1000 зерен, параметры модели соответствуют характеристикам чистой меди. Получены гистограммы распределений зерен поликристалла по величине интенсивности остаточных мезонапряжений. В общей сложности проведено 6 численных экспериментов для двух моделей ротаций до достижения интенсивности деформаций в 50, 75 и 100 %. В таблице представлены отношения среднего значения относительной доли зерен к среднему квадратичному отклонению по классам.
Количественные характеристики распределений ОМН
Отношение среднего значения относи- |
|
Максимальная |
|
||
тельной доли зерен к среднему квадра- |
|
интенсивность |
|
||
тичному отклонению по классам |
|
деформаций, % |
|
||
Используемая модель ротаций |
50 |
|
75 |
|
100 |
По Тейлору |
1,4249 |
|
1,4279 |
|
1,4201 |
Несовместности деформаций |
1,4253 |
|
1,0941 |
|
0,9159 |
На рис. 1 представлены распределения зерен по величине интенсивности остаточных мезонапряжений для модели ротаций по Тейлору, по оси ординат отмечена средняя интенсивность остаточных мезонапряжений каждого класса, по оси абсцисс отмечена удельная доля зерен, входящих в класс.
На рис. 2 представлены аналогичные распределения зерен по интенсивности остаточных мезонапряжений для модели несовместности.
По результатам проведенного исследования можно сделать вывод о том, что при исследовании остаточных напряже-
248
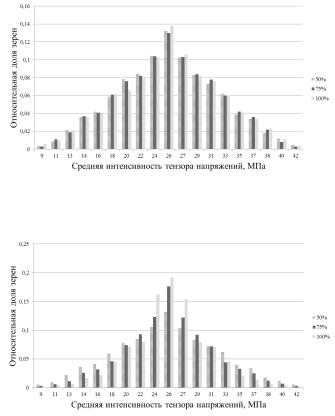
Рис. 1. Распределения кристаллитов по величине остаточных мезонапряжений в экспериментах с учетом модели ротаций по Тейлору
Рис. 2. Распределения кристаллитов по величине остаточных напряжений в экспериментах с учетом модели несовместности пластической деформации
ний предпочтительно использовать модель ротаций, учитывающую несовместность пластических деформаций, так как данная модель позволяет проводить более подробный анализ остаточных мезонапряжений и различать распределения, получаемые при различных пределах деформирования.
Работа выполнена при финансовой поддержке гранта Пре-
зидента РФ № МК-4917.2015.1, РФФИ (грант № 14-01-96008
р_урал_а).
249
Список литературы
1.Methods of measuring residual stresses in components / N.S. Rossinia, M. Dassistia, K.Y. Benyounisb, A.G. Olabib // Materials & Design. – 2012. – Vol. 35. – 572–588.
2.Введение в математическое моделирование / В.Н. Ашихмин, М.Б. Гитман, И.Э. Келлер[и др.]. – М.: Логос, 2004. – 439 с.
3.Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности: учеб. пособие. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 244 с.
4.Trusov P.V., Volegov P.S., Shveykin A.I. Multilevel model of inelastic deformation of fcc polycrystalline with description of
structure evolution // Computational Materials Science. – 2013. – Т. 79. – С. 429–441.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УПРОЧНЕНИЯ В ДВУХФАЗНЫХ МАТЕРИАЛАХ
В.С. Озерных, П.С. Волегов
Пермский национальный исследовательский политехнический университет,
Пермь, Россия, ozernykh@yandex.ru
Вработе рассматриваются некоторые физические механизмы упрочнения поликристаллических материалов. Предложена математическая модель неупругого деформирования представительного объема двухфазного поликристалла с учетом дислокационного упрочнения на границе фаз. Проведено исследование влияния среднего размера зерна
вполикристалле, а также статистического распределения зерен по размерам на деформационное поведение материала. Проведены численные эксперименты при различных схемах нагружения материала, построены и проанализированы кривые деформирования.
Ключевые слова: упрочнение, границы зерен, двухфазные материалы, поликристалл.
Внастоящее время наибольший интерес представляет разработка новых, в том числе функциональных материалов, а также материалов с уникальными свойствами и способов их
250
