1329

ном интервале при i = N определяется из граничных условий в этой точке. С одной стороны,

U N = χ2U N −1 + µN ,

а с другой, по выражению (3.35), –

U N −1 = αNU N + βN .

Из этой системы находится значение функции на последнем интервале разбиения пространственной координаты:

Зная эту величину и используя выражение (3.35), можно рассчитать значения искомой функции на остальных интервалах разбиения i = N −1, N − 2, ..., 1 (обратный ход).

Используя этот метод, необходимо выполнить определённые условия, обеспечивающие устойчивость вычислительного процесса:

первое условие

причём строгое неравенство должно выполняться хотя бы в одной точке;

второе условие

При выполнении этих условий знаменатель выражений (3.41) всегда больше числителя и величина коэффициентов αi оказывается всегда меньше единицы. Поэтому возникшие в процессе расчёта ошибки округления не приводят к их возрастанию и накоплению.

Достоинством метода является минимальное число математических операций, необходимых на его реализацию и, самое главное, линейная зависимость числа операций от числа алгебраических уравнений (порядка 10 операций). Такие методы принято называть экономичными [24]. Это обстоятельство делает метод прогонки весьма популярным для решения уравнений математической физики.

61

Помимо основного варианта метода прогонки разработаны разновидности, применяемые для решения тех же краевых задач, что

идля основного варианта. К ним относятся метод обратной прогонки

иметод встречных прогонок.

Как следует из названия, метод обратной прогонки отличается тем, что вычисление прогоночных коэффициентов η i и ς i произво-

дится в обратной последовательности, начиная с N-интервала для N −1, N − 2, ..., 2,1, с использованием выражения (3.35), а вычисле-

ние функции в прямой последовательности i =1, 2, ..., N − 2, N −1:

Метод встречных прогонок применяется в том случае, если необходимо найти решение в одной из точек исследуемой области. Для этого, исходя из граничных условий при i = 0 , рассчитывают прого-

ночные коэффициенты αi и βi , до исследуемой точки. Затем рассчитываются прогоночные коэффициенты ηi и ς i , исходя из граничных

условий на второй границе при i = N . Записываются выражения искомой величины в исследуемой точке:

Совместное решение этой системы позволяет определить значение искомой функции в точках i и i +1 . При необходимости значения функции в других точках исследуемой области рассчитываются по любому из приведённых выражений (3.46). Для реализации метода здесь и далее использован пакет MATLAB [29].

Пример 3.1. Решение краевой задачи методом прогонки. На ин-

тервале [0,1] решим краевую задачу методом прогонки:

Y ′′ − 2 XY ′ − 2Y = −4 X ; Y (0) − Y ′(0) = 0; Y (1) = 1 + e = 3, 71828,

и сравним решение, полученное численным методом, с аналитическим решением [28]

Y = X + exp (х2 ) .

62

Для решения задачи исследуемую область разбиваем на N =10 интервалов величиной

h x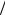 =1 N =1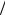10 = 0,1.

Дифференциальные операторы уравнения заменяем конечноразностными выражениями:

Преобразуя эти выражения, получим систему трёхчленных алгебраических уравнений для каждого из интервалов разбиения пространственной координаты:

i =1, 2, ..., N −1 .

Записываем значение искомой функции на каждом интервале разбиения пространственной координаты

Y i = α i +1Y i +1 + β i +1 ; i = N −1, N − 2, ..., 2,1.

63

Программа решения краевой задачи:

n=10; hx=1./n; for j=1:n

x(j)=hx*j; a(j)=1.+x(j)*hx; b(j)=1.-x(j)*hx; c(j)=2.+2.*hx^2; f(j)=4.*x(j)*hx^2; end

alf(2)=1./(1.+hx); bet(2)=0.; for j=2: n

r1=c(j)-a(j)*alf(j); alf(j+1)=b(j)/r1; bet(j+1)=(a(j)*bet(j)+f(j))/r1; end

y(n+1)=3.71828; for j=n:-1:1

y(j)=alf(j+1)*y(j+1)+bet(j+1); end

for j=1:n+1

x(j)=hx*(j-1); x1=x(j)^2; x3=exp(x1); xx(j)=x(j)+x3; end

disp(y); disp(xx);

Результаты расчета приведены в табл. 3.1, 3.2.

Таблица 3 . 1

Коэффициенты системы трёхчленных алгебраических уравнений в зависимости от пространственной координаты

64

Таблица 3 . 2

Прогоночные коэффициенты, значения искомой функции и погрешность численного решения

3.2.2. Циклическая прогонка

Большинство электрических машин имеют замкнутый магнитопровод. Исследование магнитных полей таких машин производится в цилиндрической системе координат. Для задач, решаемых в цилиндрической системе координат, широко используется вариант прогонки, называемый циклическим [27].

Характерной особенностью таких задач являются условия периодичности для коэффициентов уравнений и решения задачи:

а также для них справедливы периодические краевые условия в точках сопряжения

i = 0,1, 2, ..., N −1 и сформулировать её в виде:

65

Будем искать решение как сумму составляющих

где Ui – решение неоднородной задачи с однородными краевыми условиями:

U 0 = 0; U N = 0;

Vi – решение однородной задачи с неоднородными краевыми условиями:

V 0 =1; V N =1.

В полном соответствии систем (3.51) и (3.52) краевой задаче (3.49) можно убедиться, умножив (3.52) на YN и сложив с (3.51).

Каждая из краевых задач (3.51) и (3.52) решается методом прогонки, описанным выше:

Для реализации циклической прогонки необходимо затратить 14N–8 математических операций на один интервал разбиения пространственной координаты, т.е. этот метод также является экономичным. При соблюдении условий устойчивости прогонки накопления ошибки не происходит, счёт является устойчивым.

66

Пример 3.2. Решение периодической задачи методом цикличе-

ской прогонки. В области [0, 2π ] решим краевую задачу

∂2Y − 0, 446Y = − f (x)

∂x2

спериодическими краевыми условиями

Правая часть дифференциального уравнения является функцией пространственной координаты и для 24 интервалов имеет следующие значения:

Исследуемая область разбивается на N = 24 пространственных интервалов величиной

h x = 2π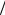 N = 0, 2618 .

Дифференциальный оператор аппроксимируетcя конечно-раз- ностным выражением со вторым порядком точности и подставляется в уравнение

Y i +1−2Y i +Y i −1 − 0, 446Yi = − fi .

2

hx

Преобразуя это выражение, получаем систему трёхчленных алгебраических уравнений для всех интервалов разбиения пространственной координаты:

67

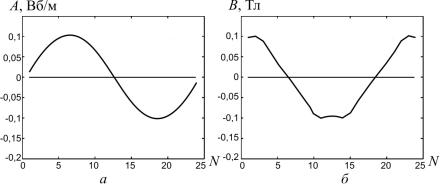
По полученным данным построены графические зависимости A( x) = Y ( x) и B(x) = Y ′(x) , которые описывают распределение век-

торного потенциала и магнитной индукции по длине расточки стато-

ра (рис. 3.2).

Рис. 3.2. Пространственное распределение векторного потенциала (a) и магнитной индукции (б)

Программа решения краевой задачи:

n=24; dx=2.*pi/n;

a(1:n+1)=1.; b(1: n+1)=1.; c(1: n+1)=a(1: n+1)+b(1: n+1)+0.446*dx^2; f(1:n+1)=0; r1=0.137*dx^2; f(3:10)=r1; f(15:22)=-r1; ss(1:n)=0.;

alf(2)=0.; bet(2)=0.; gam(2)=1.;

disp(a); disp(b); disp(c); disp(f); disp(alf); disp(bet); disp(gam);

68

for j=1:n nn(j)=j;

end

for j=2:n+1

r=c(j)-a(j)*alf(j); alf(j+1)=b(j)/r; bet(j+1)=(f(j)+a(j)*bet(j))/r; gam(j+1)=a(j)*gam(j)/r;

end

u(n)=bet(n+1); v(n)=alf(n+1)+gam(n+1); for j=n-1:-1:2

u(j)=alf(j+1)*u(j+1)+bet(j+1); v(j)=alf(j+1)*v(j+1)+gam(j+1); end

r2=bet(n+2)+alf(n+2)*u(2); r3=1.-alf(n+2)*v(2)-gam(n+2); y(n+1)=r2/r3; y(1)=y(n+1);

for j=2:n y(j)=u(j)+y(n+1)*v(j);

end

bl(1)=(y(2)-y(n))/(2.*dx); bl(n)=(y(1)-y(n-1))/(2.*dx); for j=2:n-1

bl(j)=(y(j+1)-y(j-1))/(2.*dx); end

n1(nn)=nn; n2(nn)=ss; n3(nn)=bl(1: n); n4(nn)=y(1: n); disp(y); disp(bl);

plot(n1,n2,n1,n3,n1,n4)

Результаты решения задачи приведены в табл. 3.3, 3.4.

Таблица 3 . 3

Коэффициенты системы алгебраических уравнений и прогоночные коэффициенты

69

Окончание табл. 3 . 3

Таблица 3 . 4

Коэффициенты U(J), V(J) и результаты решения краевой задачи Y(j) и BL(j)

70