
1329
.pdf
Таблица 5 . 5
Решение краевой задачи
j |
|
|
|
|
i |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
|||||||||
1 |
0,0149 |
0,0298 |
0,0446 |
0,0589 |
0,0720 |
0,0828 |
0,0901 |
0,0927 |
|
2 |
0,0298 |
0,0597 |
0,0896 |
0,1189 |
0,1462 |
0,1692 |
0,1849 |
0,1906 |
|
3 |
0,0446 |
0,0896 |
0,1353 |
0,1810 |
0,2248 |
0,2629 |
0,2899 |
0,2996 |
|
4 |
0,0589 |
0,1189 |
0,1810 |
0,2450 |
0,3090 |
0,3678 |
0,4119 |
0,4283 |
|
5 |
0,0720 |
0,1462 |
0,2248 |
0,3090 |
0,3983 |
0,4876 |
0,5616 |
0,5897 |
|
6 |
0,0828 |
0,1692 |
0,2629 |
0,3678 |
0,4876 |
0,6225 |
0,7574 |
0,8072 |
|
7 |
0,0901 |
0,1849 |
0,2899 |
0,4119 |
0,5616 |
0,7574 |
1,0384 |
1,1241 |
|
8 |
0,0927 |
0,1906 |
0,2996 |
0,4283 |
0,5897 |
0,8072 |
1,1241 |
1,2217 |
|
9 |
0,0901 |
0,1849 |
0,2899 |
0,4119 |
0,5616 |
0,7574 |
1,0384 |
1,1241 |
|
10 |
0,0828 |
0,1692 |
0,2629 |
0,3678 |
0,4876 |
0,6225 |
0,7574 |
0,8072 |
|
11 |
0,0720 |
0,1462 |
0,2248 |
0,3090 |
0,3983 |
0,4876 |
0,5616 |
0,5897 |
|
12 |
0,0589 |
0,1189 |
0,1810 |
0,2450 |
0,3090 |
0,3678 |
0,4119 |
0,4283 |
|
13 |
0,0446 |
0,0896 |
0,1353 |
0,1810 |
0,2248 |
0,2629 |
0,2899 |
0,2996 |
|
14 |
0,0298 |
0,0597 |
0,0896 |
0,1189 |
0,1462 |
0,1692 |
0,1849 |
0,1906 |
|
15 |
0,0149 |
0,0298 |
0,0446 |
0,0589 |
0,0720 |
0,0828 |
0,0901 |
0,0927 |
Окончание табл. 5 . 5
j |
|
|
|
i |
|
|
|
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||
|
||||||||
1 |
0,0901 |
0,0828 |
0,0720 |
0,0589 |
0,0446 |
0,0298 |
0,0149 |
|
2 |
0,1849 |
0,1692 |
0,1462 |
0,1189 |
0,0896 |
0,0597 |
0,0298 |
|
3 |
0,2899 |
0,2629 |
0,2248 |
0,1810 |
0,1353 |
0,0896 |
0,0446 |
|
4 |
0,4119 |
0,3678 |
0,3090 |
0,2450 |
0,1810 |
0,1189 |
0,0589 |
|
5 |
0,5616 |
0,4876 |
0,3983 |
0,3090 |
0,2248 |
0,1462 |
0,0720 |
|
6 |
0,7574 |
0,6225 |
0,4876 |
0,3678 |
0,2629 |
0,1692 |
0,0828 |
|
7 |
1,0384 |
0,7574 |
0,5616 |
0,4119 |
0,2899 |
0,1849 |
0,0901 |
|
8 |
1,1241 |
0,8072 |
0,5897 |
0,4283 |
0,2996 |
0,1906 |
0,0927 |
|
9 |
1,0384 |
0,7574 |
0,5616 |
0,4119 |
0,2899 |
0,1849 |
0,0901 |
|
10 |
0,7574 |
0,6225 |
0,4876 |
0,3678 |
0,2629 |
0,1692 |
0,0828 |
|
11 |
0,5616 |
0,4876 |
0,3983 |
0,3080 |
0,2248 |
0,1462 |
0,072 |
|
12 |
0,4119 |
0,3678 |
0,3090 |
0,2450 |
0,1810 |
0,1189 |
0,0589 |
|
13 |
0,2899 |
0,2629 |
0,2248 |
0,1810 |
0,1353 |
0,0896 |
0,0446 |
|
14 |
0,1849 |
0,1692 |
0,1462 |
0,1189 |
0,0896 |
0,0597 |
0,0298 |
|
15 |
0,0901 |
0,0828 |
0,0720 |
0,0720 |
0,0446 |
0,0446 |
0,0149 |
121
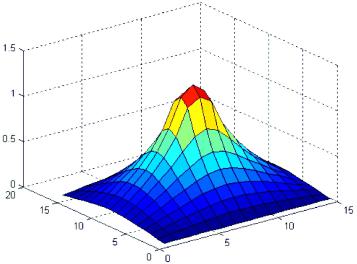
Рис. 5.1. Пространственное распределение решения краевой задачи
Значения искомой функции, полученные при решении полевой задачи, полностью соответствуют установившимся значениям решения нестационарных задач, рассмотренных в главе 4.
Графическое изображение результатов решения двумерной краевой задачи представлено на рис. 5.1.
5.2.МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ УРАВНЕНИЙ
СПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
При решении краевых задач наиболее часто встречаются уравнения с переменными коэффициентами вида
∂ |
|
|
∂ |
U |
|
∂ |
|
|
∂ |
U |
|
|
||||
|
|
K 1 |
( x, y ) |
|
|
|
+ |
|
|
|
K 2 |
( x, y ) |
|
|
− q ( x, y )U = |
f (x, y) . (5.28) |
∂ |
|
∂ |
|
|
|
|
|
|||||||||
x |
|
x |
∂ |
y |
∂ |
y |
|
|
||||||||
Уравнение дополняется условиями на границах, образующих совместно с уравнением краевую задачу.
122
Указанное уравнение может быть решено конечно-разностными методами. Для этого дифференциальные операторы заменяются ко- нечно-разностными выражениями в виде
|
|
|
1 |
|
U i+1, j −U i, j |
|
U i, j −U i−1, j |
|||||||||
|
|
|
|
K i+0,5, j |
|
|
|
− K i −0,5, j |
|
|
|
|
+ |
|||
|
|
|
|
hx |
|
hx |
|
|||||||||
|
|
|
hx |
|
|
|
|
|
|
|
||||||
|
1 |
|
U i, j +1 |
−U i, j |
|
|
U i, j −U i, j −1 |
(5.29) |
||||||||
+ |
− K i, j −0,5 |
− qi, jU i, j = f i, j, |
||||||||||||||
|
K i, j +0,5 |
|
|
|
|
|
|
|
||||||||
|
h y |
h y |
|
|||||||||||||
|
h y |
|
|
|
|
|
|
|||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K i +0,5, j = K ( x + 0, 5h x, y ) ; |
K i −0,5, j |
= K ( x − 0,5h x, y ) ; |
||||||||||||
|
|
K i, j +0,5 = K ( x, y + 0,5h y ) ; |
K i, j −0,5 = K ( x, y − 0,5h y ) , |
|||||||||||||
|
|
|
|
|
|
i =1, 2, ..., N1 ; |
j =1, 2, ..., N 2 . |
|||||||||
Преобразовывая полученные выражения при естественной нумерации неизвестных, приходим к системе пятичленных алгебраических уравнений, записываемых в виде
Ai , jU i −1, j + Bi , jU i +1, j + C i , jU i, j −1 + D i , jU i , j +1 − E i , jU i, j = F i , j ,
i =1, 2, ..., N1 ; j =1, 2, ..., N 2 . |
(5.30) |
Особенностью этой системы является следующее. Во-первых, большая размерность системы: число её неизвестных равно Np, где p – число координат исследуемой области. В частности, для рассматриваемого уравнения (5.28) число неизвестных равно N1 N2. Во-вторых, матрица системы оказывается слабо заполненной. В каждой строке матрицы отлично от нуля лишь незначительное число элементов: при решении плоскопараллельной задачи число отличных от нуля элементов равно пяти, а для объёмных задач – семи. Матрица системы имеет ограниченное число диагоналей с ненулевыми элементами (рис. 5.2). Для уравнений второго порядка с постоянными и переменными коэффициентами (5.28) матрица является симметричной и положительно определённой. В этом случае элементы диа-
123
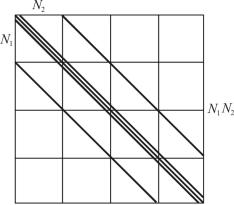
гоналей, расположенных сим-
|
метрично |
относительно |
глав- |
|
|
ной, имеют одинаковые значе- |
|||
|
ния, а все миноры системы по- |
|||
|
ложительны. Для |
уравнений |
||
|
других видов эти условия мо- |
|||
|
гутневыполняться. |
|
|
|
|
Полученная |
система |
||
|
с учётом граничных условий |
|||
|
может быть решена извест- |
|||
|
ными методами: |
прямыми |
||
|
и итерационными. Ввиду зна- |
|||
Рис. 5.2. Матрица системы пятичленных |
чительной |
размерности |
по- |
|
алгебраических уравнений |
лученной системы алгебраи- |
|||
ческих уравнений приходится использоватьспециальные методы, учитывающие её особенности. Если, например, использовать
для решения хорошо известный метод Гаусса, то число математических операций будет равно приблизительно 2/3 (N1 N2)3.
При этом, однако, большая часть операций является несодержательной, так как проводится над нулевыми элементами. Поэтому метод Гаусса применяется лишь для решения систем малой размерности. Чаще всего для подобных систем уравнений используются методы факторизации с исключением несодержательных операций. Эти методы используют возможность представления прямоугольных матриц в виде произведения треугольных и диагональных матриц [25, 27]. Решение системы, таким образом, сводится к последовательному решению систем с треугольными матрицами, что даёт значительное уменьшение числа математических операций. Для систем с симметричными матрицами рациональнее всего использовать метод квадратного корня, который помимо уменьшения число математических операций, позволяет также сократить объём используемой для решения машинной памяти. Подробно ознакомиться с этими методами можно в указанной выше литературе, а программы, реализующие эти методы, достаточно широко представлены в математических пакетах
ЭВМ (Matkad, MATLAB и др.).
124
В качестве примера решения двумерной краевой задачи конеч- но-разностным методом рассмотрим приведённое выше решение уравнения Пуассона.
Пример 5.2. Решение двумерной краевой задачи конечно-раз-
ностным методом. В квадрате [0:1,0:1] решим стационарную краевую задачу
∂ 2U |
+∂ |
2U |
= f (x, y) |
|
∂ x2 |
∂ y2 |
|||
|
|
при нулевых граничных условиях
U (0, y) = U (1, y) = U (x,0) = U (x,1) = 0 .
Примем при решении краевой задачи ту же плотность источников fi, j , что и в примере 5.1.
Пространственные координаты x и y разбиваем на N1 = N2 = N =16 интервалов величиной h =1/ N = 0, 0625 .
Дифференциальные операторы аппроксимируем конечно-раз- ностными выражениями и после преобразования получим систему алгебраических уравнений:
Ai, jU i−1, j + Bi, jU i+1, j + C i, jU i, j −1 + +Di, jU i, j +1 − E i, jU i, j = F i, j,
i=1, 2, ..., N 1 −1;
j=1, 2, ..., N 2 −1,
где Аi, j = Вi, j = Сi, j = Di, j =1; Ei, j = 4; Fi, j = fi, j h2
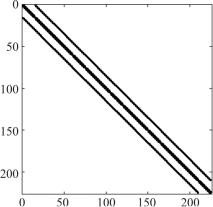
Матрица коэффициентов полученной системы алгебраических уравнений представлена на рис. 5.3.
Рис. 5.3. Матрица реальной системы алгебраических уравнений краевой задачи
125
Полученную систему алгебраических уравнений решаем с использованием известных численных методов [29].
Программа решения двумерной краевой задачи конечно-раз- ностным методом:
n1=17; n2=17; dn=16; hx=1./(n1-1); hy=1./(n2-1); dt=0.001; a(1:225,1:225)=0; f(1:225)=0; f(97:99)=-100.*hx^2; f(112:114)=-100.*hx^2; f(127:129)=-100.*hx^2; i1=17; i2=29;
while i1<212 |
|
|
for i=i1:i2 |
|
|
a(i,i-15)=1.; a(i,i-1)=1.; |
a(i, i)=-4.; |
a(i,i+1)=1.; a(i,i+15)=1.; |
end |
|
|
i1=i1+15; i2=i2+15; |
|
|
end |
|
|
for i=16:15:196 |
|
|
a(i,i-15)=1.; a(i,i)=-4.; a(i,i+1)=1.; |
a(i,i+15)=1.; |
|
end |
|
|
for i=30:15:210 |
|
|
a(i,i-15)=1.; a(i,i-1)=1.; |
a(i,i)=-4.; |
a(i,i+15)=1.; |
end
for i=2:14
a(i,i-1)=1.; a(i,i)=-4.; a(i,i+1)=1.; a(i,i+15)=1.;
end
for i=212:224
a(i,i-15)=1.; a(i,i-1)=1.; a(i,i)=-4.; a(i,i+1)=1.; end
a(1,1)=-4.; a(1,2)=1.; a(1,16)=1.; a(15,15)=-4.; a(15,14)=1.; a(15,30)=1.; a(211,212)=1.; a(211,211)=-4.; a(211,196)=1.; a(225,225)=-4.; a(225,224)=1.; a(225,210)=1.;
x=f/a;
disp(x);
Результаты решения краевой задачи приведены в табл. 5.6. Результат решения краевой задачи конечно-разностным методом
совпадает с результатом её решения методом разделения переменных. При высоких порядках системы алгебраических уравнений их решение прямыми методами требует значительных затрат машинного времени. Для решения подобных систем более рациональными являются итерационные методы, позволяющие упростить процесс решения, уменьшить занимаемую память, а в ряде случаев сократить
время решения.
126

Таблица 5 . 6
Решение краевой задачи
j |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||
|
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
6 |
|
7 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
0,0149 |
|
0,0298 |
|
0,0446 |
|
0,0589 |
|
0,0720 |
|
0,0828 |
|
0,0901 |
|
0,0927 |
|||
2 |
|
0,0298 |
|
0,0597 |
|
0,0896 |
|
0,1189 |
|
0,1462 |
|
0,1692 |
|
0,1849 |
|
0,1906 |
|||
3 |
|
0,0446 |
|
0,0896 |
|
0,1353 |
|
0,1810 |
|
0,2248 |
|
0,2629 |
|
0,2899 |
|
0,2996 |
|||
4 |
|
0,0589 |
|
0,1189 |
|
0,1810 |
|
0,2450 |
|
0,3090 |
|
0,3678 |
|
0,4119 |
|
0,4283 |
|||
5 |
|
0,0720 |
|
0,1462 |
|
0,2248 |
|
0,3090 |
|
0,3983 |
|
0,4876 |
|
0,5616 |
|
0,5897 |
|||
6 |
|
0,0828 |
|
0,1692 |
|
0,2629 |
|
0,3678 |
|
0,4876 |
|
0,6225 |
|
0,7574 |
|
0,8072 |
|||
7 |
|
0,0901 |
|
0,1849 |
|
0,2899 |
|
0,4119 |
|
0,5616 |
|
0,7574 |
|
1,0384 |
|
1,1241 |
|||
8 |
|
0,0927 |
|
0,1906 |
|
0,2996 |
|
0,4283 |
|
0,5897 |
|
0,8072 |
|
1,1241 |
|
1,2217 |
|||
9 |
|
0,0901 |
|
0,1849 |
|
0,2899 |
|
0,4119 |
|
0,5616 |
|
0,7574 |
|
1,0384 |
|
1,1241 |
|||
10 |
|
0,0828 |
|
0,1692 |
|
0,2629 |
|
0,3678 |
|
0,4876 |
|
0,6225 |
|
0,7574 |
|
0,8072 |
|||
11 |
|
0,0720 |
|
0,1462 |
|
0,2248 |
|
0,3090 |
|
0,3983 |
|
0,4876 |
|
0,5616 |
|
0,5897 |
|||
12 |
|
0,0589 |
|
0,1189 |
|
0,1810 |
|
0,2450 |
|
0,3090 |
|
0,3678 |
|
0,4119 |
|
0,4283 |
|||
13 |
|
0,0446 |
|
0,0896 |
|
0,1353 |
|
0,1810 |
|
0,2248 |
|
0,2629 |
|
0,2899 |
|
0,2996 |
|||
14 |
|
0,0298 |
|
0,0597 |
|
0,0896 |
|
0,1189 |
|
0,1462 |
|
0,1692 |
|
0,1849 |
|
0,1906 |
|||
15 |
|
0,0149 |
|
0,0298 |
|
0,0446 |
|
0,0589 |
|
0,0720 |
|
0,0828 |
|
0,0901 |
|
0,0927 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 5 . 6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||
|
9 |
|
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
0,0901 |
|
0,0828 |
|
0,0720 |
|
0,0589 |
|
0,0446 |
|
0,0298 |
|
0,0149 |
|||||
2 |
|
0,1849 |
|
0,1692 |
|
0,1462 |
|
0,1189 |
|
0,0896 |
|
0,0597 |
|
0,0298 |
|||||
3 |
|
0,2899 |
|
0,2629 |
|
0,2248 |
|
0,1810 |
|
0,1353 |
|
0,0896 |
|
0,0446 |
|||||
4 |
|
0,4119 |
|
0,3678 |
|
0,3090 |
|
0,2450 |
|
0,1810 |
|
0,1189 |
|
0,0589 |
|||||
5 |
|
0,5616 |
|
0,4876 |
|
0,3983 |
|
0,3090 |
|
0,2248 |
|
0,1462 |
|
0,0720 |
|||||
6 |
|
0,7574 |
|
0,6225 |
|
0,4876 |
|
0,3678 |
|
0,2629 |
|
0,1692 |
|
0,0828 |
|||||
7 |
|
1,0384 |
|
0,7574 |
|
0,5616 |
|
0,4119 |
|
0,2899 |
|
0,1849 |
|
0,0901 |
|||||
8 |
|
1,1241 |
|
0,8072 |
|
0,5897 |
|
0,4283 |
|
0,2996 |
|
0,1906 |
|
0,0927 |
|||||
9 |
|
1,0384 |
|
0,7574 |
|
0,5616 |
|
0,4119 |
|
0,2899 |
|
0,1849 |
|
0,0901 |
|||||
10 |
0,7574 |
|
0,6225 |
|
0,4876 |
|
0,3678 |
|
0,2629 |
|
0,1692 |
|
0,0828 |
||||||
11 |
0,5616 |
|
0,4876 |
|
0,3983 |
|
0,3080 |
|
0,2248 |
|
0,1462 |
|
0,072 |
||||||
12 |
0,4119 |
|
0,3678 |
|
0,3090 |
|
0,2450 |
|
0,1810 |
|
0,1189 |
|
0,0589 |
||||||
13 |
0,2899 |
|
0,2629 |
|
0,2248 |
|
0,1810 |
|
0,1353 |
|
0,0896 |
|
0,0446 |
||||||
14 |
0,1849 |
|
0,1692 |
|
0,1462 |
|
0,1189 |
|
0,0896 |
|
0,0597 |
|
0,0298 |
||||||
15 |
0,0901 |
|
0,0828 |
|
0,0720 |
|
0,0589 |
|
0,0446 |
|
0,0298 |
|
0,0149 |
||||||
127
Простейшим итерационным методом решения систем алгебраических уравнений, аппроксимирующих краевые задачи, является метод Якоби [25]. Для двумерного уравнения (5.29) итерационный процесс записывается в виде
|
+ Ki−0,5, j + Ki, j+0,5 + Ki, j−0,5 |
+ q |
|
|
|
= Ki+0,5, j |
Ut |
+ |
|||||||||||||
Ki+0,5, j |
Ut+1 |
||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
i, j |
i, j |
|
|
2 |
|
i+1, j |
|
||||
|
hx |
|
|
|
|
hy |
|
|
|
|
|
|
|
|
|
hx |
|
|
(5.31) |
||
|
+ Ki−0,5, j |
|
|
|
+ Ki, j+0,5 |
|
|
+ Ki, j−0,5 Ut |
|
|
|
||||||||||
|
Ut |
Ut |
− f |
|
, |
|
|||||||||||||||
|
|
|
2 |
|
i−1, j |
|
2 |
i, j+1 |
|
|
2 |
|
|
i, j−1 |
|
i, j |
|
|
|||
|
|
|
h |
|
|
|
|
h |
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
|
|
|
где t |
– номер итерации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Этовыражение можно формально записатьследующим образом: |
|||||||||||||||||
|
|
U t +1 |
−U t |
|
2 |
|
|
|
t |
|
|
|
|
|
||||
|
|
|
i, j |
i, j |
|
∑ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
∆α U |
− |
f |
i , j |
, |
|
(5.32) |
|||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
τ |
|
|
|
|
i , j |
|
|
|
|
||||
|
|
|
|
|
|
α= 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
+ Ki−0,5, j |
|
|
Ki, j +0,5 |
+ Ki, j −0,5 |
−1 |
|
||||||||||
где |
τ = |
Ki+0,5, j |
+ |
|
. |
(5.33) |
||||||||||||
|
|
|
|
|
|
|
|
hy2 |
|
|
||||||||
|
|
hx2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Большинство итерационных методов можно символически за- |
|||||||||||||||||
писывать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
U t +1 −U t |
|
|
t |
|
|
|
|
|
|
||||||
|
|
|
Bt |
|
|
|
|
+ |
|
AU |
|
= − f , |
|
|
(5.34) |
|||
|
|
|
|
τ |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Bt − произвольно выбранный оператор.
Отсюда следует, что итерационный процесс можно рассматривать как разностную схему, соответствующую нестационарной задаче. Следовательно, для его реализации могут быть использованы рассмотренные ранее методы решения нестационарных краевых задач. В качестве оператора B можно использовать любой оператор, позволяющий быстро находить значения искомой функции Ut и обеспечивающий быстрое затухание начальных данных. К таким операторам можно отнести операторы, используемые при решении
128
нестационарных задач продольно-поперечным и локально-одномер- ным методами.
В отличие от нестационарных краевых задач продольно-попе- речные и локально-одномерные схемы реализуются таким образом, чтобы необходимая точность решения достигалась за минимально возможное время. В качестве примера рассмотрим решение стационарной краевой задачи с использованием продольно-поперечной схемы.
Пусть решается рассмотренная в примере 5.2 стационарная краевая задача.
Аппроксимируя дифференциальные операторы конечно-разност- ными выражениями, запишем дифференциальноеуравнение в виде
ut +1 |
− 2ut +1 |
+ ut +1 |
ut +1 |
− 2ut +1 |
+ ut +1 |
|
||
i +1, j |
i, j |
i −1, j |
+ |
i, j +1 |
i, j |
i, j −1 |
= f i, j . |
(5.35) |
|
h2x |
|
|
h2x |
|
|||
|
|
|
|
|
|
|
||
Для решения задачи итерационным методом представим записанное уравнение как уравнение нестационарной задачи (5.32):
U t +1 |
−U t |
ut +1 |
− 2ut +1 |
+ ut +1 |
ut |
− 2ut |
+ ut |
|
|
|||
i, j |
i, j |
= |
i+1, j |
i, j |
i−1, j |
+ |
i, j+1 |
i, j |
i, j−1 |
− f |
|
. (5.36) |
|
|
|
h2 |
|
|
h2 |
|
i, j |
||||
∆ t |
|
|
|
|
|
|
|
|||||
Полученное уравнение решается методом переменных направлений с учётом заданных граничных условий и принимаемых нулевыми начальных условий. Величина временного интервала для неявной схемы выбирается максимальной, обеспечивающей достижение необходимой точности за минимальное число итераций (∆ t= 0,1 против 0,001 при решении нестационарной задачи в при-
мере 3.4).
Результаты итерационного процесса представлены в табл. 5.7, где приведены значения искомой функции в центре исследуемой области, а также на рис. 5.4, где показана зависимость искомого решения в одной из точек исследуемой области U (N ) от числа
итераций N . Как видно из таблицы, для достижения необходимой
129
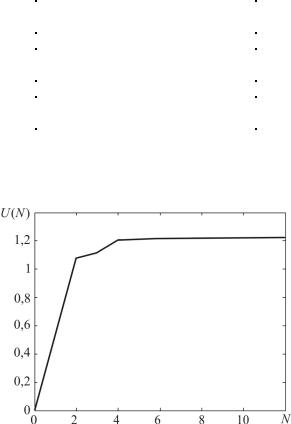
точности (см. примеры 5.1, 5.2) потребовалось 18 итераций, хотя уже при 5 итерациях относительная величина погрешности не превышает 0,5 %, при 10 итерациях − 0,05 %.
Таблица 5 . 7
Результаты итерационного процесса для решения краевой задачи
Номер |
Величина |
Номер |
Величина |
итерации |
функции |
итерации |
функции |
1 |
1,1484 |
12 |
1,2214 |
2 |
1,2015 |
13 |
1,2215 |
3 |
1,2063 |
14 |
1,2216 |
4 |
1,2136 |
15 |
1,2216 |
5 |
1,2164 |
16 |
1,2216 |
6 |
1,2184 |
17 |
1,2217 |
7 |
1,2195 |
18 |
1,2217 |
8 |
1,2203 |
19 |
1,2217 |
9 |
1,2208 |
20 |
1,2217 |
10 |
1,2211 |
21 |
1,2217 |
11 |
1,2213 |
|
|
Рис. 5.4. Характер протекания итерационного процесса при решении краевой задачи
130
