
1329
.pdf
ние распределения магнитного поля ЭМ вдоль её оси, затухающего при удалении от магнитопровода. На некотором расстоянии (теоретически равном бесконечности) от магнитпровода магнитное поле машины можно считать затухшим. Говорят, что в этом случае носителем финитной функции является вся числовая ось. В реальных условиях магнитное поле можно считать затухшим на расстоянии, равном величине десяти воздушных зазоров. Поэтому носителем будет являться интервал конечной величины.
При решении краевых задач, связанных с расчётами магнитного поля, широкое распространение получили следующие функции.
Единичная функция Хевисайда, которая определяется следую-
щим образом (рис. 1.1):
0 при |
x < 0, |
|
|||
|
1 |
|
|
|
|
|
|
|
|
||
E(x) = |
|
при |
x = 0, |
(1.3) |
|
2 |
|||||
|
|
|
|
||
1 при x > 0. |
|
||||
|
|
|
|
|
|
Единичная функция может быть записана для любой точки цифровой оси:
0 |
при x < x0 , |
|
|
|
|
|
|
E ( x − x0 ) = |
1 |
при x = x0 , |
(1.4) |
|
|||
2 |
|
|
|
1 |
при x > x0 . |
|
|
|
|
|
|
Рис. 1.1. Единичная функция Хевисайда
Единичные функции Хевисайда удобны для описания кусочнонепрерывных функций пространственных координат. Примером использования единичных функций является математическое выражение
11

для электропроводности проводника ограниченной длины в функции пространственной координаты (рис. 1.2). Математическая запись этой функции выглядит следующим образом:
γ(x) = γ[E(x − x1 ) − E(x − x2 ] . |
(1.5) |
При x < x1 γ(x) = 0; при x1 < x < x2 γ(x) = γ− 0 = γ; при |
x > x2 |
γ(x) = γ− γ = 0 . |
|
Рис. 1.2. Графическоеизображениеэлектропроводности вфункциипространственнойкоординаты
Единичная функция Хевисайда может быть аппроксимирована с определённой точностью непрерывными математическими функциями, например:
|
|
E(x) = |
1 |
+ |
1 |
arctg(mx) |
при m→∞ . |
(1.6) |
|
|
|
|
|
||||||
|
|
2 |
|
π |
|
|
|
||
Если x → −∞ |
, то arctg(mx) → − π |
2 . В этом случае E(x) → |
0 . |
||||||
Если |
x = 0 , |
то arctg(mx) = 0 и |
E(x) =1 2 . Если x → ∞ |
, то |
|||||
arctg(mx) → |
π 2 и E(x) → 1 . Графикфункции(1.6) показаннарис. 1.3. |
||||||||
Дельта-функция Дирака может быть представлена выражениями: |
|||||||||
∞ |
при x= |
0, |
δ(x) = |
при x ≠ |
(1.7) |
0 |
0. |
∞∫ δ(x)dx =1 .
−∞
Дельта-функция обладает фильтрующим свойством:
12
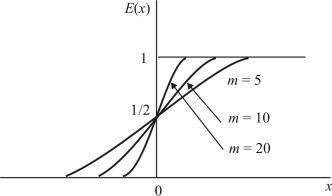
Рис. 1.3. Аппроксимация единичной функции выражением (1.6)
|
∞ |
|
|
|
∫ F (x)δ(x)dx = F (0) . |
(1.8) |
|
|
−∞ |
|
|
Так как δ(x) = 0 при x ≠ 0 произведение δ(x) F (x) равно нулю |
|||
всюду за исключением интервала −ε≤ |
x≤ ε при ε → 0 . В указанном |
||
интервале можно считать F (x) ≈ F (0) |
и потому функция может быть |
||
вынесена из-под знака интеграла: |
|
|
|
∞ |
ε |
ε |
|
∫ F (x)δ(x)dx = |
∫ F (0)δ(x)dx = F (0) ∫ δ(x)dx = F (0) . |
(1.9) |
|
−∞ |
−ε |
−ε |
|
|
|
|
|
Дельта-функция может быть записана для любой точки цифро- |
|||
вой оси: |
|
|
|
|
∞∫ F (x − x0 )dx = F (x0 ) . |
(1.10) |
|
|
−∞ |
|
|
С помощью дельта-функции удобно описывать плотность со- |
|||
средоточенных в точке величин. Если, например, к точке x0 |
прило- |
||
жена сосредоточенная сила величиной P , а в других точках число-
13

вой оси сила отсутствует, то плотность силы в функции пространственной координаты q(x) может быть записана в виде
q(x) = P δ( x − x0 ) . |
(1.11) |
При расчётах магнитных полей часто используется величина AS, называемая линейной плотностью тока. Под этой величиной обычно подразумевают суммарный ток, сосредоточенный в узком слое на поверхности магнитопровода с координатой z0 . Линейную плотность токав этом случае можно записатьследующим образом:
AS (z) = AS δ(z − z0 ) . |
(1.12) |
Дельта-функция может быть аппроксимирована различными аналитическими функциями, например:
δ(x) = |
m |
|
1 |
|
|
|
при m → ∞ . |
(1.13) |
|
|
|
|
|
||||||
|
π 1 + (mx)2 |
|
|
|
|
|
|||
Если x ≠ 0 , то δ(x) → |
0 . Если, наоборот, x = 0 , то |
|
|||||||
|
|
|
|
|
m |
|
|||
|
|
|
δ(x) → |
π= |
∞ . |
|
|||
Дельта-функция связана с единичной функцией Хевисайда сле- |
|||||||||
дующей зависимостью: |
|
|
|
|
|
|
|
|
|
|
|
|
δ(x) = |
dE(x) |
|
(1.14) |
|||
|
|
|
|
||||||
|
|
|
|
|
|
dx |
|
||
и, наоборот, |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
E(x) = ∫ |
δ(x)dx . |
(1.15) |
|||||
−∞
Действительно, в точке разрыва производная функции обращается в бесконечность, т.е. возникает импульсная функция (рис. 1.4).
14

Рис. 1.4. Единичная функция и δ -функция Дирака
Дельта-функция может не только интегрироваться, но и дифференцироваться бесконечно большое число раз. Производные дельта-функций также представляют комбинацию импульсных функций. Если представить дельта-функцию в виде треугольника, высота которого стремится к бесконечности, а основание – к нулю (рис. 1.5), то производная дельта-функции будет изображаться в виде комбинации прямоугольников различной полярности.
Рис. 1.5. Дельта-функция Дирака и её производная
15

Производная дельта-функции имеет определённый физический смысл. Если дельта-функция описывает плотность сосредоточенного в точке тока, то её производная описывает плотность диполя – системы двух зарядов, удалённых друг от друга на бесконечно малое расстояние [15].
В электротехнике дельта-функция может быть использована для описания многих электрических величин. Известно, что объёмная плотностьэлектрических зарядов записывается в виде [16]
ρ = |
lim |
∆ q |
при ∆ V→ 0 . |
(1.16) |
|
∆ V |
|||||
|
|
|
|
||
При стремлении ∆ |
V к нулю плотность ρ |
стремится к беско- |
|||
нечности. Поэтому приходится особо оговаривать, что ∆ V имеет конечные размеры, значительно меньшие, чем возможные расстояния между отдельными зарядами. Между тем объёмная плотность электрических зарядов может быть математически строго описана следующим выражением:
ρ = ∆ q δ( −x x0 )δ( −y y0 )δ(−z z0 ) , |
(1.17) |
где x0 , y0 , z0 – координаты точки расположения электрического
заряда.
Точно так же можно описать и поверхностную плотность зарядов − плотность электрического заряда, распределённого в поверхностном слое, толщина которого стремится к нулю:
σ= lim ∆ q при ∆ S→ 0 . (1.18)
∆S
Втерминах обобщенных функций поверхностная плотность записывается как
σ = ∆ q δ( x− x0 )δ( y− y0 ) . |
(1.19) |
Вместе стем необходимо отметить, чтодействие над самой дельтафункцией не является корректной математической операцией, посколь-
16

ку её значение в данной точке равно бесконечности, т.е. не определено. Для выполнения математических операций с дельта-функциями необходим переход от бесконечно больших величин к конечным. Этот переход осуществляется путём распределения дельта-функции на конечный интервал пространственной координаты:
δ( x) ≈ |
1 |
ε |
|
|
∫ δ(x)dx . |
(1.20) |
|||
2ε |
||||
|
−ε |
|
1.2. КВАНТОВАНИЕ ФУНКЦИЙ
При математическом моделировании ЭМ приходится решать сложные системы дифференциальных уравнений. Аналитические решения таких систем представляются возможными лишь в исключительных случаях, а для нелинейных уравнений практически невозможны. Поэтому основными методами решения указанных уравнений в настоящее время являются численные, предполагающие замену аналитических функций числовыми полями, над которыми производятся необходимые математические операции. В связи с этим термин «математическое моделирование» является адекватным термину «численное моделирование» или «численный эксперимент».
Таким образом, для реализации математической модели необходим переход от непрерывных аналитических функций к числовым полям. Переход от непрерывных функций к последовательностям дискретных значений величин обозначим как квантование функций.
Спроцессом квантования различных величин человек знаком
сдревнейших времён. Различного рода измерения представляют не что иное, как квантование этих величин. Именно операции с дискретными величинами явились основой математики. С развитием мысли в математике широкое распространение получил термин «функция», и последовательности дискретных значений стали рассматриваться в виде непрерывных последовательностей.
Новое рождение «кванта» появилось в работах М. Планка, когда использование непрерывных функций не позволило решить задачу
17

об излучении «чёрного» тела. С тех пор термин «квант» широко вошёл в обиход. Возникли новые понятия и термины: «квантовая механика» в механике, «квантовая биология» – генетика в биологии. С этих позиций современные численные методы, широко используемые для решения самых различных задач математики, с полным правом можно обозначить как «квантовая математика».
Для различного рода сигналов известны и широко используются на практике следующие виды квантования функций [13, 18]:
–квантование по координате;
–квантование по уровню сигнала;
–квантование по частоте спектра.
Наиболее распространённым видом квантования, применяемым в теоретических исследованиях и практике, является квантование по временной или пространственной координате. При этом виде квантования пространственная или временная координата делится на ряд интервалов и в каждом из них производится измерение исследуемой функции. Таким образом, непрерывная функция заменяется последовательностью одиночных импульсов, величины которых равны значениям исследуемой функции на данном интервале пространственной или временной координаты (рис. 1.6). Указанный вид квантования лежит в основе всех конечно-разностных методов.
Рис. 1.6. Квантование по координате
18

При квантовании функции по уровню её величина сравнивается с «квантом» функции. Ширина получаемых при этом отрезков характеризует градиент функции в зависимости от временной или пространственной координаты (рис. 1.7). В этом случае непрерывная функция пространственной или временной координаты представляет последовательность прямоугольных импульсов одинаковой амплитуды и различной длительности.
Рис. 1.7. Квантование по уровню
Третий вид квантования – по частоте спектра определяется возможностью разложения периодических или финитных непрерывных функций в ряд Фурье [18, 19, 23]. Разложение в указанный ряд предполагает нахождение коэффициентов разложения, т.е. нахождение амплитуды отдельных гармоник, составляющих ряд Фурье. Таким образом, искомая функция может быть представлена в виде последо-
19
вательности гармоник заданных частот с определёнными амплитудами. Для восстановления таких функций достаточно знание амплитуд гармоник в заданном интервале частот.
Для квантования математических функций в настоящее время наиболее часто используется квантование по координате и частоте спектра. Первый из этих способов лежит в основе конечно-разностных методов решений уравнений, третий используется для решения уравнений в частных производных методом разделения переменных.
Что касается второго способа квантования – квантования по уровню, то этот способ для решения уравнений практически не применяется, так как не разработан математический аппарат для систем алгебраических уравнений, получаемых при аппроксимации дифференциальных уравнений. Хотя в ряде случаев, при квантовании функций с малыми градиентами этот способ мог оказаться весьма эффективным.
В основе математических способов квантования лежит возможность представления непрерывных функций в виде разложения по системе базовых функций (СБФ) [18, 23, 27].
Для финитных непрерывных на интервале [а,b] функций справедливо разложение
∞ |
( x) , a ≤ x≤ b , |
|
f ( x) = ∑ck φk |
(1.21) |
k =0
где Ck – коэффициенты разложения; ϕ k – система базовых функций.
Для практических расчётов ряд усекают, ограничиваясь конечным количеством членов разложения.
Система базовых функций должна быть выбрана таким образом, чтобы на данном интервале обеспечивался минимум среднеквадратичной ошибки. Этому требованию отвечают системы ортогональных функций, которые чаще всего и используются для разложения функций.
Для ортогональных систем базовых функций справедливо соотношение
20
