1329

Рассматриваемая задача может быть решена с использованием локально-одномерного метода. Однако в этом случае для достижения необходимой точности приходится уменьшать величину временного интервала и увеличивать число итераций, так как простейшие схемы метода обладают первым порядком точности.

6. ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ

Конечно-разностные методы предполагают замену дифференциального уравнения системой алгебраических путём аппроксимации дифференциальных операторов конечно-разностными выражениями. Однако такой подход не является единственно возможным. Альтернативный способ получения системы алгебраических уравнений – представление решения краевой задачи в виде разложения по системе базовых функций, удовлетворяющих заданным граничным условиям.

Аналогичный случай рассматривался ранее при решении уравнения Пуассона методом разделения переменных. Однако в отличие от этого метода собственные значения и собственные функции дифференциального оператора в общем случае неизвестны. Поэтому коэффициенты разложения не могут быть рассчитаны с использованием простейших выражений. Их определение связано с решением системы алгебраических уравнений, получаемой для различных методов из определённых условий.

Показано [32, 33, 34], что решение краевой задачи с заданными граничными условиями эквивалентно поиску минимума функционала определённого вида. Эти вопросы рассматриваются разделом математики, называемым вариационным исчислением. Напомним, что функционалом называется объект математики, когда каждой из множества функций, принадлежащих этому объекту, может быть поставлено в соответствие определённое число.

131

Для решения задач вариационного исчисления, в частности нахождения минимума функционала, наиболее часто используются приближённые методы, к которым относятся методы Ритца и Бубнова– Галёркина. Эти методы так же, как и конечно-разностные, приводят к системе алгебраических уравнений, решаемых известными методами. Однако в отличие от последних методов система уравнений находится из условия:

−минимума функционала, если используется метод Ритца;

−ортогональности невязки уравнения к базовым функциям разложения, если используется метод Галёркина.

Метод Ритца применим для решения краевых задач с самосопряжёнными и положительно определёнными операторами дифференциальных уравнений.

Напомним, что самосопряжённым уравнением называется дифференциальное уравнение, записываемое в виде

К самосопряжённому виду путём определённых преобразований может быть приведено любое линейное дифференциальное уравнение второго порядка [34]

Дифференциальное уравнение считается положительно определённым, когда все собственные значения дифференциального оператора уравнения положительны.

Идея метода Ритца сводится к следующему. Пусть функционал J (u) в области D с граничными условиями на контуре Г, ограничи-

вающем эту область,

записывается в виде

132

D

Как указывалось выше, решение краевой задачи соответствует поиску минимума этого функционала.

Будем считать, что решение u представляется в виде разложения по системе пробных функций различного вида, удовлетворяющих заданным граничным условиям. Чаще всего в качестве пробных функций используют степенные или тригонометрические ряды с неопределёнными коэффициентами:

Подставляя указанное разложение (6.5) в выражение функционала (6.4), выполняя дифференцирование, интегрирование и другие, соответствующие функционалу математические преобразования, получим выражение, представляющее определённую функцию коэффициентов разложения c1 , c2 , ..., cn :

Для нахождения минимума функционала необходимо приравнять производные полученного выражения по искомым коэффициентам нулю:

∂

=0 , k =1, 2, ..., n, (6.7)

∂ck

врезультате чего получаем относительно их систему алгебраических уравнений. Решение этой системы позволяет определить коэффициенты разложения и восстановить решение краевой задачи (6.5).

Вряде конкретных задач решение может быть упрощено, если пробные функции являются линейными относительно искомых коэффициентов разложения, вследствие чего уравнения системы (6.7) оказываются первой степени, и для получения необходимой точности число уравнений может быть относительно небольшим.

Вметоде Галёркина решение краевой задачи также ищется в ви-

де разложения (6.5), а система алгебраических уравнений определяется из условия ортогональности невязки уравнения краевой задачи.J

133

Если, например, уравнение краевой задачи с однородными граничными условиями записано в виде

решение краевой задачи представлено в виде разложения

Опять получаем систему алгебраических уравнений, позволяющую определить коэффициенты разложения сj и восстановить искомую функцию u(x, y) .

Недостатком рассмотренных «классических» способов решения краевых задач является сложность их реализации для получения необходимой точности. Поэтому в настоящее время эти методы совершенствуются с целью упрощения построения системы алгебраических уравнений. Основная идея совершенствования – использовать в качестве базовых функций функции с финитным (конечным) носителем, т.е. функции, отличные от нуля лишь в окрестности рассматриваемой точки. В этом случае число членов каждого уравнения системы алгебраических уравнений для коэффициентов разложения будет определяться числом точек, принадлежащих финитному

134

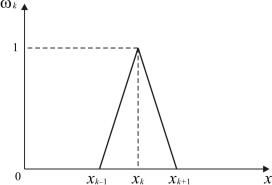
носителю базовой функции, а члены уравнения, соответствующие точкам за пределами носителя, будут равны нулю.

Примем для упрощения область определения решения краевой задачи 0 ≤ x≤ L одномерной. Разобьём указанную область 0 ≤ x≤ L на конечное число интервалов N и для каждого k-го интервала вве-

Эта функция отлична от нуля на интервале xk −1 ≤ x≤ xk +1 , состоит из двух линейных участков и достигает максимума, равного единице при x = xk (рис. 6.1).

Рис. 6.1. Базовая функция с финитным носителем

Подобно тому, как указывалось в п. 1.2, любую непрерывную кусочно-линейную финитную функцию можно представить в виде разложения по системе единичных базовых функций, причём в качестве единичных можно выбрать

135

где коэффициенты φk равны значениям функции φ(x) в точках xk .

Рассмотрим свойства базовой функции (6.12), определив её скалярное произведение:

Из выражения (6.14) следует, что функция ωk (x) ортогональна всем функциям ωn (x) , кроме ωk −1 , ωk , ωk +1 . Поэтому алгебраические уравнения, описывающие коэффициенты разложения φk , будут со-

держать всего три члена. Таким образом, использование базовых функций с финитными носителями позволяет значительно упростить структуру получаемой системы уравнений и применить для её решения рассмотренные ранее методы.

6.1. ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД РИТЦА

Методы Ритца, использующие функции с финитными носителями, принято обозначать как вариационно-разностные методы. Рассмотрим применение метода Ритца для решения одномерной краевой задачи, записываемой в виде

с однородными граничными условиями u(0) = 0, u(1) = 0 .

136

Решение краевой задачи соответствует поиску минимума функционала [33, 34]

Исследуемая область разбивается на N интервалов − конечных элементов, и решение краевой задачи ищется в виде разложения по системе базовых функций

В этом случае минимизируемый функционал может быть представлен суммой отдельных составляющих, записанных для каждого интервала разбиения пространственной координаты:

Запишем уравнение для одной составляющей функционала в точке xi на интервале xi −1 ≤ x≤ xi+1 . Искомое решение на этом интервале

137

Интеграл, входящий в выражение (6.19), может быть представлен в виде суммы двух интегралов для отдельных участков интервала

138

Условием минимума функционала является равенство нулю его производных по искомым величинам, в данном случае

Дифференцируя подынтегральное выражение по ui и группируя подобные члены, запишем уравнение (6.30) в виде

139

и используя известные граничные условия, получим систему трёхчленных алгебраических уравнений

тор с рассчитанными компонентами fi.

Решив указанную систему методом прогонки, определим значения коэффициентов ui, после чего рассчитывается искомое решение краевой задачи с использованием выражения (6.17).

140