Сопротивление материалов

ных долей единицы, следовательно, формулу можно переписать в более простом виде:

Приравнивая выражения (7.2) и (7.4), получим дифференциальное уравнение упругой балки (7.5):

Применяя аппарат определенного интегрирования, можно получить универсальные уравнения (7.8), (7.9) позволяющие найти параметры изогнутой оси балки при любых условиях закрепления ее концов, не прибегая к интегрированию дифференциального уравнения:

EJv = EJv0 + EJθ0 z ± ∑n Mi (z − ai )2 ± i=1 2!

114

нат, v0 , θ0 – прогиб и угол поворота в начале координат, называе-

мые начальными параметрами, а сам метод определения перемещений с помощью выражений (7.8), (7.9) называют методом начальных параметров. Начальные параметры определяют из условий закрепления балки. Так, для двухопорной балки (рис. 7.2):

а) v0 = 0 при z = 0 и v0 = 0 при z = l; б) v0 = 0 при z = a, v0 = 0 при

z = a + l; в) v0 = 0 при z = 0, θ0 = 0 при z = 0.

Для определения перемещений в ступенчатой балке можно использовать общие методы, изложенные в подразд. 7.4, 7.5, или применить видоизмененный метод начальных параметров, что вносит некоторые сложности.

Определение перемещений с помощью универсального уравнения должно включать следующие операции:

1.Определение реакций на опорах, анализ поперечных сил

иизгибающих моментов, подбор сечения балки.

2.Выбор начала координат, которое принято брать в левой крайней точке рассматриваемой балки.

3.Проведение произвольного сечения на последнем участке, считая от начала координат, расстояние до которого z. Если

115

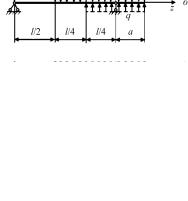
распределенная нагрузка обрывается на каком-либо участке (рис. 7.3, а), то ее продлевают до конца балки, а для восстановления действительных грузовых условий на продолжаемой длине прикладывают распределенную нагрузку обратного знака (рис. 7.3, б). Дополнительную и компенсирующую нагрузки принято показывать штриховыми линиями.

4. Запись уравнений для линейных (v) и угловых (θ) перемещений применительно к крайнему правому участку балки. Сосредоточенная сила и сосредоточенный момент, приложенные в крайнем сечении справа, в уравнения не входят.

5. Определение из условий закрепления начальных пара-

метров v0 и θ0 . Для того чтобы

вычислить перемещения какоголибо сечения, необходимо в соответствующие уравнения подставить координату z (только в те составляющие уравнений (7.8), (7.9), которые входят в промежуток между началом координат и рассматриваемым сечением).

7.2. Примеры расчета перемещений в балках методом начальных параметров

Пример

Для заданной балки (рис. 7.4, а) подобрать стандартный двутавр из условия прочности. Определить углы поворота и прогибы

в различных сечениях, построить эпюры θ и v; [σ] = 160 МПа,

E = 2 105 МПа, M = 40 кН м, F = 80 кН, q = 20 кН/м, l = 4 м, a = 1 м.

Решение

1. Определение реакций на опорах, анализ внутренних силовых факторов, подбор сечения.

116

Рис. 7.4.

117

Проверка: ∑Fy =0, RA +RВ −F −q l =10 +150 −80 −20 4 =0.

Анализ внутренних силовых факторов, подбор сечения:

Qy = RA −qz1, 0 ≤ z1 ≤ 4 м, Q(0) =10 кН, Q(4) = −70 кН.

z2

M x = RA z − q 21 , M (0) = 0, M (4) = −120 кН м,

Qy = F = 80 кН, M x = −F z2 , 0 ≤ z2 ≤1 м,

M (0) = 0, M (1) = −80 кН м.

Эпюры поперечных сил и изгибающих моментов представлены на рис. 7.4, в, г.

Из условия прочности по нормальным напряжениям подбираем сечение:

118

По ГОСТ 8239–89 ближайший номер двутавра № 40

сWx = 953 см3, Jx = 19062 см2.

2.Выбор начала координат в левом краевом сечении, запись универсальных уравнений для последнего участка (рис. 7.4, б).

4. Определение углов поворотов и перемещений в различных сечениях.

z = 0.

119

z = 4 м.

EJxθC =803 +40+5 52 +75−103 53 +103 =−146,7кН м2, θC =−3,8 10−3рад, z =5 м.

vА = vB = 0,

z = 2 м.

EJxvC = 803 5 + 20 + 53 53 + 25 − 56 54 + 56 = −108,3 кН м3 ,

vC = 2,8 10−3 м,

z =5 м.

По расчетным данным построены эпюры углов поворотов θ и перемещений v (рис. 7.4, д, е). Закономерности эпюр θ и v вытекают из дифференциальных зависимостей (7.7):

а) на участках, где M изг = 0, касательная к кривой θ = f(z) параллельна оси абсцисс. Там, где на эпюре моментов скачок, на эпюре θ наблюдается излом;

б) если на протяжении какого-либо участка изгибающий момент равен нулю, то эпюра θ прямоугольна, а эпюра v выражена прямой наклонной линией;

в) на участках, где изгибающий момент постоянный, эпюра θ– прямаянаклонная линия, эпюраv – парабола второго порядка;

120