Сопротивление материалов

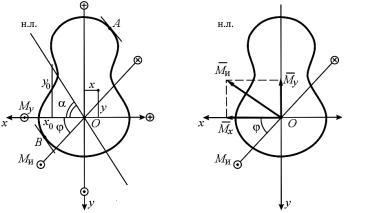
При действии внешних нагрузок в нескольких плоскостях возникает пространственный косой изгиб, в этом случае изогнутая ось стержня – пространственная кривая.

На рис. 9.2 действующие моменты Mx и My положительны. От этих составляющих моментов возникают нормальные напряжения, которые на основе принципа независимости действия сил для точки с координатами x и y определяются по формуле

где Mx и My – изгибающие моменты в рассматриваемом поперечном сечении; Jx и Jy – главные центральные моменты инерции сечения; x и y – координаты точки, в которой определяется напряжение (подставляются в формулу со своими знаками).

Мх

Рис. 9.2.

Таким образом, косой изгиб заменяется двумя плоскими изгибами в плоскостях xOz и yOz.

В поперечных сечениях стержня, кроме изгибающих моментов Mx и My, возникают и поперечные силы Qx и Qy. Но ввиду того, что при расчетах на прочность касательные напряжения весьма невелики по сравнению с нормальными напряжениями, их влиянием на прочность пренебрегают.

191

9.2. Распределение напряжений по сечению. Положение нейтральной линии. Условие прочности

Вычислив напряжения в ряде точек поперечного сечения, можно построить эпюру напряжений. Если полученные напряжения откладывать в виде отрезков из соответствующих точек перпендикулярно плоскости поперечного сечения, то концы всех отрезков расположатся на некоторой плоскости, уравнение которой выражается формулой (9.1). Эта плоскость представляет пространственную эпюру напряжений. Примерный вид плоскости напряжений показан на рис. 9.3

Рис. 9.3.

Если поперечное сечение стержня таково, что любая его центральная ось является главной (квадрат, круг, кольцо), то независимо от положения силовой плоскости изгиб будет прямым.

Рассмотрим произвольное сечение стержня, находящегося

вусловиях косого изгиба (см. рис. 9.2, б).

Всечении действует изгибающий момент Ми, не совпадающий ни с одной из главных осей инерции. Пусть линия действия изгибающего момента в сечении составляет с осью x

угол ϕ, положительное направление которого отсчитывается от оси абсцисс к оси ординат. В соответствии с принятым правилом указанный момент является положительным.

Разложим вектор момента Ми на составляющие:

M x = Mи sin ϕ и M y = Mи cos ϕ,

представив тем самым косой изгиб как сочетание двух плоских изгибов в главных плоскостях инерции стержня. Направление векторов суммарного момента и его составляющих устанавливаем по известному из теоретической механики «правилу буравчика».

192

Введем для составляющих моментов следующее правило знаков: момент считается положительным, если в первой четверти координатной плоскости (то есть при x > 0 и y > 0 ) он вызывает растягивающие напряжения.

Угловой коэффициент k1 следа плоскости момента представляет собой тангенс угла ϕ:

k1 = tg ϕ = M x .

M y

Для расчета на прочность необходимо определить положение опасного поперечного сечения по длине стержня и опасных точек в этом сечении. Положение опасного сечения определяется непосредственно по условию прочности. Для установления опасных точек в поперечном сечении необходимо знать положение нейтральной линии, поскольку нормальное напряжение пропорционально расстоянию от нее. Следовательно, наиболее удаленные от нейтральной линии точки и будут опасными.

Нейтральной линией, как известно, называется геометрическое место точек, где нормальные напряжения σ равны нулю. Подставляя условие σ = 0 в соотношение (9.1), получаем уравнение нейтральной линии

Здесь х0 и у0 – координаты произвольной точки нейтральной линии. Это уравнение представляет собой уравнение прямой, проходящей через начало координат (центр тяжести сечения) и не совпадающей ни с одной из главных осей, отсюда

Преобразуем выражение (9.3) к виду

193

Обозначая угол наклона нулевой линией к оси Ох через α (см. рис. 9.2, а), получим

Из формулы (9.4) следует, что при косом изгибе нейтральная линия не перпендикулярна к плоскости изгибающего момента.

Обозначим угловой коэффициент нейтральной линии:

k2 = tg α = −ctg ϕ J x . .

J y

Так как в общем случае J x ≠ J y , то условие перпендикулярности прямых не соблюдается, поскольку

k1 k2 ≠ −1.

При этом нейтральная линия отклоняется от вектора изгибающего момента Mи в сторону оси наименьшей жесткости

(tg α ≠ tg ϕ, α ≠ ϕ).

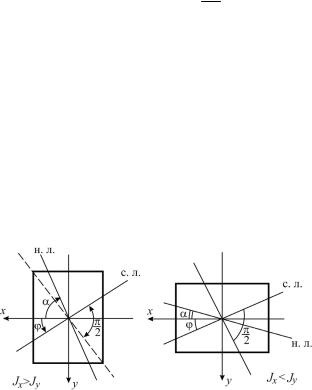
Иллюстрациейкданномувыводуявляетсярис. 9.4. Нарис. 9.4, а изображено сечение, у которого Jx > Jy. По формуле (9.4) получим, что tg α > tg ϕ, т.е. α > ϕ. Это значит, что нейтральная линия отклоняется от перпендикуляра к линии действия суммарного момента в сторону оси у.

194

На рис. 9.4, б показано сечение, для которого Jx < J y . При

этом tg α < tg ϕ, α < ϕ, следовательно, нейтральная линия отклоняется в сторону оси x.

Если Jx = Jy (сечение имеет более двух осей симметрии – квадратное, круглое, кольцевое и т.д.), то все центральные оси сечения являются главными, а значит, суммарный момент лежит всегда в одной из главных плоскостей. В этом случае изгиб является плоским.

После определения положения нейтральной линии к контуру сечения (при произвольном его очертании) проводятся касательные линии, параллельные нейтральной оси. Точки касания и определяют положение наиболее напряженных точек сечения (точки A и B на рис. 9.2, а).

Для стержня, изготовленного из пластичного материала, условие прочности будет иметь вид

где yоп и xоп – координаты опасных точек.

Для стержня из хрупкого материала составляются два условия прочности:

где [σ]p и [σ]сж – допускаемыенапряжениянарастяжениеисжатие.

Для сечений, имеющих две оси симметрии и точки, одновременно наиболее удаленные от обеих главных осей (прямоугольник, двутавр и подобные им), опасными являются те угловые точки, в которых напряжения от обоих изгибающих моментов имеют одинаковый знак.

195

Условие прочности в данном случае имеет вид

где Wx и Wy – осевые моменты сопротивления сечения.

Для подбора сечения балки при косом изгибе формулу (9.7) преобразуем к виду

Обозначим выражение, стоящее в скобках, через Mрасч:

это отношение обычно задается, что позволяет вычислить Wx, а затем размеры b и h. При подборе номера стандартного прокат-

ного профиля (двутавр, швеллер) учитывается, что отношение Wx

Wy

для всей совокупности профилей изменяется в довольно узких

пределах: для двутавров Wx = 7…12; для швеллеров – 3…10.

Wy

Из приведенных интервалов выбирается среднее отношение Wx

Wy

196

и по формуле (9.8) вычисляется Wx, затем по сортаменту для

соответствующего профиля берется уточненное отношение Wx

Wy

для выполнения следующего приближения. Процесс заканчивается, когда в результате последующей итерации расчет приводит к тому же номеру профиля.

Положениеопасного сечения определяется по условию (9.9).

9.3. Определение перемещений

Прогиб стержня при косом изгибе определяется на основании принципа суперпозиции как геометрическая сумма прогибов от независимого действия прямых поперечных изгибов в направлении главных осей инерции сечения. При этом искомый полный прогиб

f = u2 + v2 ,

где u и v – соответственно составляющие по осям х и у, вычисленные любым известным методом.

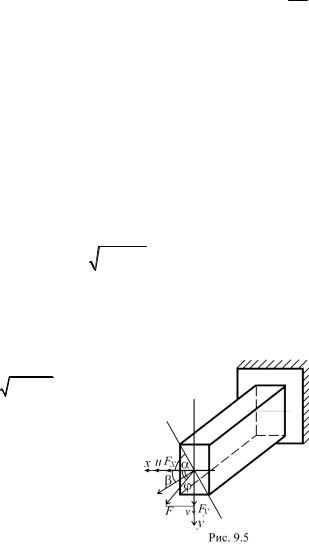
Например, перемещение концевого сечения консольной балки (рис. 9.5), нагруженной силой F,

щение концевого сечения консольной балки в направлении соответствующих осей х и у, определяе-

мые, например, по способу Вереща-

5. гина; Fх = F cos ϕ, Fy = F sin ϕ.

Покажем, что в каждом сечении балки полный прогиб перпендикулярен нейтральной линии:

197

Здесь β – угол наклона полного прогиба к оси x.

Произведение угловых коэффициентов полного прогиба и нейтральной оси будет равно

Пример

На двухопорную балку с консолью действует распределенная нагрузка q = 20 кН/м в вертикальной плоскости и сила F = 20 кН

в горизонтальной плоскости l = 4 м, а = 1 м, [σ] = 160 МПа,

Е = 2 105 МПа.

Подобрать сечение двутавра и прямоугольника с отношени-

ем сторон bh = 2 . Оценить отношение весов балок двутаврового

и прямоугольного сечения. Построить эпюру напряжений, найти положение нейтральной линии, определить перемещение сечения С для балки прямоугольного сечения.

Решение

1.Определение реакций на опорах от сил, действующих

ввертикальной и горизонтальной плоскостях.

∑МА = 0, RBг l − F (а+l )= 0, RBг = 204 5 = 25 кН;

198

Проверка:

RAв + RBв −q(l + a)= 0, 37,5 +62,5 −20 5 = 0,

RВг − F − RАг = 0, 25 −20 −5 = 0.

2. Анализ внутренних силовых факторов от сил, действующих в вертикальной и горизонтальной плоскостях, построение эпюр Q и М.

Вертикальная плоскость

199

Мy (0)= 0, Мy (4)= −5 4 = −20 кН м, 0 ≤ z2 ≤1 ì , Qx = F = 20 кН = сonst,

Мy = −Fz2 , Мy (0)= 0, Мy (1)= −20 кН м.

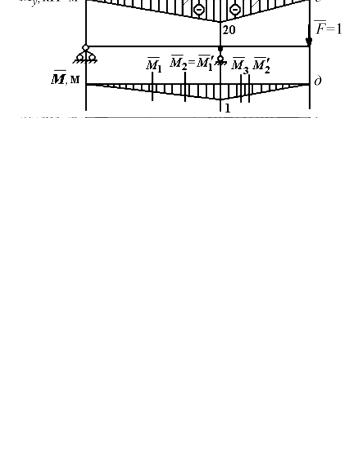
Строим эпюры поперечных сил и изгибающих моментов от сил, действующих в вертикальной плоскости (рис. 9.6, а, б) и от сил, действующих в горизонтальной плоскости (рис. 9.6, в, г).

Рис. 9.6.

200