1.Паутинообразная модель

1.1.Паутинообразная модель без учёта и с учётом запасов

Из общего курса микроэкономики известно, что колебания величин спроса и предложения как процесс постоянных изменений наглядно описывается паутинообразной моделью. Динамическая паутинообразная модель даёт представление о траектории перехода от одного состояния равновесия к другому и позволяет проанализировать закономерности установления рыночного равновесия с учётом фактора времени. При этом предполагается прямое движение товара от производителя к потребителю.

Вобщей паутинообразной модели термины «спрос», «предложение» и соответствующие им функции не определенны. В реальной действительности между продавцом и покупателем чаще всего есть посредник (торговля), изменения спроса и предложения могут быть как краткосрочными, так и долгосрочными, предложение не всегда означает объём производства. Если у производителя имеются запасы, то предложение товара будет больше объёма производства. В долгосрочном периоде рост объёмов производства может сопровождаться снижением издержек производства и, следовательно, снижением цены. В краткосрочном периоде цена будет ниже при покупке товаров оптом. Таким образом, с ростом цены предложение может как возрастать, так и падать.

Если, например, спрос увеличился в результате роста цен на товарызаменители, то величина предложения в заданный рыночный период остаётся неизменной, т.к. предполагается, что продавец не имеет запасов. В этом случае предложение равно объёму производства, а функция предложения описывает зависимость производства товара от цены на него. Объём производства и цена определяются одновременно через выравнивание спроса и предложения.

Внепрерывной модели цена превращается в функцию времени. Следовательно, величины спроса и предложения также оказываются функциями времени, условия равновесия на рынке преобразуются с учётом запаздывания во времени предложения по отношению к спросу. Если предположить, что рыночный спрос зависит от цен текущего периода (t), а предложение от цены предыдущего периода (t – 1), то имеется запаздывание в реакции производства на изменение цены.

Если мы исходим из линейной зависимости величин спроса и предложения от цены, т. е. цена является аргументом функции, то

5

При равновесии цена принимает такое значение, при котором производство не возрастает и не убывает. Паутинообразная модель иллюстрирует поиск равновесия на рынке данного товара при заданном значении цены p0 и показывает, что происходит с переменными модели, если t → . Если t → , то pt → p*, QD → Q*, St → Q*, то есть процесс, описываемый моделью, сводится к равновесным значениям цены и объёма. Равновесные значения переменных P, QD, QS соответственным обозначением P*, QD*, QS* .

В каждый данный момент времени спрос и предложение либо выше, либо

Обозначим r = , тогда (1.7) принимает следующий вид δt = (– 1)r δt–1.

Если выразить отклонение рыночной цены от её равновесного значения в любой момент времени через начальное отклонение, то δt = (–1)t rt δ0, т.к. pt = p* + δ, то в конечном виде получим уравнение pt = p* + (–1)z rt (p0 – p*).

Если r < 1 или c + a < 0, то при t → , pt → p*, с затухающими колебаниями, – равновесие устойчивое, если r = 1 или c + a = 0, то при t → , pt колеблется около её равновесного значения. И если r > 1 или c + a > 0, то при t → , pt отклоняется от своего равновесного значения на всё большую величину – равновесие неустойчивое, также неустойчиво равновесие при r = 1.

6

1.2. Паутинообразная модель с учётом запасов

Поиск равновесия будет другим, если у производителя есть запасы. В этом случае продажа товара может быть больше или меньше объёма производства за счёт изменения запасов. Прирост запаса Qt = Qt – Qt–1, где Qt – запас данного товара в момент времени t, следовательно, Qt = St – Dt. Отличие от случая без запасов состоит в следующем. Если запасов нет, то предложение определяет спрос,

апри наличии запасов спрос определяет предложение.

Вданной модели под термином «спрос» по-прежнему считаем объём реализации данного товара. Теперь допустим, что рыночная цена возрастает, если предложение товара в момент времени t пополняется за счёт запасов, и убывает в противном случае.

где λ – заданная положительная величина, характеризующая реакцию продавца товара на изменение запасов. Если функция спроса и предложения имеет вид:

Dt = apt + b,

St = cpt–1 + d,

то, подставив (1.5) и (1.6) уравнения в (1.8) и используя отклонение рыночной цены от равновесной (1.4), получим

δt = δt–1 – λ (сδt–1 – аδ),

отсюда

Так как a < 0, то 1 – λa > 0. Числитель этой дроби положителен, если λ < , и

отрицателен, если λ > . При любых значениях λ рассматриваемая дробь меньше

единицы. Отсюда 0 < λ < .

Равновесие устойчиво и рыночная цена монотонно приближается к её

-

равновесному значению, если 0 < < 1.

-

Равновесие устойчиво и рыночная цена приближается к её равновесному значению с затухающими колебаниями, если

7

Если с + а < 0 то (1.10) справедливо при λ > . Если с + а > 0, то (1.10)

выполняется при < λ < .

Мы знаем, что равновесие в паутинообразной модели без запасов устойчиво, если c + a < 0 и неустойчиво, если c + a > 0. Если совместить условия устойчивости и неустойчивости равновесия в модели без запасов и с запасами, то можно сделать выводы о том, что использование запасов позволяет преобразовать затухающие колебания в монотонные и монотонные колебания в затухающие, что позволит избежать нежелательных скачков рыночной цены. Таким образом, запасы, вопервых, смягчают рыночную конъюнктуру и, во-вторых, неустойчивое исходное (без запасов) равновесие может оказаться устойчивым.

Подставив цену pt (1.8) в функции спроса и предложения и используя формулу образования запасов Qt = Qt – 1 + St – Dt, находим величину запасов для случая монотонного приближения рыночной цены к равновесной цене.

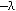
Qt = Q0 + (p0 – p*)[1 – )t].

Если p0 > p*, то происходит накопление запасов, в противном случае запасы сокращаются.

1.3.Паутинообразная модель Вальраса и Маршалла

Вмодели Вальраса рассматривается ожидаемый спрос в данный момент времени в зависимости от рыночной цены (pt). Предложение товара означает реакцию продавца на рыночную цену в данный момент времени.

Dt = apt + b, St = cpt + d, при этом с > 0, a < 0, т. е. спрос и предложение функции рыночной цены. Паутинообразная модель строится с учётом запасов

Qt = St – Dt.

Продавцы повышают цены пропорционально уменьшению запасов.

Подставим (1.12) и (1.13) в (1.11) и, используя отклонения рыночной цены от равновесной (1.4), получим равенство

δt = δt–1 – λ(сδt–1 – аδt–1) или δt = [1 – λ(с – а)] δt–1.

Если 0 < 1 – λ(с – а) < 1 или когда λ < - , равновесие устойчиво и рыночная

цена монотонно приближается к равновесной с затухающими колебаниями, когда 1 – λ(с – а) < – 1 равновесие неустойчиво.

Подставив цену Pt (1.11) в функцию спроса и предложения и, используя формулу образования запасов, находим формулу для случая монотонного

где q = [1 – λ(с – а)].

Если p0 > р* , то происходит накопление запасов, в противном случае запасы сокращаются. В модели Вальраса параметр λ может использоваться для регулирования размера запаса.

Другое толкование поиска равновесия дал А. Маршалл. Маршалл считал, что на рынке встречаются цена покупателя и цена продавца. Если цена покупателя выше цены продавца, то предложение товаров возрастает. Цену покупателя Маршалл выводил из функции спроса, а цену продавца – из функции предложения.

PDt = ; рSt = ,

где xt – предложение товара в данный момент времени.

Допустим предложение возрастает, если в предшествующий момент времени цена покупателя оказалась выше цены продавца:

Обозначим отклонение текущего предложения от равновесного через γt :

9

Подставим (1.16), (1.17) в (1.14) и, используя (1.15), приведём (1.14) к виду

γt = [1 – μ)] xt – 1.

Равновесие устойчиво и предпочтение товара монотонно приближается к его равновесному значению, если

0 < 1 – μ < 1 и когда 0 < μ < .

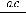Равновесие устойчиво и предложение товара приближается к его

Равновесие неустойчиво, когда μ > .

Для сопоставления моделей Вальраса и Маршалла найдём, при каких значениях λ и μ в любой заданный момент времени t предложение по Вальрасу полностью совпадает с предложением по Маршаллу.

Докажем, что при c > 0 предложение по Вальрасу полностью совпадет с предложением по Маршаллу, если μ = – асλ.

Для составления модели Вальраса и Маршалла найдём, при каких значениях λ и μ в любой заданный момент времени t предложение по Вальрасу полностью совпадет с предложением по Маршаллу, если μ = – асλ.

В модели Вальраса рыночная цена в момент времени t, выраженная через равновесное её значение, равна

С другой стороны, в модели Маршалла предложение в момент времени t, выраженное через равновесное его значение, равно

Поскольку S* = ср* + d = x*, то выбираем начальные условия так, чтобы они совпадали S0 = ср0 + d = x0. В этом случае формулу (1.19) можно записать так:

10

Из равенства St = xt следует: [1 – μ()]t = [1 – λ(с – а)]t.

Это равенство выполняется при μ = – асλ. Если c > 0, то для λ > 0 можно подобрать положительное μ такое, что динамика предложения по Маршаллу будет полностью совпадать с динамикой предложения по Вальрасу. Если же c < 0, то μ < 0, что противоречит предложению о поведении продавцов в модели Маршалла.

Итоги сравнения можно представить в таблице 1.

Таблица 1 – Сравнительная характеристика модели Вальраса и Маршала

Контрольные вопросы

1.Каким образом усложняется анализ стабильности равновесия в паутинообразной модели?

2.От чего зависит стабильность равновесия в паутинообразной модели?

3.В какой ситуации спрос и предложение приобретают паутинообразный вид?

4.Как влияют запасы на рыночную конъюнктуру в паутинообразной модели?

5. В чём заключается различие паутинообразных моделей Л. Вальраса и А. Маршалла.

11