4. Производственная функция и теория фирмы

4.1. Линия производственных возможностей

Производство есть процесс преобразования одних благ в другие: факторов производства в готовую продукцию. Одним их важнейших участников экономических процессов является производитель, который реализует свои цели только через потребителя, удовлетворяя его потребности.

Допустим, что имеется n различных товаров, количество n-го товара обозначается хn, тогда некоторый набор товаров обозначается Х = (x1, …, xn). Рассмотрим только неотрицательные количества товаров, так что Х > 0. Множество всех наборов товаров называется пространством товаров С. Набор товаров можно трактовать как корзину, в которой лежат эти товары в соответствующем количестве.

Пусть экономика работает в пространстве товаров С = {X = (x1, x2, …, xn)}. Пространство товаров состоит из неотрицательных n-мерных векторов. Рассмотрим теперь вектор T размерности n. Вектор X назовём вектором затрат, а вектор Y – вектором выпуска. Сам же вектор T = (X,Y) назовём вектором затрат-выпуска, или технологией. По своему смыслу технология (X,Y) есть способ переработки ресурсов в готовую продукцию: «смешав» ресурсы в количестве X, получим продукцию в размере Y. Каждый конкретный производитель характеризуется некоторым множеством τ технологий, которое называется производственным множеством. Типичное заштрихованное множество представлено на рисунок 4.1. Данный производитель затрачивает один товар для выпуска другого.

y

С

τВ

x

Рисунок 4.1 – Производственное множество

Производственное множество отражает широту возможностей производителя: чем оно больше, тем шире его возможности.

На рисунке 4.1 обозначены две точки В и С, которые соответствуют одинаковые затраты по этим технологиям и разный выпуск. Производитель не

52

выберет технологию В, раз есть более лучшая технология С. В данном случае, найдём для каждого x ≤ 0 самую высокую точку (x, y) в производственном множестве. Очевидно, при затратах х технология (x, y) самая лучшая. Никакая технология (x, b) при b < y не должна выбираться производителем по очевидным причинам. Итак, в данном случае (с двумя товарами) легко получить функцию y = f(x) для x ≤ 0; она называется производственной функцией.

Из рисунка 4.1 видно, что для всякого x ≤ 0 такая точка y = f(x) единственна, что, собственно, и позволяет говорить о производственной функции. Но так просто дело обстоит, если выпускается только один товар. В общем случае для вектора затрат Х обозначим множество Мх = {Y:(X,Y) τ}. Множество Мх – это множество всех возможных выпусков при затратах Х. В этом множестве рассмотрим кривую (линию) производственных возможностей Kx = {Y Мх}, Kx – это множество наилучших выпусков. Если выпускаются два товара, то это кривая, если же выпускается более двух товаров, то это поверхность, тело или множество еще большей размерности.

Для любого вектора затрат Х все наилучшие выпуски лежат на кривой (поверхности) производственных возможностей. Поэтому из экономических соображений оттуда и должен выбрать производитель технологию. Для случая выпуска двух товаров y1, y2 картина показана на рисунке 4.2.

y2

Кривая

производственных возможностей Kx

Mx

y1

Рисунок 4.2 – Кривая производственных возможностей

Кривая (линия) производственных возможностей графически иллюстрирует возможности одновременного производства двух продуктов с учетом ограниченности ресурсов, расходуемых на производство этих продуктов. Кривая строится в системе координат, каждая из которых отражает объем производства одного из продуктов. Она ограничивает область производственных возможностей, так что любая точка на кривой показывает предельно возможное по ресурсным ограничениям сочетание объёмов производства двух продуктов.

53

Рассмотрим следующий пример. Предприятие выпускает два продукта. Количество первого обозначим через X, а второго – через Y. Зависимость выпуска от затрат труда для каждого из продуктов:

Относительно производственных функций (4.1) – (4.2) предполагается, что их первые производные больше нуля, а вторые – меньше нуля. Смысл этих предположений следующий: предельная производительность труда, величина положительная, и она убывает с ростом затрат труда.

Допустим затраты труда являются однородными и общие затраты труда на производство обоих продуктов равны L, так что:

(4.3)

Используя производственные функции (4.1) – (4.2), выразим затраты труда как функции объёмов производства:

(4.4)

(4.5)

Подставив (4.1.4) и (4.1.5) в (4.1.3), получим:

(4.6)

Считая общие затраты труда постоянными (L=const), продифференцируем выражение (4.6) по X:

(4.7)

Из (4.7) получаем:

(4.8)

В равенстве (4.1.8) справа стоит отношение предельной трудоёмкости продукта Х к предельной трудоёмкости продукта Y. В левой части равенства стоит величина, которую называют предельной нормой преобразования. При предположениях, накладываемых на производственные функции,

(4.9)

Следовательно, линия (4.6) – выпукла вверх (риунок 4.2).

54

Движение вдоль линии производственных возможностей означает, что можно увеличить производство одного продукта только ценою сокращения производства другого.

Обозначим через pX и pY цены соответственно продукта X и Y. Допустим, предприятие максимизирует выручку pX×X+pY×Y. Тогда постановка следующей задачи: pX×X+pY×Y →max, при ограничении .

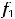
Геометрическая иллюстрация решения задачи представлена на рисунке 4.3.

Y

линия pX×X+pY×Y

0 X

Рисунок 4.3 – Задача максимизации выручки

Выручка максимальна в точке касания линии pX×X+pY×Y и линии производственных возможностей. В этой точке предельная норма преобразования равна отношению цен на продукты:

.

4.2. Производственная функция

Производственной функцией называется аналитическое соотношение, связывающее переменные величины затрат (факторов, ресурсов) с величиной выпуска продукции. Производственные функции предназначены для моделирования процесса производства некоторой хозяйственной единицы: отдельной фирмы, отрасли или всей экономики государства в целом. Общий вид производственной функции: Y = Y(X1, X2, …, Xi, …, Xn), где Y – показатель, характеризующий результаты производства; X – факторный показатель i-го производственного ресурса; n – количество факторных показателей.

Обозначим объём выпускаемой продукции через Х, затраты труда – через L и затраты капитала – через K. Производственная функция будет иметь вид:

55

Будем предполагать, что применяемый при изготовлении продукции труд однороден и однородны также отдельные единицы затрачиваемого капитала. Кроме этого, затраты труда и капитала бесконечно делимы. Точно такие же предположения будем использовать и относительно выпуска продукции.

Другие предположения относительно вводимой производственной функции состоят в следующем. Выпуск продукции предполагается максимальным при данных затратах. При увеличении одного вида затрат и при неизменном объеме затрат другого вида выпуск продукции увеличивается. Иначе говоря, частные производные функции больше нуля:

Эти частные производные называют предельной производительностью капитала и предельной производительностью труда соответственно. Запишем уравнение полного дифференциала для производственной функции (4.10):

(4.12)

Для линий постоянного выпуска dX = 0 (X = const) и, следовательно,

(4.13)

Из равенства (4.13) получаем:

В равенстве (4.14) слева стоит величина, которую называют предельной нормой замещения. В правой части равенства записано отношение честных производных. Вдоль линии постоянного выпуска предельная норма замещения равна отношению частных производных.

Предельная норма замещения показывает, на сколько должны снизиться (возрасти) затраты капитала при увеличении (сокращении) затрат труда и при условии, что объём производства не изменится. Таким образом, оценка одного производственного фактора (например, труда) выражается в единицах другого (капитала). Поэтому предельная норма замещения относится к фундаментальным понятиям современной экономической теории.

Зависимость прироста выпуска продукции от увеличения всех производственных факторов характеризуется отдачей от масштаба, которая в свою очередь может быть убывающей, постоянной и возрастающей. Для оценки отдачи от масштаба используют понятие однородности. Производственная функция

56

называется однородной, если при увеличении всех факторов производства в k раз объём выпуска увеличивается в kn раз. Здесь n – показатель степени однородности. Таким образом, производственная функция Q = Q (L,K) является однородной в степени n, если:

Если n = 1, то функция однородна в первой степени, а производство демонстрирует постоянную отдачу от масштаба. В этом случае говорят, что функция линейно-однородная.

Если n > 1, то имеет место возрастающая отдача от масштаба. Если n < 1 – убывающая отдача от масштаба.

Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи может служить расстояние вдоль луча, проведённого из начала координат, между изоквантами, представляющими кратные Q объёмы выпуска – Q, 2Q, 3Q (рисунок 4.4).

К

2Q

K a

Q

0 L L 2L 3L

Рисунок 4.4 – Отдача от масштаба при однородной производственной функции

В экономической теории часто используются однородные первой степени производственные функции, для которых изменение каждой из переменных в q раз приводит к изменению выпуска в q раз:

Для однородных первой степени производственных функций справедливо уравнение Эйлера:

(4.16)

Обозначим эластичность выпуска по капиталу через α и эластичность выпуска по труду, через β:

57

.

Для однородных первой степени производственных функций сумма эластичностей выпуска по капиталу и труду равна единице: α + β = 1.

При уменьшении доступности предложения факторов объём производства фирмы зависит от её способности осуществлять замену ресурсов. Степень заменяемости одного фактора на другой измеряется сопоставлением изменения величины MRTS с изменением соотношения (K / L). При этом возможны два крайних случая.

В первом крайнем случае ресурсы являются совершенными субститутами, и изокванты приобретают вид прямых линий: величина MRTS постоянна при изменении K / L (рисунок 4.5 а). Во втором крайнем случае факторы производства являются совершенными комплементами без возможности замены, а изокванты приобретают L-образную форму (рисунок 4.5 б).

Форма линий изоквант зависит от степени заменяемости одного фактора производства на другой. Степень заменяемости измеряется эластичностью замены (σ), которая показывает, на сколько процентов должна измениться капиталовооружённость труда, чтобы при изменении соотношения производительностей факторов на 1 % выпуск остался неизменны и определяется как отношение изменения величины K / L на соответствующее изменение величины

MRTS:

Эластичность замены всегда является положительной величиной, которая изменяется между нулём и бесконечностью. Например, если два фактора производства совершенно заменяемы, то MRTS является величиной постоянной, d(MRTS) = 0, а величина σ – бесконечно велика. В случае совершенных комплементов величина K / L постоянна; d(K / L) = 0, а величина σ = 0. Таким

58