Назаметдинов Анализ данных 2012

v´F´Fv = v′λv= λv´v = λmin .

Собственный вектор, отвечающий минимальному собственному значению λmin показывает, какие из столбцов матрицы F порождают мультиколлинеарность.

в. Мера обусловленности ( мера Неймана−Голдстейна).

Мера λmin несет на себе эффект выбора масштаба измерения

входных переменных. Мера обусловленности определяется как отношение максимального и минимального собственных чисел

матрицы F′F, т. е. λmax 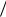λmin .

г. Максимальное значение парной сопряжённости (корреллированости) столбцов матрицы F. Матрица сопряжённости R,

определённая по матрице F, есть

где rij cos(Fi , Fj ) .

Напомним, что мы пользуемся термином сопряжённость, поскольку входные переменные неслучайны. Максимальный по модулю недиагональный элемент матрицы R

, i,j=0,1,…,k

может служить мерой мультиколлинеарности. Чем ближе введённая мера к единице, тем выше степень мультиколлинеарности. Максимальный коэффициент сопряжённости является безразмерным, не несёт на себе эффект масштаба. К сожалению, эта мера выражает только парную коллинеарность.

Три вектора на плоскости являются коллинеарными (компланарными по терминологии аналитической геометрии). Однако при этом они не обязательно сопряжённые. Например, комбинация из двух ортогональных векторов и третьим вектором, являющимся их биссектрисой, имеет матрицу сопряжённости

81

д. Максимальная множественная сопряжённость. Ищется регрессия каждой из базисных функций fi , i=1,…,k, на все остальные f0, f1,…,fi-1, fi+1,…,fk.. Для каждой регрессии подсчитывается

коэффициент детерминации Ri2 , i=0,1,…,k. В качестве меры муль-

Мера (4.8) не зависит от масштаба измерения входных переменных, хорошо интерпретируется. Она равна косинусу угла между вектором Fi, соответствующим базисной функции fi , и подпространством, натянутым на остальное множество базисных функций

F0,F1,…,Fi-1,Fi+1, Fk.

Наиболее информативными считаются меры λmin, λmax / λmin, max Ri . Именно они подсчитываются в первую очередь, когда имеется подозрение на мультиколлинеарность.

4.2.3. Методы борьбы с мультиколлинеарностью

Возможны три подхода к оцениванию коэффициентов регрессии при наличии мультиколлинеарности:

отсев базисных функций; переход к смещённым оценкам;

изменение информационной базы.

Отсев базисных функций может проходить по схеме прямого отсева либо косвенного с использованием процедур ортогонализации. При прямом отсеве проверяется гипотеза Hi: ai=0 (предполагается, что случайные возмущения нормальны). Если гипотеза Hi принимается, соответствующая базисная функция исключается и регрессия пересчитывается заново. Методы отсева сравнительно просты, однако их использование не бесспорно. Основная пробле-

82

ма здесь связана с относительной грубостью процедуры приравнивания нулю некоторых оценок. “Подозрительная” переменная, которая “сильно коррелирует“ c некоторыми другими – кандидат на исключение – часто имеет большой содержательный смысл. Исследователя вполне устроит более или менее удовлетворительная оценка коэффициента при этой переменной (базисной функции). В случае же отсева эта переменная выходит из анализа, так как оценка коэффициента при ней принимается нулевой.

Смещённые оценки. Как уже отмечалось, мультиколлинеарность ведет к возрастанию дисперсии оценок, а следовательно, сами оценки принимают очень большие значения. Легко показать, что с возрастанием мультиколлинеарности норма (длина) вектора оценок коэффициентов регрессии стремится к бесконечности. Действительно,

M[aˆ'aˆ] M[(a F F 1 F u) (a F F 1 F u)]

M[(a u F F F 1)(a F F 1 F u)]

M[(a a u F F 1 a a F F 1 F u u F F F 1 F F 1 F u]

a a σ2Sp F F 1 a a σ2 k 1 .

i0 i

Преобразование последнего из четырех слагаемых под знаком М проходило по схеме, рассмотренной в п. 3.3.3. Напомним также, что след матрицы равен сумме ее собственных значений, собственные значения обратной матрицы есть обратные величины от собственных значений прямой. При нарастании мультиколлинеарности min матрицы F′F стремится к нулю, так что M[aˆ'aˆ] . Задачу оценивания в условиях мультиколлинеарности можно сформулировать так: найти оценку параметров регрессии, которая была бы устойчивой и ее ошибка (дисперсия) не росла бы до бесконеч-

ности при усилении мультиколлинеарности.

~

Поиск оценок будем вести в классе линейных по y оценок как

наиболее простых. По теореме Гаусса−Маркова ковариационная матрица вектора МНК-оценок является “нижней границей” для всех линейных несмещенных оценок. Легко показать, что суммар-

83

ная дисперсия компонентов вектора оценок a стремится к бесконечности при возрастании мультиколлинеарности. Действительно,

Поскольку нижняя граница стремится к бесконечности, то и остальные линейные несмещенные оценки будут также расходиться (в смысле точности оценивания).

Оказывается, если отказаться от условия несмещенности, можно

~

построить линейные по y оценки a , для которых средний сум-

марный квадрат отклонения от истинных значений а будет меньше,

M[(a a)' (a a)] M[(a a)' (a a)] .

Решение здесь оказывается возможным при наложении ограничений на множество априорных значений а, обычно это требование, чтобы норма (длина) вектора а не превышала некоторой кон-

станты с, т. е. a c .

Наиболее известными в классе линейных смещенных оценок являются так называемые ридж-оценки. Ридж-оценка получается путем регуляризации дисперсионной матрицы. Ридж-оценка вектора коэффициентов регрессии в общем виде записывается так:

где K – некая неотрицательно определенная матрица.

Коррекция матрицы (F′F)-1 делает ее лучше определенной, а оценки – более устойчивыми. Обычно матрицу К выбирают диагональной, причем элементы этой матрицы берутся пропорциональными элементам главной диагонали матрицы (F′F), т.е.

kii μ (F' F)ii , kij 0 (i j), μ 0 . (4.9)

Еще более простой способ – к каждому диагональному элементу (F′F)ii добавляют одно и то же число μ 0 , т.е. K μI(k 1) . Путем линейных преобразований случай (4.9) можно свести к последнему.

84

т.е. действительно есть ридж-оценка, где матрица К является a

диагональной и скалярной ( K μI(k 1) ).

Верно и обратное, ридж-оценка имеет минимальную длину в

классе оценок с данным значением суммы квадратов отклонений

[4].

Интерес представляет средняя сумма квадратов (квадрат длины) ошибок ридж-оценок (4.10)

.

H (μ) M[(a(μ) a)'(a(μ) a)]

С ростом μ Н( ) сначала убывает, а затем начинает расти. В литературе приводится оценка μ* , доставляющая минимум H μ ,

однако непосредственно воспользоваться ею затруднительно. Простой практический прием поиска приемлемого μ следующий: строят ридж-оценку при разных μ и подсчитывают сумму квадратов отклонений, иначе остаточную сумму квадратов, SR . При наличии мультиколлинеарности рост SR на участке (0,μ*) незначительный, а

85

на (μ*, ) – большой. Точку излома μ* графика SR μ и берут в ка-

честве решения.

Изменение информационной базы в борьбе с мультиколли-

неарностью [5]. Пусть имеется возможность задавать входные данные по усмотрению исследователя, т.е. осуществить активный эксперимент. Возникает вопрос: как задать значения входных переменных, чтобы дополнительные данные способствовали снижению мультиколлинеарности, а следовательно, и ошибок оценивания? Для простоты изложения ограничимся линейной моделью без свободного члена, тогда матрица F совпадает с матрицей Х.

Как уже отмечалось, суммарная дисперсия оценок коэффициентов регрессии зависит от обратных собственных значений матрицы F′F , или в нашем случае, X′X. Выходит, наибольшее влияние на суммарную дисперсию оказывает наименьшее собственное значение. Если дополнительные данные увеличат min и не уменьшат

остальные собственные значения, то суммарная дисперсия заведомо уменьшится.

Предположим, что имеющаяся матрица Х дополнена строкой d ν min, где νmin– собственный вектор, отвечающий минимальному собственному значению λmin , d – некоторое отличное от нуля число. Расширенная матрица X * имеет вид

dv'min

Тогда

X* ' X* X ' X d 2vmin vmin ',

X* ' X*vmin X ' Xvmin d 2vmin vmin 'vmin (λ d 2 )vmin , (4.11)

поскольку vmin 'vmin 1.

Из (4.11) видно, vmin является собственным вектором матрицы X* ' X* , соответствующим собственному значению ( +d2). Легко показать, что остальные собственные векторы матрицы Х ′Х будут собственными векторами и матрицы X* ' X* . Действительно,

86

X '* X*vi X ' Xvi d 2vminv 'min vi λivi .

(В силу ортогональности собственных векторов v'min vi 0 .)

Таким образом, дополнив выборку Х наблюдением в точке d v 'min ,

действительно удалось увеличить наименьшее собственное значение матрицы Х′Х.

4.3. Качественные переменные в регрессии

Наряду с количественными переменными в правой части уравнения регрессии могут присутствовать и качественные переменные. Например, в исследовании зависимости уровня заработной платы в качестве таких переменных могут выступать: пол (мужской, женский), уровень образования (начальное, среднее, высшее). Можно было бы сгруппировать выборку, обеспечив в пределах подвыборки неизменность значений качественных переменных (подвыборка 1: мужчины с начальным уровнем образования, подвыборка 2: женщины с начальным уровнем образования, …, подвыборка 6: женщины с высшим образованием), а затем построить регрессии для каждой подвыборки. Подобный подход, хотя и возможен, не является эффективным, поскольку связан с потерей информации из-за уменьшения объема выборки. За счет введения бинарных, булевых, переменных оказывается возможным оценивать одно уравнение по всей выборке сразу. В литературе эти переменные часто называют фиктивными.

Как это делается, проиллюстрируем на примерах. При исследовании зависимости зарплаты от различных факторов пытаются выяснить, влияет ли на размер зарплаты и, если да, то в какой степени, наличие у работника высшего образования. Первоначальная модель (без учета уровня образования) имела вид

Теперь в модель необходимо включить такой качественный фактор, как наличие или отсутствие высшего образования. Введем но-

вую переменную z, полагая, что zi 1, если в i -м наблюдении ин-

87

дивидуум имеет высшее образование, и zi 0 , в противном случае. Уравнение регрессии теперь специфицируется в виде

где b – коэффициент регрессии при новой переменной z. Иными словами, ожидаемая зарплата для лиц без высшего образования составляет a f x , а при его наличии – a f x + b. Величину b мож-

но интерпретировать как среднее изменение зарплаты при переходе из одной категории (без высшего образования) в другую (с высшим образованием) при неизменности остальных факторов.

К уравнению (4.12) применяют МНК (при этом в матрице значений базисных функций появится дополнительный столбец, отвечающий переменной z) и получают оценки a и b. Тестируя гипотезу b=0, проверяют предположение о несущественном различии в зарплате между категориями.

Если качественная переменная имеет несколько (для определенности m) значений (уровней), то вводят m-1 бинарную переменную. Пусть, например, строится функция спроса на сезонный то-

та сезонности введем три бинарные переменные z1, z2 , z3 :

z1t =1, если месяц t является зимним, z1t =0 − в остальных случаях; z2t =1, если месяц t весенний, z2t =0 − в остальных случаях;

z3t =1, если месяц t является летним, z3t =0 − в остальных случаях. Уравнение регрессии ищется в виде

Обратим внимание на то, что четвертая бинарная переменная z4 , отвечающая осенним месяцам, вводиться не должна. Иначе для

любого t выполнялось бы соотношение z1t z2t z3t z4t 1 , т.е. сум-

ма последних четырех столбцов матрицы значений равнялось бы первому столбцу, отвечающему свободному члену. Это означало бы линейную зависимость и, как следствие, невозможность получить МНК оценку.

88