Назаметдинов Анализ данных 2012

Определенные сложности представляет проблема выбора постоянной сглаживания. В значительной мере этот выбор определяется целями исследования и конкретными свойствами ряда. Если сглаживание проводится с целью прогнозирования, то наилучшее значение α будет зависеть от горизонта, иначе срока, прогнозирования τ. Для краткосрочных (конъюнктурных) прогнозов более актуальной является свежая информация, тогда как при больших τ желательно ослабить влияние конъюнктурных колебаний и в большей мере учитывать прошлые данные, увеличивая тем самым период ретроспекции. Введем понятие возраста данных, считая, что текущее наблюдение имеет возраст, равный нулю, возраст предыдущего наблюдения равен единице и так далее. В качестве среднего значения tср возраста данных примем сумму возрастов с весами, использованными для подсчета сглаженной величины:

Чем меньше α, тем больше средний возраст данных. Подбор конкретного значения α обычно осуществляют экспериментально среди возможных значений перебором на сетке от 0,1 до 0,9 с шагом 0,1. Используемый критерий здесь – минимум суммы квадратов отклонений между наблюденными и прогнозными значениями ряда. Напомним, что в соответствии с моделью ряда (7.2) ожидаемое прогнозное значение ряда на момент t+τ есть сглаженное значение ряда на момент t, т.е. Myt aˆt .

Экспоненциальное сглаживание высоких порядков

Обобщим метод экспоненциального сглаживания на случай, когда модель процесса определяется линейной функцией a+bt [13]. Как и прежде, при заданном минимизируется

SR ( yt j a bj)2 β j . j 0

(Здесь для удобства представления знаки и опущены.)

151

вать как сглаживание 1-го порядка. По аналогии строят сглаживание 2-го порядка:

StII (1 β)(St βSt 1 β2St 2 ...)

(1 β)2 ( yt βyt 1 β2 yt 2 ...

βyt 1 β2 yt 2 ...

β2 yt 2 ...)

(1 β)2 yt j ( j 1)β j (1 β)2 ( yt j jβ j yt jβ j )

(1 β)2 yt j jβ j (1 β)St .

Система уравнений примет вид:

152

где ut yt (at 1 bt 1 1) – ошибка прогноза по линейной модели

на один такт вперед.

Рассмотренную выше процедуру можно обобщить на случай

полиномиальных трендов более высокого порядка (на практике не выше второго: y t = a 0 + a 1 t + a 2 t 2 ).

В описанных выше моделях содержался единственный параметр экспоненциального сглаживания β = 1 – α . Однопараметрические модели предложены Брауном. Кроме модели Брауна известно несколько вариантов многопараметрических адаптивных моделей. Так, для линейно изменяющегося процесса часто используется двухпараметрическая модель Хольта, в которой оценка коэффициентов производится следующим образом:

at α1 yt (1 α1)(at 1 bt 1); bt α2 (at at 1) (1 α2 )bt 1 ,

где α1 и α2 − параметры экспоненциального сглаживания, лежащие в диапазоне от 0 д о 1 . Адаптивность модели к новым данным наглядно видна, если ее переписать в виде:

153

at at 1 bt 1 α1ut ; bt bt 1 α1α2ut ,

где ut yt (at 1 bt 1 1) – ошибка прогноза на один такт вперед.

7.5. Анализ сезонной компоненты

Рассмотрим сначала процедуру оценивания сезонных эффектов. Пусть исходный ряд является полностью аддитивным, т.е.

y t = g t + s t + u t .

Необходимо оценить st по наблюденным yt. Иными словами, необходимо получить оценки cˆi коэффициентов cˆi , i 1,2,..., ин-

дикаторной модели.

Как уже отмечалось, сезонный эффект проявляется на фоне тренда, поэтому вначале необходимо оценить трендовую состав-

ляющую одним из рассмотренных методов. Затем для каждого сезона i, i=1,2,..,τ вычисляют все относящиеся к нему разности

значение тренда.

Каждая из этих разностей дает совместную оценку сезонного эффекта и случайной компоненты.

Производя усреднение полученных разностей, получают оценки эффектов. Полагая, что исходный ряд содержит целое число k периодов сезонности и ограничиваясь простым средним, имеем

С учетом условия репараметризации, требующим, чтобы сумма сезонных эффектов равнялась нулю, получаем скорректированные

оценки c i cˆi 1 cˆi .i 1

154

В случае мультипликативного сезонного эффекта, когда модель

На практике считается, что для оценки сезонных эффектов временной ряд должен содержать не менее пяти-шести периодов сезонности.

Перейдем теперь к способам удаления сезонного эффекта из ряда. Таких способов два. Первый из них назовем «послетрендовый». Он является логическим следствием рассмотренной выше процедуры оценивания. Для аддитивной модели удаление сезонной компоненты сводится к вычитанию оцененной сезонной компоненты из исходного ряда. Для мультипликативной модели значения ряда делят на соответствующие сезонные индексы.

Второй способ не требует предварительной оценки ни трендовой, ни сезонной компонент, а основывается на использовании разностных операторов.

Разностные операторы

При исследовании временных рядов часто имеется возможность представить детерминированные функции времени простыми рекуррентными уравнениями. Рассмотрим, к примеру, линейный тренд

155

Модель (7.6) не содержит явно параметров, описывающих тренд. Более компактно введенные преобразования можно описать, используя операторы взятия разности назад:

gt gt gt 1 ,

2 gt ( gt ) (gt gt 1) (gt 1 gt 2 ) a1 a1 gt 2gt 1 gt 2 0.

Из последнего соотношения получаем (7.6). Легко видеть, что раз-

ность порядка d исключает из ряда полиномиальный тренд порядка d-1 (см.п.7.4.2).

Пусть теперь ряд содержит сезонный эффект с периодом , так

ного ряда yt детерминированную сезонную компоненту.

Иногда оказываются полезными сезонные операторы более высоких порядков. Так, сезонный оператор второго порядка с периодом есть

τ 2 yt τ ( τ yt ) τ ( yt yt τ ) yt 2yt τ yt 2τ .

Если ряд содержит и тренд, и сезонную составляющую, их можно исключить, последовательно применяя операторы и τ .

Легко показать, что порядок применения этих операторов не существенен:

τ yt ( yt yt τ ) ( yt yt 1) ( yt yt τ 1) τ yt .

Отметим также, что детерминированная часть ряда, состоящая из тренда и сезонной компоненты, после применения операторов

и τ полностью вырождается, т.е. τ yt 0 . Однако записав последнее уравнение в рекуррентной форме, получаем:

156

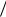
y t = y t - τ + (y t - 1 – y t - τ - 1 ).

Из этого соотношения видно, каким образом ряд можно неограниченно продолжать, имея вначале по крайней мере +1 последовательных значения.

Заметим, исключение тренда и сезонного эффектов как послетрендовым методом, так и взятием разностей искажает случайную составляющую ряда (см. эффект Слуцкого−Юла и п. 7.4.2).

Для рядов с сезонным эффектом предложен ряд адаптивных моделей. Приведем две из них [18]. Модель Тейла−Вейджа предполагает аддитивный сезонный эффект на фоне линейного тренда. Модель ряда имеет вид:

yt gt st ut ; gt gt 1 bt ,

где bt – коэффициент изменения трендовой составляющей. Обозначим ради единообразия gt через at.

Обновление параметров происходит по схеме экспоненциального сглаживания путем взвешенного суммирования текущих значений ряда и прошлых оценок:

Модель Уинтерса предназначена для рядов с линейным трендом и мультипликативным сезонным эффектом. Прогноз ожидае-

Оценки параметров α, β, γ подбирают эмпирически по минимуму суммы квадратов отклонений наблюденных и предсказанных значений.

157

7.6. Линейные модели случайной составляющей временного ряда

Для удобства изложения условимся обозначать здесь случайные величины так, как это принято в математической статистике – строчными буквами.

Случайным процессом X(t) на множестве Т называют функцию, значения которой случайны при каждом t T. Если элементы Т счетные (дискретное время), то случайный процесс часто называют

случайной последовательностью.

Полное математическое описание случайного процесса предпо-

Функции (7.8), (7.9), (7.10) называют конечномерными распределениями случайного процесса.

Построить такую систему функции для произвольного случайного процесса практически невозможно. Обычно случайные процессы задают с помощью априорных предположений о его свойствах, таких как независимость приращений, марковский характер траекторий и т.п.

Процесс, у которого все конечномерные распределения нормальны, называется нормальным (гауссовским). Оказывается, что для полного описания такого процесса достаточно знания одно- и двумерного распределений (7.8), (7.9), что важно с практической точки зрения, поскольку позволяет ограничиться исследованием математического ожидания и корреляционной функцией процесса.

В теории временных рядов используется ряд моделей случайной составляющей, начиная от простейшей – «белого шума», до весьма

158

сложных типа авторегрессии-скользящего среднего и других, которые строятся на базе белого шума.

Прежде чем определять процесс белого шума, рассмотрим последовательность независимых случайных величин, для которой функция распределения есть

Ft1,t2 ,...tn (x1, x2 ,...xn ) Ft1 (x1) Ft2 (x2 ) ... Ftn (xn ) .

Из последнего соотношения следует, что все конечномерные распределения последовательности определяются с помощью одномерных распределений.

Если к тому же в такой последовательности составляющие ее случайные величины X(t) имеют нулевое математическое ожидание и распределены одинаково при всех t T, то это – «белый шум». В случая нормальности распределения X(t) говорят о гауссовском белом шуме. Итак, гауссовский (нормальный) белый шум – после-

довательность независимых нормально распределенных случайных величин с нулевым математическим ожиданием и одинаковой (общей) дисперсией.

Более сложными моделями, широко используемыми в теории и практике анализа временных рядов, являются линейные модели: процессы скользящего среднего, авторегрессии и смешанные.

Процесс скользящего среднего порядка q X q (t) представляет собой конечную взвешенную сумму случайных возмущений:

где εt, εt-1 εt-q – белый шум; b1,b2 ,...,bq – числовые коэффициенты.

Легко видеть из определения, что у процесса скользящего сред-

него порядка q (сокращенно CC(q)) статистически зависимыми являются (q+1) подряд идущих величин X(t), X(t-1),..., X(t-q).

Процессом авторегрессии порядка p (сокращенно АР(р))

называют взвешенную возмущенную сумму p прошлых значений

где εt – белый шум, действующий в текущий момент t; a1,a2,…,ap

– числовые коэффициенты.

159

Выражая последовательно в соответствии с соотношением

(7.12) X(t-1) через X(t-2), . . . , X(t-p-1), затем X(t-2) через X(t-3), . .

. , X(t-p-2) и т.д. получим, что X(t) есть бесконечная сумма прошлых возмущений εt-1, εt-2, … . Из этого следует, члены процесса авторегрессии X(t) и X(t-k) статистически зависимы при любом k.

Процесс АР(1) часто называют процессом Маркова, АР(2) – процессом Юла. В общем случае марковским называют такой процесс, будущее которого определяется только его состоянием в настоящем и воздействиями на процесс, которые будут оказываться в будущем, тогда как его состояние до настоящего момента при этом несущественно. Формально сказанное можно выразить через условные вероятности следующим образом. Рассматривается произвольный момент времени t, t T. Пусть А – произвольное событие, связанное со значениями ряда X ( s ) , s < t , а В – произвольное событие, выраженное через случайные величины X ( s ) , s > t . Случайная последовательность X ( t ) , t T называется марковской, если для любых t,A,B

P(B X (t), A) P(B X (t)) .

Процесс АР(1)

X(t)=aX(t-1)+ ε t

является марковским, поскольку его состояние в любой момент t>t0 определяется через значения процесса εt, если известна величина X ( t 0 ) в момент t0. Формально процесс авторегрессии произвольного порядка Xp(t) также можно считать марковским, если его состо-

янием в момент t считать набор

(X(t), X(t-1), . . . , X(t-p-1)).

Более полно модели СС, АР, а также их композиция: модели авторегрессии-скользящего среднего (АРСС) рассматриваются далее (п.7.9). Заметим только, что все они представляются частными случаями общей линейной модели

где ci – весовые коэффициенты.

Среди моделей случайной составляющей выделим важный класс – стационарные процессы, такие, свойства которых не ме-

160