Назаметдинов Анализ данных 2012
.pdf
С использованием оператора сдвига В имеем: yt aByt εt . От-
сюда yt (1 aB) εt или |
yt |
1 |
εt . Рассматривая |
1 |
при |
|
|
||||
(1 aB) |
(1 aB) |
0<а <1 как сумму бесконечно убывающей геометрической прогрессии со знаменателем аВ, получаем, что
y (1 aB a2 B2 |
...)ε |
t |
ε |
t |
aε |
t 1 |
a2ε |
t 2 |
... . |
(7.22) |
t |
|
|
|
|
|
|
Таким образом, марковский процесс есть частный случай общей линейной модели (7.16) с коэффициентами c j = a j .
Выражение (7.22) можно получить и из (7.21) непосредственно,
выражая yt-1 через yt-2, yt-2 через yt-3 и так далее. Дисперсия yt в соответствии с (7.18) есть
Dyt≡ σ 2y σ ε2 (1 a2 a4 ...) σ ε2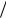 
(1 a2 ) .
Выходит, белый шум с дисперсией σ ε2 порождает в схеме
Маркова случайный процесс с возросшей дисперсией σ ε2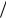 
(1 a2 ) .
Для нахождения автоковариационной функции марковского процесса можно воспользоваться общим выражением (7.19). Однако более нагляден следующий путь. Домножим уравнение (7.21) на yt-1 и возьмем математическое ожидание
M[ yt yt 1] M[ayt2 1] M[εt yt 1] .
Поскольку второе слагаемое в правой части равно нулю в силу некоррелированности εt с прошлым значением ряда yt-1, получаем
|
cov(y , y |
) aσ 2 |
aσ 2 |
|
|
|
|
|
|
t t 1 |
yt 1 |
yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( σ 2y |
σ 2y σ 2y в силу стационарности yt). |
|
|
|
|
|
||
t 1 |
t |
|
|
|
|
|
|
|
Из |
последнего соотношения |
имеем: |
a (cov(y , y |
t 1 |
) |
2 ) r |
, |
|
|
|
|
t |
|
y |
1 |
|
|
т.е. а совпадает с коэффициентом автокорреляции r1.
Умножим (7.21) на yt-k и возьмем математическое ожидание:
) a cov(yt 1, yt k ) .
Заменяя а на r1 и деля на 2y , получаем r k = r 1 r k - 1 . Отсюда rk r1k , k=2,3,…
171
Итак, в марковском процессе все автокорреляции можно выразить через первую автокорреляцию. Поскольку ׀ r1׀<1, автокорреляционная функция марковского процесса экспоненциально убывает при росте k.
Рассмотрим теперь частную автокорреляционную функциюмарковского процесса. Мы получили, что корреляция между двумя членами ряда, отстоящими на два такта, т.е. между yt+2 и yt, выра-
жается величиной r12 . Но yt+2 зависит от yt+1, а yt+1 − от yt. Возникает вопрос, сохранится ли зависимость между yt+2 и yt, если зависимость от срединного члена yt+1 устранена? Соответствующий частный коэффициент корреляции есть
r13.2 |
|
|
r13 |
r12r23 |
. |
|
|
r122 )0.5 |
(1 r232 )0.5 |
||||
|
(1 |
|
||||
Поскольку r13 r12 , r12 r23 r1 , числитель равен нулю. Частные
коэффициенты корреляции для членов ряда, отстоящих на 3,4 и так далее тактов также равны нулю. Таким образом, автокорреляция существует только благодаря корреляции соседних членов, что следует из математической модели марковского процесса.
Графическая иллюстрация полученных результатов представлена на рис. 7.2.
Завершая рассмотрение модели АР(1), отметим, что она весьма часто используется в экономико-математических исследованиях для описания остатков линейной регрессии, связывающей экономические показатели.
Авторерессия второго порядка (процесс Юла)
Модель авторегрессионного процесса Юла АР(2)
yt |
a1 yt 1 a2 yt 2 |
εt |
(7.23) |
||
c использованием оператора сдвига В запишется как |
|||||
yt |
1 |
εt |
a 1 |
(B)εt , |
|
|
|||||
1 a1 B a2 B2 |
|||||
|
|
|
|
||
где а(В) – авторегрессионный оператор, т.е.
172
Рис.7.2. Примеры марковских процессов
и их автокорреляционной и частной автокорреляционной функций
(N=100, а=0,9; 0.3; -0,3; -0,9)
173
а(В) = 1 a1B a 2 B2 . |
(7.24) |
Представим а(В) в виде произведения двух сомножителей |
|
a(B) (1 z1B)(1 z2 B) 1 (z1 z2 )B z1z2 B2 . |
(7.24’) |
Сравнивая (7.24) и (7.24’), видим z1+z2=a1, z1z2= –a2, так что z1 и
z2 есть корни квадратного уравнения |
|
z2 – a1z – a2 = 0. |
(7.25) |
Свойства модели (7.23) зависят от z1 и z2. |
|
Для стационарности процесса (7.23) необходимо, чтобы корни z1 и z2 лежали внутри единичной окружности (случай комплексных
корней при a12 4a2 < 0), либо были меньше единицы (случай дей-
ствительных |
корней |
при |
a12 4a2 ≥ |
0), |
что |
обеспечивается при |
||||
׀a1׀<2 и a2<1–׀a1׀. |
|
|
|
|
|
|
|
|
|
|
Пусть z |
и z действительны и различны. Разложим a 1 (B) на |
|||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
простые дроби |
|
|
|
|
|
|
|
|
|
|
|
a 1 (B) |
|
m1 |
|
|
m2 |
|
, |
(7.26) |
|
|
1 z1B |
|
|
|
||||||
|
|
|
1 |
z2 B |
|
|||||
где m1 z1 (z1 z2 ), |
m2 z2 (z1 z2 ) . |
|
|
|
||||||
Рассматривая отдельные слагаемые в (7.26) как суммы бесконечных геометрических прогрессий (z1, z 2 < 1), получим
|
|
|
|
|
|
a 1(B) m1 z1 j B j m2 |
z2j B j (m1z1 j m2 z2j )B j . |
||||
j |
0 |
j |
0 |
j |
0 |
Выходит, АР(2) есть частный случай общей линейной модели (7.16) с коэффициентами
c j m1z1 j m2 z2j (z1 j 1 z2j 1) /(z1 z2 ) .
Рассмотрим теперь автокорреляционную функцию процесса Юла. Умножим (7.23) по очереди на yt-1 и yt-2, возьмем математиче-
ские ожидания и разделим на σ2y . В итоге получим:
r1 a1 a2r1,
r2 a1r1 a2 .
174
Из этих уравнений можно найти а1 и а2, если известны первые две автокорреляции и, наоборот, по известным а1 и а2 найти r1 и r2:
|
|
|
r1 |
a |
, r2 |
|
a2 |
|
a2 . |
|
|
||||
|
|
|
1 |
|
|
1 |
|
|
|
||||||
|
|
|
1 r2 |
|
1 a2 |
|
|
|
|||||||
Умножим (7.23) на yt и возьмем математическое ожидание: |
|||||||||||||||
2 |
a cov(y , y |
|
) a cov(y , y |
|
) |
2 |
a r 2 |
a r 2 |
2 . |
||||||
y |
1 |
t t 1 |
|
2 |
|
t t 2 |
|
|
1 1 y |
2 2 y |
|
||||
Подставим в последнее соотношение выражения для r1 и r2: |
|||||||||||||||
|
|
2 |
|
|
|
|
(1 a2 ) |
|
|
|
2 . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y |
|
(1 a2 )(1 |
a1 a2 )(1 a1 a2 ) |
|
|
||||||||
|
|
|
|
|
|
||||||||||
Дисперсия не может быть отрицательной, что имеет место при
|
a2 |
|
1, |
a2 a1 1, |
a2 a1 1. |
|
|
Умножая (7.23) на yt k , k 2 , получим рекуррентное уравнение
rk a1rk 1 a2rk 2 0 , |
(7.27) |
из которого можно найти автокорреляции высоких порядков через первые автокорреляции. Тем самым полностью определяется коррелограмма процесса Юла.
Исследуем вид коррелограммы процесса АР(2). Выражение (7.27) можно рассматривать как разностное уравнение второго порядка относительно r с постоянными коэффициентами.
Общее решение такого уравнения имеет вид |
|
|
rj d1z1 j d2 z2 j , |
(7.28) |
|
где d1 и d2 − произвольные числа, |
j=1,2,3 и т.д., а z1 |
и z2 – корни |
характеристического уравнения |
|
|
z2 a1z a2 |
0 , |
(7.29) |
где z – комплексная переменная.
Отметим, что уравнения (7.25) и (7.29) совпадают.
Таким образом, в случае действительных корней коррелограмма АР(2) представляет собой, как видно из (7.26), смесь двух затухающих экспонент. В случае комплексных корней коррелограмма процесса АР(2) оказывается затухающей гармоникой.
Рассмотрим теперь, как ведет себя частная автокорреляционная функция процесса Юла. Отличным от нуля оказывается лишь ко-
175
эффициент r13.2, равный a2. Частные корреляции более высоких порядков равны нулю (подробнее этот процесс рассматривается дальше). Таким образом, частная коррелограмма процесса обрывается сразу после лага, равного единице.
В заключение отметим, что модели АР(2) оказались приемлемыми при описании поведения циклической природы, прообразом которого служит маятник, на который воздействуют малые случайные импульсы. Амплитуда и фаза такого колебательного процесса будут все время меняться.
Авторегрессия порядка р
Процесс авторегрессии порядка р, кратко АР(р), описывается выражением
yt εt a1 yt 1 a2 yt 2 ... ap yt p |
(7.30) |
или |
|
(1 a1 B a2 B2 ... a p B p ) yt a(B) yt εt . |
(7.30’) |
По аналогии с тем, как строилась автокорреляционная функция
процессов АР(1) и АР(2), последовательно умножим уравнение (7.30) на yt-k (k=1,2,…, p), возьмем математическое ожидание и раз-
делим на σ2y . Получим систему уравнений относительно коэффициентов корреляции:
rk a1rk 1 a2rk 2 |
... ap rk p , k 1,2,..., p . |
|
|
|
(7.31) |
||||||||
Учитывая, что r – k = r k , и вводя матричные обозначения |
|
|
|||||||||||
1 |
r |
r |
r |
p 1 |
|
r |
|
a |
|
|
|||
|
|
1 |
2 |
|
|
|
1 |
|
|
1 |
|
|
|
r1 |
1 |
r2 |
rp 2 |
|
r2 |
|
a2 |
|
, |
||||
P |
|
|
|
|
|
, |
r |
|
, |
a |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
rp 2 |
rp 3 |
1 |
|
|
|
|
|
|
|
|
|
rp 1 |
|
rp |
a p |
|
|||||||||
запишем (7.31) в виде |
|
P a = r . |
|
|
|
|
|
|
|
(7.32) |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Систему уравнений (7.32) называют системой Юла−Уокера. Из
нее находим, что |
|
a=Р-1 r. |
(7.33) |
176
Таким образом, зная первые р автокорреляций временного ряда, можно найти по (7.31) автокорреляции более высокого порядка, т.е. полностью восстановить автокорреляционную функцию (что уже отмечалось при анализе процессов АР(1) и АР(2)).
Поведение автокорреляционной функции зависит от корней z1, z2,…,zp характеристического многочлена
z p a1z p 1 ... ap 1z ap 0 .
Для стационарного процесса корни многочлена лежат внутри единичного круга, т.е. | zi |1, i=1,2,…,p.
Заметим, что характеристический многочлен часто записывают в иной форме:
1 a1λ a2λ2 ... ap λ p 0 .
Легко видеть, что корни этих уравнений связаны соотношением z=1/, так что условие стационарности АР-процесса в этом случае меняется на противоположное: | λ i |>1, i=1,2,…,p.
Обычно коррелограмма процесса АР(р) состоит из совокупности затухающих экспонент и затухающих гармоник.
Если у процесса АР(2) частная автокорреляция членов ряда, разделенных двумя или большим числом членов, равна нулю, то у процесса АР(р) нулю равны автокорреляции порядка р и выше. Выходит, частная коррелограмма процесса АР(р) должна равняться нулю, начиная с некоторого момента. Правда, надо заметить, что этот факт имеет место для бесконечного ряда. Для конечных реализаций указать место обрыва коррелограммы часто затруднительно.
Итак, для процесса АР(р) частная автокорреляционная функция обрывается на лаге р, тогда как автокорреляционная функция плавно спадает.
7.10.2. Процессы скользящего среднего
Обобщенная линейная модель (7.16) для процессов скользящего среднего содержит лишь конечное число членов, т.е. в (7.16) ck=0
при k > q . Модель приобретает вид
yt εt b1εt 1 ... bqεt q (1 b1B ... bq Bq )εt b(B)εt . (7.34)
177
(В (7.34) коэффициенты cj переобозначены через – bj, b(B) – опе-
ратор скользящего среднего).
Соотношение (7.34) определяет процесс скользящего среднего порядка q, или сокращенно СС(q).
Найдем дисперсию процесса СС(q):
σ 2y M[(yt M[yt ])2 ] M[ yt2 ] (1 b12 b2 |
2 ... bq q )σ ε2 . |
t |
|
Заметим, что в вышеприведенном выражении отсутствуют смешанные произведения вида bibj M[εi ε j ] , поскольку они равны нулю
в силу некоррелированности возмущений в разные моменты времени.
Для нахождения автокорреляционной функции процесса СС(q) последовательно умножим (7.34) на y t - k , возьмем математическое ожидание
M[ yt yt k ] M[(εt ... |
bq εt q )(εt k ... |
bqεt k q )]. |
(7.35) |
В правой части выражения (7.35) останутся только те члены, которые отвечают одинаковым временным тактам.
Следовательно, выражение (7.35) есть
|
|
q k |
|
|
||
|
( bk bjbj k )σ ε2 , |
k 1,2,...,q; |
(7.36) |
|||
cov(yt , yt k ) |
j |
1 |
|
|
||
|
|
|
|
|
||
|
k q. |
|
|
|||
|
0 , |
|
|
|||
Поделив (7.36) на σ2y , получим |
|
|
||||
|
q k |
|
|
|
|
|
|
bk bjbj k |
|
|
|||
rk |
j 1 |
|
|
, k 1,2,...,q, rk 0, k q . |
(7.37) |
|
1 b12 ... bq |
2 |
|||||
Тот факт, что |
автокорреляционная функция процесса |
СС(q) |
||||
имеет конечную протяженность (q тактов) – характерная особенность такого процесса. Если r1,r2,…,rq известны, то (7.37) можно в принципе разрешить относительно параметров b1,b2,…,bq. Уравнения (7.37) нелинейные и в общем случае имеют несколько решений, однако условие обратимости выделяет единственное решение.
178
Как уже отмечалось, обратимые процессы СС можно рассматривать как бесконечные АР-процессы АР( ). Следовательно, частная автокорреляционная функция процесса СС(р) имеет бесконечную протяженность. Итак, у процесса СС(q) автокорреляционная функция обрывается на лаге q, тогда как частная автокорреляционная функция плавно спадает.
7.10.3. Комбинированные процессы авторегрессии-скользящего среднего
Хотя модели АР(р) и СС(q) позволяют описывать многие реальные процессы, число оцениваемых параметров может оказываться значительным. Для достижения большей гибкости и экономичности описания при подборе моделей к наблюдаемым временным рядам полезными оказались смешанные модели, содержащие в себе и авторегрессию, и скользящее среднее. Эти модели предложены
Боксом и Дженкинсом и получили название модели авторегрессиискользящего среднего (сокращенно АРСС(р, q) либо ARMA(p,q)):
yt a1 yt 1 a2 yt 2 ... ap yt p εt b1εt 1 b2εt 2 ... bqεt q , |
(7.38) |
или более компактно: |
|
a(B) yt b(B)εt , |
(7.38’) |
где а(В) − авторегрессионный оператор порядка р; b(В) − оператор скользящего среднего порядка q.
Модель (7.38’) может быть записана и так:
yt |
a 1(B)b(B)εt |
b(B) |
εt |
|
1 b1B ... bq Bq |
εt . (7.38’’) |
|||||||||||
a(B) |
1 a1B ... ap B p |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рассмотрим простейший смешанный процесс АРСС(1,1). |
|||||||||||||||||
Согласно (7.38’’) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
yt |
1 b1B |
|
εt (1 b1B)(1 a1B a12 B2 |
...)εt |
|
|
|
||||||||||
|
|
|
(7.39) |
||||||||||||||
|
|
1 a1B |
|
|
|
|
|
|
|
|
|
|
|
||||
ε |
t |
(a b )ε |
t 1 |
a (a b )ε |
t 2 |
a 2 |
(a b )ε |
t 3 |
.... |
||||||||
|
1 |
|
1 |
1 1 |
1 |
1 |
1 1 |
|
|||||||||
Из соотношения (7.37) видно, что модель АРСС(1,1) является частным случаем общей линейной модели (7.16) с коэффициентами cj= a1j 1 (a1 b1 ), j 0 .
179
Из (7.39) легко получить выражение для дисперсии yt :
σ y |
2 M[ y2 ] [1 (a1 |
b1 )2 a12 (a1 b1 )2 |
...]σε |
2 |
||||
|
[1 (a1 b1)2 (1 a12 a14 ...)]σε |
2 |
|
|||||
|
|
1 |
(a1 b1)2 |
σ |
2 |
1 2a1b1 b12 |
σ 2. |
|
|
2 |
|
|
|||||
|
|
|
ε |
2 |
ε |
|
||
|
|
|
1 a1 |
|
|
1 a1 |
|
|
|
|
|
|
|
|
|
|
|
Для получения корреляционной функции воспользуемся тем же приемом, что и при анализе моделей авторегрессии. Умножим обе части модельного представления процесса АРСС(1,1)
y t = a 1 y t - 1 + ε t – b 1 ε t - 1
на yt-k (k >0) и возьмем математическое ожидание:
cov(yt , yt k ) a1 cov(yt 1, yt k ) cov(εt , yt k ) b1 cov(εt 1, yt k ) .
C учетом того, что второе слагаемое в правой части равенства равно нулю, имеем:
a c |
k 1 |
a k 1c , |
k 2; |
|||
|
1 |
1 |
|
1 |
|
|
ck |
|
|
|
|
|
k 1. |
a1σ 2y b1σ |
2 |
, |
||||
|
|
|
|
|
|
|
Поделив ковариации ck на дисперсию 2y , получаем выражения для автокорреляции:
r1 |
|
(1 a1b1 )(a1 b1 ) |
, |
rk a1k 1r1, |
k 2 . (7.40) |
|
|||||
|
|
(1 a12 ) |
|
|
|
Аналогично может быть построена автокорреляционная функция для общей модели АРСС(р,q). Оказывается, что при q<р вся автокорреляционная функция будет выражаться совокупностью затухающих экспонент и/или затухающих синусоидальных волн, а при q > p будет q-p значений r1,r2,…,rq-p, выпадающих из данной схемы.
7.10.4. Модель авторегрессии-скользящего среднего для нестационарного временного ряда
Модель АРСС можно обобщить на случай нестационарных временных рядов, допускающих приведение к стационарному виду. Выделяют два типа подобных рядов. К первому типу относят ряды
180