
Назаметдинов Анализ данных 2012
.pdfвида yt gt ut , содержащие детерминированный тренд gt и ста-
ционарный процесс ut. Говорят, что ряд yt является стационарным
относительно детерминированного тренда gt, иначе TS-рядом
(trend stationary), если ряд y t – g t является стационарным. Рассмотренные выше модели АРСС применялись, по сути дела, к TSпроцессам.
Ко второму типу относят ряды, содержащие стохастический
тренд. Ярким примером такого процесса являются «случайные блуждания» (random walk):
y t = y t - 1 + εt . (7.41)
С использованием оператора сдвига модель (7.41) принимает вид
|
|
|
|
εt |
|
|
|
|
|
yt |
εt εt 1 ... εt j . |
(7.41’) |
|
|
|
|
1 B |
|||
|
|
|
|
j 0 |
|
|
|
|
|
|
|
|
|
Из (7.41’) |
|
видно, |
что процесс (7.41) расходящийся, |
посколь- |
||
|
|
|
|
|
|
|
ку σ y |
2 σε |
2 |
. Характеристическое уравнение этого процесса |
|||
|
j 1 |
|
|
|
|
|
имеет корень, равный единице, т.е. имеет место пограничный случай, когда корень характеристического уравнения оказался на границе единичной окружности. В то же время, если перейти к первым разностям ut yt yt yt 1 , то процесс ut окажется стацио-
нарным – ut εt . Существуют процессы, для которых стационар-
ными оказываются разности более высокого порядка.
Временной ряд yt называется интегрированным порядка d (обозначается I(d)), если ни сам ряд, ни его разности yt, 2 yt,…,
d 1 yt не являются TS-рядом, тогда как разность d yt порядка d обладает свойством стационарности. Заметим, что I(0) соответствует исходному стационарному ряду.
Интегрированные ряды образуют класс разностно-стацио-
нарных, иначе DS-рядов (differencе stationary).
Пусть нестационарный авторегрессионный оператор aH (B) в модели АРСС имеет один или несколько корней, равных единице,
181
т.е. речь идет о DS-ряде, интегрированном порядка d. Иными словами, aH (B) является нестационарным оператором авторегрессии
порядка p+d; d корней уравнения a H (B )=0 равны единице, а остальные р корней лежат вне единичного круга. Тогда можно записать, что
aH (B) a(B)(1 B)d ,
где a(B) – стационарный оператор авторегрессии порядка р (с корнями λ вне единичного круга).
Используя оператор разности
yt yt yt 1 = (1-B)yt,
нестационарный процесс АРСС порядка d можно записать как
a(B) d yt b(B)εt . |
(7.42) |
Для разности xt порядка d , т.е. xt d yt , модель
a(B)xt b(B) t
описывает уже стационарный обратимый процесс АРСС(р, q).
Для того чтобы от ряда разностей вернуться к исходному ряду,
требуется оператор S, обратный : S 1 (1 B) 1 B j .
j 0
Этот оператор называют оператором суммирования, поскольку S y t = y t + y t - 1 + y t - 2 + … . Если же исходной является разность порядка d, то для восстановления исходного ряда понадобится d- кратная итерация оператора S, иначе d-кратное суммирование (интегрирование). Поэтому процесс (7.42) принято называть процессом АРИСС либо АРПСС (ARIMA – в англоязычной литературе),
добавляя к АРСС термин интегрированный либо проинтегрированный. Кратко модель (7.42) записывают как АРИСС(р,d,q), где р –
порядок авторегрессии, d – порядок разности, q – порядок скользящего среднего. Ясно, что при d = 0 модель АРИСС переходит в модель АРСС.
На практике d обычно не превышает двух, т.е. d 2.
Модель АРИСС допускает представление, аналогичное общей линейной модели, а также в виде «чистого» процесса авторегрес-
182

сии (бесконечного порядка). Рассмотрим, к примеру, процесс АРИСС (1, 1, 1):
(1 aB)(1 B) yt (1 bB)εt . |
(7.43) |
Из (7.43) следует, что
t (1 aB)(1 B) [1 (1 a)B aB2 ] (1 bB b2 B2 ...) yt
1bB
[1 (1 a b)B (b a)(1 b)B2 (b a)(1 b)B3 ...] yt .
Отсюда
yt [a (1 b)] yt 1 (b a)(1 b) yt 2 (b a)(1 b)byt 3 ... εt .(7.44)
Проверка гипотезы о наличии единичного корня
Для проверки гипотезы о наличии единичного корня может быть использован тест Дики−Фуллера (Dickey-Fuller), далее DF-
тест [19]. Рассматриваются простейшее авторегрессионное уравне-
ние и две его модификации: |
|
|
|
yt ayt 1 |
εt , |
(7.45a) |
|
yt |
ayt 1 |
b εt , |
(7.45б) |
yt |
ayt 1 |
b ct εt . |
(7.45в) |
Заметим, что модель (7.45б) при а =1 принято называть моделью случайных блужданий с дрейфом. Расписывая рекуррентное выражение (7.45б) от начального значения у0, получаем выражение
t
yt y0 bt i
i 1
для процесса с линейным трендом и растущей дисперсией.
В DF-тесте проверяются нулевая Н0: а=1 (уравнение содержит
единичный корень – процесс случайных блужданий) и альтернативные гипотезы Н1. Для уравнения (7.45а) Н1: |a|< 1 (ряд стационарный); для уравнения (7.45б) – Н1: |a |<1 и b 0 (процесс АР(1) с
ненулевым постоянным членом); для уравнения (7.45в) Н1 означает авторегрессионный процесс первого порядка АР(1) с ненулевым постоянным членом и детерминированным линейным трендом.
Процедура проверки следующая [19]. По результатам наблюдений методом наименьших квадратов оценивается то или иное урав-
183
нение из (7.45а)–(7.45в) и вычисляется статистика tDF = (aˆ 1) / saˆ ,
которая сравнивается затем с критическими значениями теста Ди- ки–Фуллера (табл. 7.2). Н0 отвергается, если расчетное значение t- статистики меньше критического значения. Заметим, что использование t-статистики здесь некорректно, поскольку при а =1 она не подчиняется распределению Стьюдента.
На практике часто предпочитают работать с рядом разностей, так что гипотезу Н0 формулируют в виде yt εt . Альтернативные гипотезы принимают вид
yt kyt 1 b ct εt ,
где k=а-1, b=c=0 для уравнения (7.45а); с=0 – для (7.45б). |
|
ˆ |
/ s ˆ . |
Статистика Дики–Фуллера запишется теперь как tDF= k |
|
|
k |
Данная статистика оказывается применимой для тестирования гипотезы о неединственности единичного корня. Если Н0-гипотеза не отвергается для первых разностей, то переходят к разностям
второго порядка 2 yt yt yt 1 .
В качестве объясняющей переменной выступает yt 1 . Если по
результатам нового теста Н0 отвергается, то принимается гипотеза о единственности единичного корня. Иначе можно говорить о наличии как минимум двух единичных корней. В этом случае переходят к разностям третьего порядка и так далее.
|
|
|
|
Таблица 7.2 |
Уровень |
|
Размер выборки |
|
|
значимости |
25 |
50 |
100 |
|
|
|
Уравнение (а) |
|
|
0,01 |
-2,66 |
-2,62 |
-2,60 |
-2,58 |
0,05 |
-1,95 |
-1,95 |
-1,95 |
-1,95 |
|
|
Уравнение (б) |
|
|
0,01 |
-3,75 |
-3,58 |
-3,51 |
-3,43 |
0,05 |
-3,00 |
-2,93 |
-2,89 |
-2.86 |
|
|
Уравнение (в) |
|
|
0,01 |
-4,38 |
-4,15 |
-4,04 |
-3,96 |
0,05 |
-3,60 |
-3,50 |
--3,45 |
-3,41 |
184
7.11. Прогнозирование по модели АРИСС
Как уже отмечалось, процессы АРИСС допускают представление в виде обобщенной линейной модели (7.16).
Пусть в текущий момент времени t мы хотим найти будущее (прогнозное) значение ряда в момент t+τ (τ>0). Естественно искать его в виде
|
1 |
|
yt c j εt j c j εt j c j εt j . |
||
j 0 |
j 0 |
j |
Ожидаемое значение yt+τ, обозначаемое как yt (τ) , есть
1 |
|
yt ( ) = M[ yt ] c j M[εt j ] c j M[εt j ] . |
|
j 0 |
j |
Первая сумма в правой части последнего соотношения содержит лишь будущие возмущения, и для них математическое ожидание равно нулю по определению. Что же касается второго слагаемого, то возмущения здесь уже состоялись, так что
M[εt j ] εt j , |
j τ . |
Таким образом, |
|
|
|
yt (τ) = c j εt j . |
(7.46) |
j |
|
Ошибка прогноза, представляющая расхождение между прогнозным значением и его ожиданием есть
|
|
1 |
|
|
|
ut (τ) yt |
yt (τ) c jεt j . |
|
|
||
|
|
j 0 |
|
|
|
Дисперсия ошибки отсюда есть |
|
|
|
|
|
σ2ut ( ) M[(u (τ))2 |
] 1 c2 |
c2 |
... c2 |
σ2 . |
(7.47) |
t |
1 |
2 |
1 |
ε |
|
Заметим, что формула (7.47) получена в предположении, что коэффициенты модели (7.16) не содержат ошибок и механизм, порождающий ряд, не изменится к моменту t+τ.
Прогнозирование по соотношению (7.46) затруднительно, поскольку требует знания всех прошлых возмущений. К тому же ско-
185
рость затухания c j часто оказывается недостаточной, не говоря уже о нестационарных процессах, для которых ряды c j расходятся.
Поскольку модель АРИСС допускает и другие представления, рассмотрим возможности их использования для прогнозирования.
Пусть модель задана непосредственно разностным уравнением
yt =a1 yt - 1 +a2 yt - 2 +…+a p + d yt - ( p + d ) –b1 εt 1 –…– bq εt q + εt . (7.48)
По |
известным значениям ряда (результатам наблюдений) |
||
~ ~ |
~ |
и оцененным значениям возмущений |
εˆt ,εˆt 1,..., |
yt , yt 1 |
,..., yt ( p d ) |
||
εˆ t q , опираясь на рекуррентную формулу (7.48), можно оценить
ожидаемое значение ряда в момент t+1: |
|
|
|||
ˆ |
~ |
~ |
~ |
ˆ |
ˆ |
yt (1) |
a1 yt a2 yt 1 |
... ap d yt ( p d ) b1εt ... bqεt 1 q . (7.49) |
|||
При прогнозировании на два такта вновь используем рекуррентное соотношение (7.48), где в качестве наблюденного значения ряда в момент t+1 следует взять предсказанную по (7.49) величину
ˆ |
, т.е. |
ˆ |
~ |
, и так далее. |
yt (1) |
yt (1) |
yt 1 |
Оценка (7.47) является лишь нижней границей «прогностической силы» модели. На практике стараются набрать некоторую статистику прогнозов. Для этого исходную выборку объема N разбивают на две: рабочую (начальную t = 1,2,…, N1) и контрольную (начальную t = N1+1,. N1+2,…, N). Оценки параметров модели получают по рабочей выборке, оценку точности прогнозов получают по контрольной выборке. Пусть прогноз осуществляется на τ тактов (τ <N – N 1 ). Модель пересчитывается N – N 1 – τ раз. При каждом пересчете объем рабочей выборки прирастает на один такт, либо остается неизменным (выборка при этом сдвигается вправо на такт):
t = 2,3,…, N1+1; t=3,4,…, N1+2;…; t = τ , τ +1,…,N–τ+1.
Для оценки точности прогнозов используется в основном среднее значение суммы квадратов отклонений прогнозных значений ряда от фактических.
186
7.12.Технология построения моделей АРИСС
Описанные выше теоретические схемы строились в предположении, что временной ряд имеет бесконечную предысторию, тогда как реально исследователю доступен ограниченный объем наблюдений. Поэтому с позиций практического применения теории анализа временных рядов определяющее значение имеют вопросы корректной спецификации модели АРИСС( p , d , q ) (ее идентификации) и последующего оценивания ее параметров.
Идентификация модели
Цель идентификации – получить некоторое представление о величинах p, d, q и о параметрах модели. Идентификация модели распадается на две стадии:
1.Определение порядка разности d исходного ряда yt .
2.Идентификация модели АРСС для ряда разностей d yt .
Основной инструмент, используемый на обеих стадиях – автокорреляционная и частная автокорреляционная функции. Если автокорреляционная функция затухает медленно и почти линейно, то это свидетельствует о нестационарности процесса. В этом случае от исходного ряда переходят к разностям. Считается, что порядок разности d, обеспечивающий стационарность, достигнут тогда, ко-
гда автокорреляционная функция процесса ut d yt падает до-
вольно быстро. На практике обычно d <3 .
После того как будет получен стационарный ряд разностей порядка d, изучают общий вид автокорреляционной и частной автокорреляционной функций этих разностей. Опираясь на теоретические свойства этих функций можно выбрать значения p и q для АР и СС операторов.
Далее при выбранных p и q строятся начальные оценки параметров авторегрессии a =( a 1 , a 2 , … , a p ) и скользящего среднего b =(b 1 ,b 2 ,… , b q ). Для авторегрессионных процессов используются уравнения Юла−Уокера, где теоретические автокорреляции заменены на их выборочные оценки. Для процессов скользящего среднего порядка q только первые q автокорреляций отличны от нуля (см.7.37). Заменяя ri их выборочными оценками rˆ и решая
187

получающиеся уравнения относительно b1,b2 ,...,bq , получим оцен-
ˆ
ку b . Эти предварительные оценки можно использовать как начальные значения для получения на следующих шагах более эффективных оценок.
Для смешанных процессов АРСС процедура оценивания услож-
няется. Так, для рассмотренного процесса АРСС(1,1) параметры a1 и b1, точнее их оценки, получаются из (7.40) с заменой r1 и r2 их
выборочными оценками.
В общем случае вычисление начальных оценок процесса АРСС(p,q) представляет многостадийную процедуру. Отметим только, что для практики особый интерес имеют АР и СС процессы 1-го и 2-го порядков и простейший смешанный процесс АРСС(1,1).
Об адекватности оцененной модели судят по остаткам, которые согласно предпосылкам при больших N являются белым шумом.
Заметим, что оценки автокорреляций, на основе которых строятся процедуры идентификации, могут иметь большие дисперсии (особенно в условиях недостаточного объема выборки – несколько десятков наблюдений) и быть сильно коррелированны. Поэтому говорить о строгом соответствии теоретической и эмпирической автокорреляционных функций не приходится. Это приводит к затруднениям при выборе p, d, q, поэтому для дальнейшего исследования могут быть выбраны несколько моделей.
Для сравнения моделей между собой предложен ряд критериев. Наибольшее распространение получили два из них: информацион-
ный критерий Акаике (AIC) и байесовский информационный критерий Шварца (SBIC). Оба критерия представляют сумму двух сла-
гаемых, первое из которых зависит от остаточной суммы квадратов
sˆ 2 , второе – моделирует штраф за уменьшение числа степеней свободы из-за включения в модель дополнительных параметров:
AIC ln sˆ2 2 p q ; SBIC ln sˆ2 ln N p q .
N N
Критерий Шварца в отличие от критерия Акаике обеспечивает состоятельность оценок, но проигрывает последнему с точки зрения их эффективности.
188

Предпочтение отдается модели с меньшим значением критерия.
7.13. Нелинейные по возмущениям модели
Рассмотренные выше линейные модели оказываются нередко неприемлемыми при описании реальных процессов. Так, в финансовых рядах случайные отклонения от трендовой составляющей часто идут сериями то с большим размахом («возмущенный рынок»), то с малым («спокойный рынок»), образуя тем самым «сгу-с- тки», кластеры, на графике ряда. Для описания подобного рода процессов используются модели авторегрессионной условной гетероскедастичности (ARCH-модели). Эти модели существенно опираются на понятие условной дисперсии.
Пусть 2 |
D[u |
u |
,...,u |
] M[u2 |
|
u |
,...,u |
] – условная дис- |
|
||||||||
t |
t |
t 1 |
t p |
t |
|
t 1 |
t p |
|
|
|
|
|
|
|
|
|
|
персия случайного компонента u ряда (остатков после исключения детерминированной составляющей). Полагают, что условная дисперсия текущего момента зависит от предыстории следующим образом:
σ2 |
a |
a u2 |
... a |
u2 |
. |
|
|
(7.50) |
||||
t |
|
0 |
|
1 t 1 |
|
|
t p |
t p |
|
|
|
|
Значения ut описываются при этом моделью |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
u ε |
(a |
|
a u2 |
|
... a |
u2 |
) 2 |
, |
(7.51) |
|||
t |
t |
0 |
1 t 1 |
|
t p t p |
|
|
|
|
|||
где εt – гауссовский белый шум, т.е. εt |
N 0, 1 . |
|
|
|||||||||
Модель (7.50)-(7.51) называют авторегрессионной условно гетероскедастичной моделью порядка р и обозначают ARCH(p).
Заметим, что безусловная дисперсия процесса (7.51) является
неизменной для любого момента времени. Проиллюстрируем это утверждение на примере модели ARCH(1):
|
ut εt (a0 a1ut2 1)1 2 . |
|
|
(7.52) |
||
Возведя (7.52) в квадрат, выражая ut2 1 через |
ut2 2 |
, ut2 2 – через |
||||
u 2 |
и так далее, получаем: u2 |
a (ε2 |
a ε2 |
a2ε2 |
...) . Учиты- |
|
t 3 |
t |
0 t |
1 t 1 |
|
1 t 2 |
|
вая центрированность и некоррелированность элементов бе-лого шума, получаем:
189
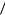
D[ut ] M[ut2 ] a0 |
(1 a1) при условии |
|
a1 |
|
1. |
|
|
Проверка ut на гетероскедастичность производится следующим образом: оценивается регрессия
ut2 b0 b1 ut2 1 ... bput2 p vt ,
с последующим тестированием гипотезы H0: b0=b1=…bp=0. Дальнейшим обобщением является обобщенная авторегресси-
онная условно гетероскедастичная модель порядка (p,q) – обозна-
чается GARCH(p,q), в которой ряд |
ut2 |
и его условная дисперсия |
||||||
описываются с помощью процесса АРСС(p,q): |
|
|
||||||
σ2 |
a |
a u2 |
... a u2 |
|
b σ2 |
... b σ2 |
. |
|
t |
0 |
1 t 1 |
p t p |
|
1 t 1 |
q t q |
|
|
Для оценки ARCH/GARCH-моделей используется метод максимального правдоподобия.
Вопросы и упражнения.
1.Какое свойство является определяющим в дефиниции временного ряда?
2.В чем состоит различие между моментными и интервальными временными рядами?
3.Какие типы рядов рассматриваются в данном пособии?
4.Какие научные дисциплины занимаются изучением процессов, протекающих во времени?
5.Какую модель тренда следует использовать, если постоянным сохраняется: а) абсолютный прирост исследуемой переменной; б) относительный прирост?
6.Какая гипотеза относительно поведения ряда лежит в основе логистической кривой?
7.Чем чревато использование высоких степеней в полиномиальных моделях тренда?
8.Гауссовский случайный процесс сгладили методом скользящего среднего с шириной окна, равной 7. Тот же процесс сгладили
190
