Назаметдинов Анализ данных 2012

CCА предполагает активное участие исследователя в процессе его применения. Опыт показывает, что чем больше промежуточных результатов удается "увидеть", тем более полным оказывается решение поставленной задачи.

Вопросы и упражнения

1.Приведите определение главной компoненты.

2.Какое максимальное число главных компонент можно выделить для матрицы исходных данных порядка 80*15 (N=80, n=15)?

3.Приведите аналитическое выражение эллипсоида рассеяния в двумерном случае.

4.Какова дисперсия нормированных переменных?

5.Когда возможно построение доверительного интервала собственных значений ковариационной матрицы?

6.Какова дисперсия i-й главной компоненты?

7.Как найти главные компоненты для диагональной матрицы исходных признаков?

8.Для каких задач целесообразно использовать метод главных компонент?

9.Оцените долю дисперсии, приходящуюся на первую главную компоненту, если ковариационная матрица исходных переменных

10. Что такое «траекторная матрица»?

242

11. ФАКТОРНЫЙ АНАЛИЗ

В отличие от метода главных компонент факторный анализ заранее объясняет ковариационную (либо корреляционную) матрицу исходных переменных (признаков) наличием небольшого числа гипотетических факторов, присутствующих в исходных переменных. На языке корреляций это можно интерпретировать следующим образом. Вначале анализируется на значимость исходная корреляционная матрица, т.е. отличается ли корреляционная матрица значимо от единичной. Если это имеет место, то возникает вопрос:

существует ли скрытая, иначе латентная, случайная величина y1

такая, что попарные корреляции между исходными переменными станут равными нулю, если влияние y1 уже учтено? Пусть после этого элементы корреляционной матрицы все еще отличны от нуля. Тогда пытаются найти две случайные величины y1 и y2 такие, что корреляции между исходными переменными станут нулевыми, если влияние y1 и y2 уже учтено, и так далее.

Тем самым корреляция между n наблюдаемыми признаками x1, x2 ,...,xn связывается с тем фактом, что эти признаки зависят от меньшего числа других, непосредственно неизмеряемых переменных y1, y2 ,..., yn m n , которые принято называть общими факторами.

11.1. Модель факторного анализа

В общем случае нельзя гарантировать, что каждый исходный признак зависит лишь от m общих факторов, одних и тех же для всех признаков. Поэтому в факторном анализе постулируется, что наблюдаемый признак xi (i=1,2,…,n) зависит также и от некоторой характерной для себя остаточной (шумовой) случайной компоненты ui . Итак, линейная модель факторного анализа [11] имеет вид:

243

где коэффициенты aij называют нагрузкой j-го общего фактора на i-й исходный признак, а матрицу A aij , i =1,2,…, n; j =1,2,.., m –

факторным отображением, либо матрицей факторных нагрузок.

Предпосылки факторного анализа

Предполагают, что исходные признаки подчиняются многомерному нормальному распределению; общие факторы некоррелированы, а их дисперсии равны единице, следовательно, корреляцион-

ная матрица Cy общих факторов является единичной, т.е. Cy 1 ;

характерные (остаточные) факторы u1,u2 ,...,un – нормально распределенные случайные величины, не зависимые друг от друга и от общих факторов. Это означает, что корреляционная матрица V характерных факторов имеет диагональный вид. Все случайные величины имеют нулевое математическое ожидание.

Факторные нагрузки aij и дисперсии vii2 характерных факторов

являются неизвестными параметрами, подлежащими оценке.Вводя векторные обозначения:

Ковариационная матрица Cx исходных признаков с учетом их центрированности по определению есть

Cx = M[x x ' ] ,

где математическое ожидание берется по множеству реализаций вектора x. Подставим в Cx выражение (11.1а):

Cx = M[(Ay+u)(Ay+u)′] = M[(Ay+u)(y′A′+u′)].

Раскрывая скобки в последнем выражении и учитывая, что общие и характерные факторы некоррелированы и, следовательно, M[u′y]=0, M [y u ′]=0, а также неслучайный характер матрицы A, что позволяет выносить А за знак М, получаем

C x = A M[y y ′ ]A ′ + M[ u u ′ ] .

244

M[yy′] есть не что иное, как ковариационная матрица Cy общих

факторов, а M[u u ′] ковариационная матрица V характерных факторов. Таким образом,

Согласно предпосылкам факторного анализа Cy есть единичная

Соотношение (11.2) либо (11.2а) иногда называют фундаментальной теоремой факторного анализа. Она утверждает, что ковариационная матрица исходных признаков может быть воспроизведена с помощью матрицы факторных нагрузок и дисперсионной матрицы характерных факторов.

На практике обычно используют не ковариационную Cx , а кор-

реляционную матрицу R исходных признаков. Переход от ковариационной к корреляционной матрице означает, что исходные центрированные переменные подвергаются нормированию делением значений каждого признака на среднее квадратическое отклонение этого признака. Такое преобразование позволяет избежать влияния масштаба измерения на результаты анализа. Преобразованные признаки будут иметь, очевидно, единичную дисперсию, их ковариа-

ционная матрица совпадает с корреляционной, а соотношение (11.2) примет вид:

где В и W имеют тот же смысл, что A и V, но для нормированных признаков.

Для диагональных элементов матрицы R выполняется соотношение:

245

Общность указывает ту долю единичной дисперсии исходного признака, которую можно приписать общим факторам. Часть единичной дисперсии, которая не связана с общими факторами, назы-

вают характерностью wi2 :

Характерность иногда разбивают на две составляющих, одна из которых, gi2 , называется специфичностью, а другая, ei2 , является

дисперсией, обусловленной ошибкой, т.е. wi2 gi2 ei2 .

Факторное изображение допускает геометрическую интерпретацию. Согласно (11.1) точка в n-мерном пространстве исходных признаков представляется в виде линейной комбинации в (m+n)- мерном пространстве общих и характерных факторов, называемом также полным факторным пространством. Так как нагрузки общих факторов однозначно определяют дисперсии характерных факторов, то достаточно представлять признаки в m-мерном ортогональном пространстве общих факторов. Поскольку пространство общих факторов имеет размерность на n меньшую размерности полного факторного пространства, в факторном анализе используют обычно пространство общих факторов.

Весьма информативным является представление матрицы В в пространстве общих факторов в виде точек с координатами, соответствующими строкам В, т.е. координаты i-й точки есть

bi1 ,bi 2 ,...,bim . Соединяя эти точки с началом координат, получаем n

векторов-признаков. Длина вектора, отвечающего i-му признаку, равняется, как видно из (11.4), корню квадратному из общности.

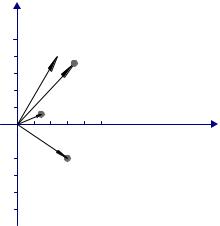
На рис. 11.1 в качестве примера приведена графическая иллюстрация факторного отображения пяти исходных переменных в пространстве двух исходных факторов. Числа 1,2,…,5 около точек соответствуют номерам строк матрицы В, иначе номерам исходных признаков.

246

Рис.11.1. Графическая иллюстрация факторного отображения

11.2. Этапы факторного анализа

Вычислительный аспект факторного анализа связан с определением факторного отображения В, дисперсий характерных факторов и оценкой значений общих факторов. Оценка этих параметров производится на основании экспериментальных данных, полученных в ходе наблюдений над N объектами (индивидами). Результаты наблюдений представляются в виде матрицы исходных данных, аналогичной (11.1). По матрице Х вычисляется корреляционная матрица R. Затем начинаются этапы собственно факторного анализа. Первый этап – оценка общностей. Если общности оценены, то по формуле (11.5) можно оценить характерности, а следовательно, и матрицу W, которая является диагональной согласно предпосылкам факторного анализа. Заменяя диагональные элементы матрицы R на оценки общностей, получают матрицу Rh , которая является

информационной основой второго этапа выделения факторов. На этом этапе решают тем или иным способом матричное уравнение

247

AA Rh , получая в итоге ортогональную матрицу A. Возможно большое число матриц A, которые одинаково хорошо будут воспроизводить матрицу Rh . Из них должна быть выбрана одна, что

составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, изза большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.

Выделение факторов. Выделение факторов предполагает установление числа и направления осей координат, соответствующих общим факторам. С алгебраической точки зрения проблема факторов означает определение ранга матрицы А и оценивание ее элементов. Для решения задачи выделения факторов разработано достаточно много методов, однако основными в настоящее время следует признать два: метод главных факторов, наиболее широко употребляемый на практике, и метод максимального правдоподобия, имеющий прочный математико-статистический фундамент.

Метод главных факторов. Как следует из фундаментальной теоремы факторного анализа (11.3), R W BB . Приравняем вначале W нулевой матрице. Получим матричное уравнение

Матричное уравнение (11.6) имеет множество решений: любое ортогональное преобразование Т, переводящее матрицу В в G, т.е. G = ВТ, удовлетворяет (11.6). Действительно, в силу ортогональ-

ности Т имеет место T 1 T и, значит, B GT . Подставляя выражение для В в (11.6), получаем

R GT GT GT TG GG ,

поскольку T′T=I.

Как известно из линейной алгебры, ортогональное преобразование системы координат означает поворот системы как целого на некоторый угол вокруг начала координат. Выделяя некоторое предпочтительное направление и фиксируя тем самым угол поворота

248

системы координат, можно обойти проблему неоднозначности решения системы (11.6).

Вернемся на время к методу главных компонент. Выбор осей координат здесь подчинен определенному требованию: каждая следующая ось ориентирована по направлению максимальной дисперсии в пространстве, ортогональном предыдущим главным компонентам. Матрица весовых коэффициентов А при этом составлена из собственных векторов ковариационной (корреляционной R) матри-

равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем от A к Q A 12 . Выражение для R примет

Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы В можно взять матрицу

Q A 12 .

Таким образом, матрица факторных нагрузок получается из матрицы, составленной из собственных векторов корреляционной матрицы исходных признаков, с последующим умножением элементов собственного вектора, отвечающего i-му собственному значению λi

на λi , i 1,2,...,n .

Матрицы B и Q имеют разный порядок: n m у В и n n у Q, поэтому правильнее говорить, что оценкой будут первые m столбцов матрицы Q.

Посчитав матрицу W равной нулю, мы для оценки матрицы B воспользовались моделью главных компонент. Строго говоря, под

249

методом главных факторов понимают способ расчета, принятый в методе главных компонент, но примененный к матрице Rh (оценка

общностей рассматривается ниже).

0ценка числа общих факторов. Общепризнанного метода оп-

ределения числа m общих факторов, подлежащих выделению, не существует. Однако разработан ряд критериев, с помощью которых можно сделать достаточно обоснованное заключение.

Широкое применение получил сравнительно простой критерий собственных значений: выделять только те факторы, которые соответствуют собственным значениям, большим единицы.

Рассмотрим матрицу Q Q .Справедлива следующая цепочка равенств:

Q Q ( A 12 ) A 12 12 A A 12 .

Полученное соотношение показывает, что сумма квадратов нагрузок i-го общего фактора на исходные признаки равняется i-му собственному значению i . Но i характеризует вклад i-го общего фактора в полную дисперсию (напомним, что полная дисперсия равняется следу корреляционной матрицы R и trR tr ). Поэтому факторы, вклады которых меньше единицы, имеют долю дисперсии, меньшую единичной дисперсии исходных признаков, и их нецелесообразно включать в число общих факторов.

Считается также, что вклад общих факторов в суммарную общность должен составлять около 90 %, а число общих факторов не должно превышать половины числа исходных признаков, т.е.

m < n /2, а более точно, (n m) (n m)2 .

К проблеме оценки числа факторов можно подойти со статистической точки зрения. Ранее отмечалось, что если коэффициенты корреляции после учета m факторов незначимо отличаются от нуля, то нет необходимости вводить (m+1)-й фактор. Другими словами, равенство C BmBm должно выполняться в статистическом смысле (здесь Bm − матрица факторных нагрузок с числом факторов, равным m). Для оценки значимости матрицы R (в самом нача-

250