Назаметдинов Анализ данных 2012

няются во времени. Случайный процесс Y(t) называется стацио-

нарным, если для любых n, t1,t2,…,tn распределения случайных ве-

личин (X(t1),X(t2), . . . , X(tn)) и (X(t1+τ),X(t2+τ), . . . , X(tn+τ)) одинако-

вы. Иными словами, функции конечномерных распределений не меняются при сдвиге времени:

Образующие стационарную последовательность случайные величины распределены одинаково, так что определенный выше процесс белого шума является стационарным.

7.7. Проверка ряда на случайность

Простейшей гипотезой, которую можно выдвинуть относительно колеблющегося ряда, не имеющего явно выраженного тренда, является предположение, что колебания случайны. В случайных рядах, согласно гипотезе, наблюдения независимы и могут следовать в любом порядке. Рассмотрим вначале непараметрические критерии [13], не требующие каких-либо ограничений на вид распределения совокупности.

1. Критерий поворотных точек состоит в подсчёте числа

«пиков» (величин, которые больше двух соседних y t - 1 < y t > y t + 1 ) и «впадин» (величин, которые меньше двух соседних y t - 1 > y t < y t + 1 ). Для определения поворотной точки требуются три последовательных значения. Начальное и конечное значения не могут быть поворотными точками, так как неизвестны y0 и yN+1. Если ряд случаен, то эти три значения могут следовать в любом из шести возможных порядков с равной вероятностью. Только в четырёх из них будет поворотная точка, а именно, когда наибольшее или наименьшее из трёх значений находится в середине. Следовательно, вероятность обнаружения поворотной точки в любой группе из трёх значений равна 2/3.

Для последовательности из N величин определим счётную переменную xi:

161

N 1

Тогда число поворотных точек р есть p xt , а их математи-

t 2

ческое ожидание есть М p = 23 (N-2). Дисперсия числа поворотных

точек вычисляется по формуле [13] D p =(16N-29)/90, само распределение близко к нормальному.

Проиллюстрируем применение описанного критерия на примере ряда среднесуточных температур февраля 2001 года (табл. 7.1).

Таблица 7.1

Исходный ряд содержит 28 наблюдений, однако в четырех местах подряд идут одинаковые значения, создавая зону неопределенности. В таких ситуациях в ряде сохраняют только одну точку. Длина ряда при расчете критериев уменьшается на число отброшенных значений (в примере 4, так что N=24). Пиками в исследуемом ряде будут значения при t=4,8,10,13,16, 23; впадинами – значения при t=3,5,9,12,14,20,26. Всего поворотных точек в ряде 13

(р=13), Для случайного ряда Mp 23 (24 2) 14,66 ; Dp=3,94. Ин-

тервальное значение числа поворотных точек при уровне надежно-

ченный интервал накрывает точку р=13, что не противоречит гипотезе о случайности ряда температур.

2. Критерий, основанный на определении длины фазы. Под

фазой понимают интервал между двумя ближайшими поворотными точками. Фаза называется восходящей, если начинается с «впадины», и нисходящей, если начинается с «пика». Фаза (для опреде-

162

когда y t > y t + i , i = 1,2,…, N-t. Всего для сравнения имеется N(N-1)/2 пар. Пусть – общее число случаев превышения. Подсчитывают

этот коэффициент значим и отрицателен, то ряд возрастающий, если положителен, то – убывающий.

В случае нормальных возмущений проверку на случайность проводят с помощью автокорреляционной функции, значения которой не должны значимо отклоняться от нуля (подробнее см. п. 7.9).

Нестационарность в моделях типа авторегрессии обсуждается также в п. 7.10.4.

7.8. Числовые характеристики случайной составляющей

При анализе временных рядов используются числовые характеристики, аналогичные характеристикам случайных величин:

математическое ожидание m(t)=M[X(t)]; автоковариационная функция

B(s,t) cov(X (t), X (s)) M (X (t) m(t))(X (s) m(s)) ;

дисперсия D(t) = B(t,t) = cov(X(t),X(t));

стандартное отклонение σ(t) 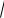D(t) ;

автокорреляционная функция; частная автокорреляционная функция.

Случайность во временных рядах имеет двоякую природу: в каждый момент времени t предполагается возможность множества реализаций, т.е. X(t) рассматривается просто как случайная величина. С другой стороны, последовательные значения случайной величины X(t) при t =1,2,…,N в конкретном случае, иначе при определенных (сложивштхся) условиях, образуют реализацию случайного процесса. Так, в операторе M[ X (t)] усреднение про-

исходит при неизменном t, т.е. математическое ожидание берется по множеству реализаций. Рассмотрим введенные числовые характеристики для стационарных процессов. Из определения стационарности следует, что для любых s, t и τ

m(t τ) m(t), (t τ) (t), R(s τ,t τ) R(s,t).

164

Положив τ = –t, получаем:

m(t) m(0), σ(t) σ(0), B(s, t) B(s t,0), R(s, t) R(s t,0). (7.15)

Выходит, у стационарного процесса математическое ожидание и дисперсия одинаковы при любом t, а автоковариационная и автокорреляционная функции зависят не от момента времени s или t, а лишь от их разности (лага).

Отметим, что выполнение свойств (7.15) еще не влечет стационарности в смысле определения (7.14). Тем не менее постоянство первых двух моментов, а также зависимость автокорреляционной функции только от лага определенно отражает некоторую неизменность процесса во времени. Если выполнены условия (7.15), то говорят о стационарности процесса в широком (нестрогом) смысле, тогда как выполнение условий (7.14) означает стационарность в узком (строгом) смысле.

Данное выше определение белого шума надо трактовать в узком смысле. На практике часто ограничиваются белым шумом в широком смысле, под которым понимают временной ряд (случайный процесс), у которого

Отметим, что гауссовский процесс, стационарный в узком смысле, стационарен и в широком смысле.

7.9. Оценивание числовых характеристик временного ряда

Оценивание числовых характеристик случайного временного ряда в каждый момент времени требует набора реализаций (траекторий) соответствующего случайного процесса. Хотя время и не воспроизводимо, однако условия протекания процесса иногда можно считать повторяющимися. Особенно это характерно для технических приложений, например, колебания напряжения в электрической сети в течение суток. Временные ряды, наблюдаемые в разные сутки, можно считать независимыми реализациями одного случайного процесса.

165

Иная ситуация при исследовании процессов социальноэкономической природы. Как правило, здесь доступна единственная реализация процесса, повторить которую не представляется возможным. Следовательно, получить оценки среднего, дисперсии, ковариации нельзя. Однако для стационарных процессов подобные оценки все-таки возможны при условии эргодичности процесса. Стационарный (в слабом смысле) процесс yt с My t = m и одинако-

вой дисперсией M( yt m)2 σ2 при всех t обладает свойством эргодичности (по отношению к средней), если средняя по времени

y 1 N yt сходится по вероятности к m при N→∞.

N t 1

но, и эргодичность процесса, устанавливается теоремой Слуцкого, которая требует, чтобы

1 N 1

N t 1 rt 0 , при N → , где rt – автокорреляционная функция процесса.

Приведенное условие является необходимым и достаточным. Точность оценивания среднего зависит от длины N ряда. Счита-

ется, что длина N всегда должна быть заведомо больше так называемого времени корреляции, под которым понимают величину

T = rk . Величина Т дает представление о порядке величины

k 1

промежутка времени , на котором сохраняется заметная корреляция между двумя значениями ряда.

166

Эти пары можно рассматривать как выборку двух случайных величин, для которых можно определить оценку стандартного ко-

rˆk объем выборки меняется, меняется значение среднего и стан-

дартного отклонения для соответствующего набора значений. Для упрощения принято центрировать наблюдения относительно сред-

него значения всего ряда ~ ~ ~ и заменять дисперсионные y1, y2 ,..., yN

члены в знаменателе на дисперсию ряда в целом, т.е.

лагов m = max k не превышает четверти длины ряда (m ≤ N/4). Если ряд рассматривается как генеральная совокупность беско-

нечной длины, то говорят об автокорреляциях (теоретических) и обозначают их rk. Массив коэффициентов r1, r2 ,… или соответ-

весьма ценную информацию о внутренней структуре ряда. Совокупность коэффициентов корреляции, нанесенная на график с координатами k (лаг) по оси абсцисс и rk либо rˆk по оси ординат,

называют коррелограммой (теоретической или выборочной соответственно).

Точностные характеристики оценки rˆk получены для гауссовских процессов [13]. В частности, для гауссовского белого шума, у которого все корреляции равны нулю, D[rˆk ] 1/ N . Математическое ожидание rk для гауссовского белого шума оказывается не

равным нулю, а именно, M[rˆk ] N1 , т.е. оценка rˆk оказывается

смещенной. Величина смещения убывает с ростом N и не столь существенна в прикладном анализе.

167

7.10. Теоретический анализ стационарной случайной составляющей линейного вида

Общая линейная модель стохастического процесса есть:

Введем оператор сдвига В на один шаг назад: Bεt εt 1. Многократное (для определенности j-кратное) применения опе-

где C(B) 1 c1B c2 B2 ...– линейный оператор.

Найдем математическое ожидание, дисперсию и автоковариационную функцию для процесса (7.16):

j 0

169

Кроме этого, предполагают, что имеет место так называемое условие обратимости:

где вместо В фигурируют комплексные числа. Из этого условия вытекает существование обратного оператора

Раскрывая произведение в последнем выражении, группируя однородные по B j члены и приравнивая их к нулю, получают вы-

Запись (7.20) соответствует авторегрессионой схеме бесконечного порядка. Это же соотношение можно трактовать как линейный предиктор по всем прошлым значениям временного ряда, а

слагаемое εt – как случайную ошибку этого предиктора. Если из-

вестны все прошлые значения ряда, то по формуле (7.20) можно спрогнозировать будущее значение ряда.

7.10.1. Модели авторегрессии

Рассмотрим более подробно модели случайной составляющей, являющиеся частными случаями общей линейной модели, а именно: модели авторегрессии, скользящего среднего и смешанные, широко применяемые на практике.

Авторегрессия первого порядка (марковский процесс).

170