Назаметдинов Анализ данных 2012

f (x1)(F F ) 1 f (x1) max f (x1 )(F F ) 1 f (x1 ) .

* 0 0 * x1 0 0

Координаты найденной точки x*1 подсоединяют к матрице Х0, образуя новый план Х1 с информационной матрицей

F1F1 F0 F0 f (x*1) f (x*1) .

На последующих шагах поступают аналогично, пополняя матрицу плана Х все новыми точками. После некоторого количества итераций матрицу Х нормируют, получая непрерывный план l. Данная процедура приводит к непрерывному D-оптимальному плану.

Не исключено, что в ходе расчетов могут появиться точки с очень малыми частотами либо с очень близкими координатами. В таких случаях подобные точки отбрасывают либо объединяют в одну. В качестве меры близости получившегося после m итераций плана к D-оптимальному естественно взять

6.2. Методы экспериментальной оптимизации

Технические, а в основном экономические причины заставляют стремиться к тому, чтобы управление объектом (процессом) обеспечивало протекание его в оптимальных условиях. При этом достигается наиболее полное соответствие между затрачиваемыми ресурсами и выходным результатом. Часто требуется, чтобы продукция обладала оптимальными свойствами, например, имела наибольшую прочность, чистоту и т.п.

Для нахождения оптимума выбранной целевой величины возможны два подхода. Первый предполагает построение экспе- риментально-статистической модели с последующим поиском оптимальной области аналитическими методами. Хотя знание модели во всей области представляет несомненный интерес, для задачи оптимизации эта информация в известной мере избыточна. Действительно, исследователю интересен лишь малый фрагмент области – тот, где находится экстремум. Учитывая также затраты на построение модели во всей области, использование первого под-

121

В зависимости от вида функции поиск прекращается при раз-

личных i, так что средняя эффективность составит

E =( N – 1)/ 2 .

Метод деления отрезка пополам

Эксперименты ставят парами в точках, отстоящих по обе стороны от середины отрезка. Координаты первой пары:

x1 (b a) / 2 ε , x2 (b a) / 2 ε,

где – малая величина.

Если f (x1) f (x2 ) , то максимальное значение надо ожидать на отрезке [a, x2 ]; при f (x1) f (x2 ) на отрезке [x1, b] . Этот новый отрезок объявляется исходным, и далее процесс повторяется. Мера

эффективности равна E 2N 2 .

Заметим, что при наличии случайного компонента значение не должно быть малым, что иллюстрируется рис.6.1.

Если в точке х1 случайный компонент окажется отрицательным, а в точке х2 положительным и значительным по величине в обеих точках, результаты сравнения значений отклика в этих точках направят поиск в противоположную сторону. Вот почему применение метода деления отрезка пополам в этих условиях становится проблематичным.

у

Рис. 6.1. Метод деления отрезка пополам

123

Поиск с использованием чисел Фибоначчи

Числа Фибоначчи задаются по следующим правилам:

F0 F1 1, Fk Fk 2 Fk 1

На первом шаге ставятся два эксперимента в точках

x 1 = a + ( b - a ) q и x 2 = b - ( b - a ) q при q=F N - 2 / F N , (6.10)

где N выбирается заранее.

При f (x1) f (x2 ) максимальное значение следует искать на отрезке [a, x2 ] , при f (x1) f (x2 ) – на отрезке [x1,b] . На последующих шагах ставят по одному эксперименту, меняя q по закону

q j FN 1 j , где j – номер шага (j = 2, 3,…).

FN 1 j

Можно показать, опираясь на определение чисел Фибоначчи, что одна из координат, подсчитанная по формулам, аналогичным (6.10), будет совпадать с одной из предыдущих точек. Далее происходит сравнение значений функций в этих двух точках и процесс повторяется.

Мера эффективности метода составляет E FN .

Так, при N=11 FN =144, а значит с помощью 11 экспериментов

можно локализовать экстремум в области, не превышающей 1% размера начальной области поиска. Этот метод существенно эффективнее предыдущего. К его недостатку можно отнести необходимость заранее задавать число экспериментов.

Метод золотого сечения

Этот метод базируется на методе Фибоначчи и не требует предварительного задания числа экспериментов. В методе золотого се-

124

6.2.2. Многомерный поиск

Для поиска экстремума функции многих переменных применяется ряд методов, среди которых отметим:

метод покоординатной оптимизации; градиентные методы; последовательный симплексный метод.

Метод покоординатной оптимизации

Метод покоординатной оптимизации, называемый также методом Гаусса–Зейделя, сводит многомерную оптимизацию к последовательному применению одномерной к сечениям функции. Для этого фиксируют значения всех переменных, кроме одной, к которой применяется один из методов одномерной оптимизации. Затем начинают поиск по второй переменной, фиксируя первую на значении, обеспечившем экстремум, и т. д. После того как список переменных исчерпался, возвращаются к первой переменной, и так до тех пор, пока значение отклика возрастает (убывает). Метод отличается простотой, однако для функций овражистого типа, для которых линии равного уровня сильно вытянуты в направлении, не параллельном осям координат, поиск может продолжаться довольно долго.

Градиентные методы

Эти методы предполагают нахождение градиента в некотрой точке с последующим продвижением в направлении градиента по шагам. Если градиент пересчитывается на каждом шаге, то это собственно градиентный метод, если же движение в направлении градиента продолжается до тех пор пока целевая функция растет, то это метод крутого восхождения (в случае поиска минимума, гово-

рят о методе наискорейшего спуска).

Поиск начинается с некоторой начальной точки x0. На основе малой серии опытов строится линейное описание поверхности от-

125

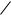
клика в окрестности x0. В центре этой локальной области определяется значение градиента, после чего начинаются опыты в направлении градиента. Бокс и Уилсон предложили использовать дробные факторные планы для поиска линейной модели. Метод состоит из последовательности циклов, каждый из которых содержит два шага.

1. Построение линейной модели в окрестности некоторой на-

чальной точки x* с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьи-

рования i 12 xi*max xi*min по отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели одинаковый порядок. В случае адекватности ли-

где i, j,…,k – направляющие векторы осей координат.

Обычно переходят к нормированному градиенту делением его

компонент на норму ( aˆi2 )12 либо просто на max aˆi . Компоненты

i

ˆ .

нормированного градиента обозначим bi , i 1,2,...n

2.Пошаговое увеличение величины целевой функции (движение

внаправлении градиента). Координаты точки наблюдения на k-м шаге при движении в направлении градиента определяются по

ющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной обла-

сти, тем меньше λ k . Движение в направлении градиента про-

должается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план,

126

находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям.

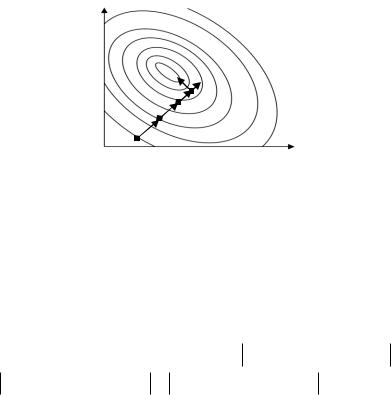
Геометрическая интерпретация метода приведена на рис.6.2. Здесь поверхность отклика задается линиями уровня.

x2

x1

Рис. 6.2. Схема метода Бокса–Уилсона

Рассмотрим в качестве примера использование метода Бокса−Уилсона для поиска максимума функции

1х3 15. Начальная точка поиска х0= (x10 , x20 , x30 ) = (3, 2, 4 ) . Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями: xi0 i xi xi0 i , i = 1,2,3. Значения i желательно подбирать такими, чтобы приращения функции по каждому аргументу были сопоставимы, т.е. y(x10 1, x20 , x30 ) y(x0 )

y(x10 , x20 2 , x30 ) y(x0 ) y(x10 , x20 , x30 3 ) y(x0 ) . Примем 1=

=1, 2=2, 3=3.

127

В соответствии с (6.1) стандартизованная переменная xi ст 1,

своей оценки не менее четырех экспериментов. Воспользуемся

В последнем столбце табл. 6.1 содержатся значения функции (6.11) для исходных переменных, т.е. 40,8= у (4,4,7) и так далее.

МНК-оценки коэффициентов линейной модели составят:

аˆ (40,8 26,2 24,4 25,4) / 4 3,4 ;

1

aˆ2 (40,8 26,2 24,4 25,4) / 4 4,3 ; aˆ3 (40,8 26,2 24,4 25,40 / 4 3,9 .

Отнормируем полученные компоненты градиента, поделив их на максимальное значение аˆ2 4,3 : b1=3,4/4,3=0,79, b2=1, b3=0,91.

Движение в направлении градиента представлено в табл.6.2.

128

Движение в направлении градиента после четвертого шага невозможно из-за ограничения на х3. Теперь следует определить градиент в точке x0+3bi i. Поскольку темп роста функции замедлился на последних шагах, область линейного описания следует сузить, уменьшив значения i.

6.2.3. Последовательный симплексный метод

Этот метод требует проведения минимально возможного числа опытов при определении направления движения.

Симплексом в n-мерном пространстве называют многогранник с (n+1)-й вершиной. Если расстояния между вершинами симплекса одинаковы, такой симплекс называют регулярным. Симплексный метод [28] включает в себя следующие основные процедуры:

1.Линейное преобразование входных переменных с таким расчетом, чтобы изменение каждой из них на единицу одинаково сказывалось на изменении выходной переменной.

2.Построение регулярного симплекса и реализация опытов в вершинах симплекса.

3.Отбрасывание вершины с минимальным значением целевой величины и построение нового симплекса, который образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой зеркальным отображением отброшенной вершины от-

носительно противоположной ей (n 1) -мерной грани исходного

симплекса. Координаты этой новой вершины рассчитываются по формуле:

xH n2 x(1) x(2) x( j 1) x( j 1) ... x(n 1) x( j) ,

где j − номер отброшенной вершины.

4. Проведение эксперимента в вершине xH и возврат к п. 3. Ес-

ли оказывается, что выходная переменная в новой вершине приняла значение меньшее, чем в остальных вершинах симплекса, то следует возвратиться к предыдущему симплексу. Во избежание зацикливания в качестве отбрасываемой выбирают вершину, в которой выходная переменная имеет величину, следующую по по-

129

рядку за наихудшей вершиной симплекса. Аналогично следует поступать, если новая вершина выходит за пределы симплекса.

5. Если при перемещении симплекса за n 1 шагов некоторая вершина сохраняет свое положение, то симплекс совершит оборот относительно этой вершины. Это означает достижение области оптимума. Другим условием достижения оптимума является выпол-

(порог), ycp – среднее значение выходной величины в вершинах

симплекса.

К числу достоинств симплексного метода наряду с экономичностью по числу опытов и простотой вычислений следует отнести также возрастание эффективности метода с ростом числа входных переменных, устойчивость выделения направления движения, поскольку оно определяется только соотношением целевых величин, а не их абсолютными значениями.

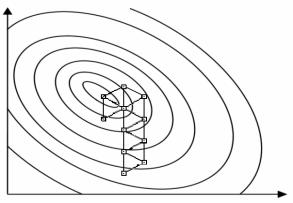
Графическая иллюстрация симплексного метода при двух входных переменных приведена на рис.6.3. Здесь поверхность отклика задается линиями уровня.

x2

x1

Рис. 6.3. Схема последовательного симплексного метода

130