Назаметдинов Анализ данных 2012

9.3. Функционалы качества разбиения на кластеры

Разбиение исходной совокупности объектов на кластеры может осуществляться различными способами. Естественно поэтому определить тот количественный критерий, следуя которому можно было бы предпочесть одно разбиение другому. С этой целью в постановку задачи кластерного анализа вводят понятие функционала качества разбиения G(К). Этот функционал определяется на мно-

жестве всех возможных разбиений. Разбиение K * , которое доставляет экстремум выбранному функционалу, считается наилучшим. Следует отметить, что выбор функционала, так же как и выбор метрики, осуществляется скорее на основе эмпирических и про- фессионально-интуитивных соображений, чем на какой-либо строгой формализованной системе.

Функционал качества разбиения должен отражать разнородность множества объектов. Пользуясь понятием расстояния, введем вначале меры рассеяния множества объектов, которые строятся на базе матрицы расстояний D (9.2). Величину Sd O , равную полу-

сумме всех элементов матрицы D, называют общим рассеянием, а

где ( Х Х ) – центрированная матрица исходных наблюдений, X – матрица, столбцы которой состоят из средних значений соответствующих переменных. След матрицы S X называют статистиче-

ским рассеянием множества О и обозначают

Из (9.4) видно, что S t (O ) равна сумме квадратов евклидовых расстояний точек от центра тяжести. Величину S t ( O ) часто назы-

вают также внутрикластерной дисперсией.

211

Пользуясь введенными мерами рассеяния, определим функционалы качества разбиения. Пусть K = {K1,K2,…,Km} – некоторое фиксированное разбиение наблюдений X1,X2, …,XN на заданное число m клаcтеров K1,K2,…,Km. В качестве функционалов качества часто берутся следующие характеристики:

1) сумма общих

(n=1); результаты измерений сведены в матрицу (для данного примера – вектор) Х={3,4,7,4,3,3,4,4} . Очевидно, X 328 4 . Сумма

квадратов отклонений для исходного множества О составит

8

G3 O ( X i X )2 ( 1)2 3 0 4 32 12.

i 1 ,

Если множество O разбить на три группы K1 O1 ,O5 ,O6

K2 O2 ,O4 ,O7 ,O8 , K3 O3 , то внутригрупповые суммы квад-

ратов будут равны нулю, так что

G3 (K) G3 (K1) G3 (K2 ) G3 (K3 ) 0 .

Полученное разбиение при числе групп, равное трем, будет, очевидно, оптимальным, поскольку функционал G3 является неотрицательной величиной.

212

Описанные выше функционалы пригодны тогда, когда число кластеров известно заранее. В ситуациях, когда это число заранее неизвестно, в функционал качества разбиения вводят составляющую, которая является возрастающей функцией числа кластеров. Эта составляющая может интерпретироваться как некоторая мера взаимной удаленности кластеров, либо как мера тех потерь, которые возникают при излишней детализации массива исходных наблюдений. Возможны и другие интерпретации. Приведем весьма простой функционал качества разбиения

G4 (K) I1(K) I2 (K) ,

где I1(K ) − суммарное внутрикластерное рассеяние (в качестве которого могут выступать функционалы G1,G2 ,G3 ), I2 (K ) – линейно возрастающая функция числа кластеров.

9.4. Алгоритмы раздельной кластеризации

Задача кластерного анализа носит комбинаторный характер. Прямой способ решения такой задачи заключается в полном переборе всех возможных разбиений на кластеры и выбора разбиения, обеспечивающего экстремальное значение функционала. Такой способ решения называют кластеризацией полным перебором. Аналогом кластерной проблемы комбинаторной математики является задача разбиения множества из n объектов на m подмножеств. Число таких разбиений обозначается через S(n,m) и называется числом Стирлинга второго рода. Эти числа подчиняются рекуррентному соотношению:

S(n 1,i) iS(n,i) S(n,i 1) .

При больших n

S n, m mn 1 .

Из этих оценок видно, что кластеризация полным перебором возможна в тех случаях, когда число объектов и кластеров невелико.

К решению задачи кластерного анализа могут быть применены методы математического программирования, в частности, динамического программирования. Хотя эти методы, как и полный пере-

213

бор, приводят к оптимальному решению в классе всех разбиений, для задач практической размерности они не используются, поскольку требуют значительных вычислительных ресурсов. Ниже рассматриваются алгоритмы кластеризации, которые обеспечивают получение оптимального решения в классе, меньшем класса всех возможных разбиений. Получающееся локально-оптимальное решение не обязательно будет оптимальным в классе всех разбиений.

Наиболее широкое применение получили алгоритмы последовательной кластеризации. В этих алгоритмах производится последовательный выбор точек-наблюдений и для каждой из них решается вопрос, к какому из m кластеров ее отнести. Эти алгоритмы не требуют памяти для хранения матрицы расстояний для всех пар объектов.

Остановимся на наиболее известной и изученной последовательной кластер-процедуре – методе k-средних (k-means). Особенность этого алгоритма в том, что он носит двухэтапный характер: на первом этапе в пространстве Еn ищутся точки – центры клacтеров, а затем уже наблюдения распределяются по тем кластерам, к центрам которых они тяготеют. Алгоритм работает в предположении, что число m кластеров известно.

Первый этап начинается с отбора m объектов, которые принимаются в качестве нулевого приближения центров кластеризации. Это могут быть первые m из списка объектов, случайно отобранные m объектов, либо m попарно наиболее удаленных объектов.

Каждому центру приписывается единичный вес. На первом шаге алгоритма извлекается первая из оставшихся точек (пометим ее

как x m 1 ) и выясняется, к какому из центров она оказалась ближе всего в смысле выбранной метрики d. Этот центр заменяется новым, определяемым как взвешенная комбинация старого центра и новой точки. Вес центра увеличивается на единицу. Обозначим че-

рез Zi n-мерный вектор координат i-го центра на v-м шаге, а через

pi – вес этого центра. Пересчет координат центров и весов на -м

шаге при извлечении очередной точки осуществляется следующим образом:

214

При достаточно большом числе классифицируемых объектов имеет место сходимость векторов координат центров кластеризации к некоторому пределу, т.е., начиная с некоторого шага, пересчет координат центров практически не приводит к их изменению.

Если в конкретной задаче устойчивость не имеет места, то производят многократное повторение алгоритма, выбирая в качестве начального приближения различные комбинации из m точек.

После того как центры кластеризации найдены, производится

окончательное распределение объектов по кластерам: каждую точку xi, i =1,2,…, N относят к тому кластеру, расстояние до центра

которого минимально.

На рис.9.2 приводится иллюстрация первого этапа работы алгоритма. Здесь в качестве начальных центров кластера взяты первые два исходных объекта. Обратите внимание, что отрезок, соединяющий центр с очередным объектом, делится согласно (9.5) в соотношении р:(р+1), где р – число объектов в кластере.

Как видно из рисунка, объекты О1,О2,О3 войдут в один кластер, поскольку они ближе (в смысле евклидова расстояния) к центру Z1, О4,О5 составят второй кластер, поскольку близки к Z2′′′.

Описанный алгоритм допускает обобщение на случай решения задач, для которых число кластеров заранее неизвестно. Для этого задаются двумя константами, одна из которых Ф0 называется мерой грубости, а вторая Ψ0 – мерой точности.

215

Число центров кластеризации полагается произвольным (пусть m0 ), а за нулевое приближение центров кластеризации выбирают произвольные m0 точек. Затем производится огрубление центров заменой двух ближайших центров одним, если расстояние между ними окажется меньше порога Ф0 . Процедура огрубления заканчивается, когда расстояние между любыми центрами будет не меньше Ф0 . Для оставшихся точек отыскивается ближайший центр кластеризации, и если расстояние между очередной точкой и ближайшим центром окажется больше, чем Ψ0, то эта точка объявляется центром нового кластера. В противном случае точка приписывается существующему кластеру, координаты центра которого пересчитываются по правилам, аналогичным (9.5), (9.6).

9.5. Иерархический кластерный анализ

Наряду с обычным, «раздельным», кластерным анализом широко применяется иерархический кластерный анализ, цель которого состоит в получении всей иерархии разбиений, а не отдельного разбиения. Считается, что иерархия точнее характеризует размытую структуру данных, чем отдельное разбиение. Получить конкретное разбиение в случае необходимости сравнительно легко сечением графа иерархий.

216

9.5.1. Основные определения

Пусть О = {O1, O2, …,ON} – конечное множество объектов. Иерархией h на О называется система подмножеств (классов) {K: K O}такая, что

1)O h;

2){Oi} h, i=1,2,…,N;

3)для пересекающихся подмножества K и K´, т.е. K K´ ≠ Ø,

K K´ либо K´ K.

Пример. Пусть О = {О1, О2,…, О5}. Тогда система подмножеств h = {{O1}, {O2}, …,{O5}, {O1,O2}, {O3,O4}, {O1,O2,O5}, O}

является иерархией на О.

Иерархия может быть представлена на языке теории графов. Графом иерархии h на О называется ориентированный граф (V,E), вершины v V которого соответствуют множествам K h , а ребра e E – парам (K´,K), таким что K´ K. Ребро e = (K´,K) изображается стрелкой с началом K´ и концом K.

Иерархической классификацией данного множества объектов

О = {O1, O2, …,ON} называется построение иерархии h на О, отражающей наличие однородных в определенном смысле классов.

Если использовать неориентированный граф, то его структура становится деревом. Сам процесс классификации есть построение иерархического дерева исследуемой совокупности объектов. Графическое изображение неориентированного графа иерархии на плоскости называют дендрограммой.

В иерархическом кластерном анализе используются два вида алгоритмов: дивизимные и агломеративные. В дивизимных алгоритмах множество О постепенно делится на все более мелкие подмножества, в агломеративных – наоборот: точки множества О постепенно объединяются во все более крупные подмножества. Соответственно, графы иерархий, полученные при помощи этих алгоритмов, называют дивизимными и агломеративными. Дивизимные алгоритмы называют также нисходящими (движение против стрелок на графе иерархии), агломеративные – восходящими (движение вдоль стрелок). Если на каждом шаге такого алгоритма объ-

217

единяются только два кластера, то говорят о бинарном агломеративном алгоритме. Далее рассматриваются лишь такие алгоритмы.

Более подробно схема работы бинарного агломеративного алгоритма выглядит следующим образом. Исходное множество объектов О = {O1, O2, …,ON} рассматривается как множество одноэлементных кластеров; выбирают два из них, например Ki и Kj, которые наиболее близки в смысле введенной метрики друг другу и объединяют их в один кластер. Новое множество кластеров будет

иметь уже N-1 элемент

K1,K2,…,{Ki,Kj},…,KN..

Рассматривая полученное множество в качестве исходного и повторяя процесс, получают последовательные множества кластеров, состоящие из N-2, N-3 и т.д. кластеров.

К достоинствам иерархических процедур относят полноту анализа структуры исследуемого множества наблюдений, возможность наглядной интерпретации проведенного анализа, возможность остановки процедуры при достижении априори заданного числа кластеров. К cущественным недостаткам иерархических процедур следует отнести финальную неоптимальность. Как правило, даже подчиняя каждый шаг работы процедуры некоторому критерию качества разбиения, получающееся в итоге разбиение для любого наперед заданного числа кластеров оказывается весьма далеким в смысле того же самого критерия качества.

9.5.2. Графическое представление результатов иерархической классификации

Иерархическая классификация, как уже отмечалось, допускает наглядную интерпретацию. Для того чтобы привязать граф иерархии или дендрограмму к системе прямоугольных координат, введем понятие индексации [2]. Индексацией иерархии называется отображение : h R1, ставящее в соответствие множеству K h число (K) R1 таким образом, что

1)(K) = 0 для одноэлементных множеств K, т.е. K = 1;

218

2) (K´) < (K) для каждой пары (K´,K) такой, что K´ K, K´≠ K.

Индексация иерархии позволяет алгоритмизировать процесс построения дендрограммы. Пусть (h,ν) – некоторая индексированная иерархия h на множестве О = {O1, O2, …,ON}. Вершины графа иерархии, отвечающие одноэлементным множествам {Oi}, i = 1,2, …, N, обозначим через νi, а вершины, соответствующие К (К > 1), обозначим νК. Введем систему координат с осью абсцисс х и осью ординат η. Вначале на оси х через равные интервалы размещают-

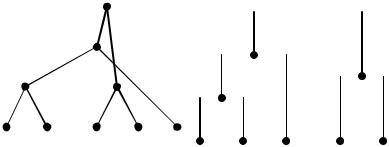
построенная таким образом дендрограмма может содержать нежелательные пересечения ребер, поэтому вершины переупорядочиваются так, чтобы ребра соединялись только в вершинах. На рис.9.3 представлены дендрограммы иерархии с пересечением и без. Заметим также, что традиционно ребра диаграммы изображают в виде вертикальных и горизонтальных отрезков, как на дендрограмме без пересечений (рис.9.3,б).

Способы задания индекса ν могут быть разные. Весьма распространена индексация, ставящая в соответствие множеству K h номер шага, на котором это множество было включено в иерархию. В качестве альтернативы индексом может выступать мощность множества, точнее ν = K -1.

219

Рис.9.3. Дендрограммы иерархии примера из п.9.5.1: а) − с пересечением ребер; б) − без пересечения ребер

Информативность дендрограммы существенно возрастает, если в качестве ординаты кластера K, полученного объединением кластеров Ki и Kj, т.е. K = Ki Kj, выступает расстояние между кластерами d(Ki, Kj). Такое изображение называют оцифрованным.

Одна из проблем иерархического кластерного анализа – определить, какие метрики позволяют провести оцифрование, удовлетворяющее условиям индексации, или иначе, найти индексацию, такую что ν (К i К j ) = d ( К i , К j ). Так, для евклидовой метрики ответ на этот вопрос – отрицательный, что можно проиллюстрировать следующим примером. Пусть пять двумерных объектов, под-

лежащих кластеризации, образуют конфигурацию, представленную на рис.9.4,а.

На первом шаге агломеративной процедуры получаем кластер К1=.{О1, О2} c координатами центра тяжести Z(К1) = (1,5;1). Для кластера К1, полученного объединением одноэлементных кластеров {O1} и {O2}, d(О1, О2) = 1. Ближайшим к К1 окажется объект О3 (точнее одноэлементный кластер К2={O3}) с координатами центра тяжести v(К2)= (1,5; ε ). На следующем шаге алгоритма образуется,

очевидно, кластер К3=К1 К2 с d(К1, К2) = (1 – ε )2, поскольку расстояние между кластерами измеряется по центрам тяжести (квадрат евклидова расстояния). Выходит для кластера К3 потенциаль-

220