Назаметдинов Анализ данных 2012

Как уже отмечалось, препятствием для применения обычного МНК является коррелированность y2t ,..., ymt с u1t . Однако если очи-

стить y2t ,..., ymt от случайной составляющей, применение МНК будет возможным. Поскольку случайная составляющая в отдельной точке t ненаблюдаема, можно получить ее оценку как разность ( yit – yˆit ) между наблюденным значением yit и оцененным yˆit . Если теперь из исходных наблюдений вычесть оценку случайной компо-

на все предопределенные переменные системы, после чего наблю-

система нормальных уравнений имеет вид:

202

Систему (8.10) можно записать в альтернативной форме, содержащей только реальные наблюдения.

Доказано, что оценки 2МНК состоятельны [5]. Кроме 2МНК, в котором каждое уравнение оценивается по отдельности, предложен трехшаговый МНК (3МНК). Здесь производится оценка всех уравнений системы с учетом их взаимодействия, что приводит вообщето к повышению эффективности оценок.

Вопросы и упражнения

1. Почему применение обыкновенного МНК для процессов случайного блуждания некорректно?

2.Что понимают под коинтегрируемостью временных рядов?

3.Какая форма СОУ является первичной?

4.Какие переменные называются предопределенными?

5.В чем состоит проблема идентифицируемости СОУ?

6.Получите приведенную форму для следующей СОУ:

y1t 3y3t 2x1t 4x3t 7x4t u1t ; y2t 2 y3t 3x2t x4t u2t ;

y3t 4 y1t 2 y2t 6x2t 3x3t u3t .

7.Как решается проблема коррелированности возмущений и переменных в 2МНК?

8.Как соотносятся число эндогенных переменных и число уравнений СОУ?

203

9. КЛАСТЕРНЫЙ АНАЛИЗ

Один из фундаментальных процессов в науке – классификация. Факты и явления должны быть упорядочены, классифицированы, прежде чем исследователь может понять их. К настоящему времени анализ данных располагает большим арсеналом методов классификации, систематизация которых может проводиться по разным основаниям. В теории и практике классификации можно выделить три класса задач: 1) кластеризации (кластерный анализ; близкие термины: автоматическая классификация без учителя, таксономия), 2) дискриминации (дискриминантный анализ; близкие термины: диагностика, автоматическая классификация с учителем), 3) группирование.

Кластерный анализ ставит своей целью выделение групп («скоплений», кластеров) сходных объектов; иными словами, ищется «естественное» разделение выборки на изолированные группы однородных объектов.

Вдискриминантном анализе отдельные группы задаются обучающими выборками и требуется вновь поступающий объект отнести к той или иной группе.

Вгруппировании также выделяются подмножества объектов, однако наличие кластеров в исходной выборке не требуется. Данные подмножества формируются исследователем обычно заданием границ.

Вданной главе мы ограничимся кластерным анализом.

Целями кластеризации являются:

1.Понимание данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа.

2.Сжатие данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера.

3.Обнаружение новизны (англ. novelty detection). Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.

204

9.1. Задача кластерного анализа

Имеется множество О = {О1,О2, …,ОΝ}, состоящее из N объек-

ров-строк, в n-мерном евклидовом пространстве En .

Пусть m − целое число, меньшее N. Задачу раздельного кластерного анализа (слово раздельный обычно опускают) можно сформулировать следующим образом: на основании данных, содержащихся в Х, разбить множество объектов О на m кластеров (подмножеств) К1,К2, …, КN так, чтобы каждый объект принадлежал одному и только одному подмножеству, т.е.

K1 K2 ... Km O, Ki K j , для всех i, j ; i ≠ j,

и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными (близкими), тогда как объекты, принадлежащие разным кластерам, были несходными (далекими).

Решение задачи кластерного анализа требует формализации понятий близости и различия. Рассмотрим понятие расстояния между

точками xi и x j из En .

9.2. Функции расстояния и сходства

Неотрицательная вещественная функция d (x i , x j ) называется функцией расстояния (метрикой), если:

а) d (x i , x j ) 0 для всех xi и xj из En ;

205

б) d (x i , x j ) 0 лишь для xi = xj ;

в) d (x i , x j ) d (x j , xi ) ;

г) d (x i , x j ) d(x i , x k ) d(x k , x j ) ,

где xi, xj, xk − любые три точки из En (так называемое “правило треугольника”).

Значение функции d для двух заданных точек xi , x j эквива-

лентно расстоянию между Оi и Оj.

В качестве примера функций расстояний приведем наиболее употребительные:

1) евклидово расстояние

2) сумма абсолютных отклонений, называемая иногда метрикой города, получившей такое название в силу следующей интерпретации – это длина пути между двумя перекрестками в городе с прямыми ортогональными улицами

где S X1 – матрица, обратная матрице рассеяния (см. (9.3)) .

Расстояние Махаланобиса часто называют обобщенным евклидовым расстоянием; оно инвариантно относительно невырожден-

ного линейного преобразования y=Bx, т.е. dM ( y i , y j ) =

dM (x i , x j ) .

Первые две метрики представляют частный случай так называемой l p -метрики (метрики Колмогорова):

206

где wi – некоторый неотрицательный «вес», пропорциональный степени важности i-й компоненты при решении вопроса об отнесении объекта к тому или иному классу.

Расстояния между N объектами могут быть сведены в квадрат-

ную симметричную матрицу расстояний

Понятием, противоположным расстоянию, является понятие сходства. Мерой сходства называют неотрицательную вещественную функцию, удовлетворяющую следующим аксиомам:

2)s(x i , x j ) 1;

3)s(x i , x j ) s(x j , x i ) .

Значения функции сходства элементов множества О можно объединить в матрицу сходства

207

Величину sij обычно называют коэффициентом сходства. При-

ведем в качестве примера функции сходства для объектов, описываемых дихотомическими признаками, т.е. такими, которые могут принимать значения нуль или единица. Для заданных точек Xi и Xj

обозначим через ij11 ij00 число совпадающих единичных (нуле-

вых) координат, через ij10 – число координат, имеющих 1 в X i и 0

в X j , сходным образом определяется ij01 . Мерами сходства будут функции:

1)ij11 /( ij11 ij10 ij01) ;

2)( ij11 ij00 ) / n ;

3)ij11 / n .

Заметим, что подбирая подходящее преобразование, можно перейти от мер расстояния к мерам сходства.

Меры близости и расстояния могут задаваться также с помощью так называемых потенциальных функций F(u,v) = f ( d ( u , v )) , где u и v – любые две точки из Еn; d ( u , v ) – метрика. В качестве при-

мера приведем две такие функции:

F(u,v) = exp ( - a d 2 ( u , v )), a > 0; F(u,v) = (1 + a d 2 ( u , v )) - 1.

Выбор той или иной метрики (или меры близости) является ответственным этапом кластерного анализа, оказывая существенное влияние на результаты разбиения объектов на классы. В каждой конкретной задаче этот выбор должен производиться с учетом целей исследования, физической и статистической природы наблюдений, полноты априорных сведений о характере распределения

208

наблюдений. Приведем несколько рекомендаций по выбору метрики.

1.Если известно, что наблюдения извлекаются из нормальных генеральных совокупностей с одной и той же матрицей ковариаций, то целесообразно использовать расстояние Махаланобиса.

2.Использование обычного евклидова расстояния можно признать оправданным, если:

а) компоненты вектора наблюдений взаимно независимы и имеют одну и ту же дисперсию;

б) отдельные признаки x1,...,xn однородны по физическому

смыслу и одинаково важны с точки зрения задачи классификации;

в) пространство признаков совпадает с геометрическим пространством (n= 1, 2, 3).

В некоторых задачах связи между объектами вытекают из сущности самой задачи, требуется лишь «подкорректировать» их с тем, чтобы они удовлетворяли аксиомам мер расстояния или сходства. Примером может служить задача классификации с целью агрегирования отраслей народного хозяйства, решаемая на основе матрицы межотраслевого баланса.

Рассмотрим теперь меры близости между кластерами. Введе-

ние понятия расстояния между группами объектов оказывается целесообразным при конструировании многих процедур кластериза-

ции. Пусть Кi – i-й кластер, содержащий Ni объектов; x(Ki ) –

Рассмотрим наиболее употребительные расстояния между кластерами:

1) расстояние, измеряемое по принципу ближайшего соседа

(nearest neighbour)

209

2) расстояние, измеряемое по принципу дальнего соседа (furthest neighbour)

3) расстояние, измеряемое по принципу средней связи между кластерами

4) расстояние, измеряемое по центрам тяжести кластеров

Dcp Kl , Km d x(K l ), x(Km ) .

5) мера близости, основанная на потенциальной функции

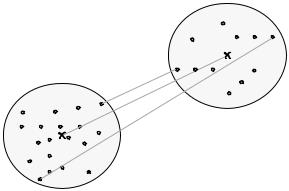
Иллюстрация трех из приведенных мер представлена на рис. 9.1.

Km

Dmin

Рис.9.1. Примеры расстояний между кластерами

210