Назаметдинов Анализ данных 2012

10.1. Вычисление главных компонент

Вычисление весовых коэффициентов будем проводить последовательно, начиная с первой главной компоненты. Значение первой главной компоненты z1 для i-го объекта (i=1,2,…,N) составит

Оценка дисперсии D(z1) центрированной переменной z1 есть по определению среднее квадрата ее значений. Таким образом,

ходных признаков 1 2 n . Эту оценку обозначим ˆ . Выраже- x , x ,..., x C

ние (10.5) примет вид:

(10.5а)

Вектор параметров a1 необходимо подобрать так, чтобы дис-

персия D(z1) была максимальной. Если на параметры не накладывать никаких ограничений, то, очевидно, такая задача не имеет ко-

нечного решения. Потребуем, чтобы норма (длина) вектора a1 , равнялась единице:

Для максимизации (10.5а) при ограничении (10.6) воспользуемся методом неопределенных множителей Лагранжа. Определим функцию

ˆ ,

(a1, ) a1Ca1 λ1(a1a1 1)

где λ1 – множитель Лагранжа.

Дифференцирование (a1, ) по отдельным элементам вектора a1 компактно может быть записано так:

231

ˆ .

наибольшее собственное значение матрицы С

При поиске значений элементов вектора a2 , кроме ограничения

на норму вектора, аналогичного (10.6), требуется обеспечить ортогональность векторов значений первой и второй главных компо-

нент Z1 и Z2 . Так как скалярное произведение ортогональных век-

Умножая последнее равенство слева на a1 и принимая во внимание условие нормировки (10.6), получаем:

232

где в качестве 2 выбирается второе по величине собственное зна-

лученные в результате n собственных векторов матрицы составят ортогональную матрицу:

An n [a1 a2 ...a j ...an ] .

В итоге, значения главных компонент задаются матрицей:

поскольку A′A = I в силу ортогональности собственных векторов. Следовательно, главные компоненты попарно некоррелированы,

а их дисперсии совпадают с собственными значениями ковариационной матрицы исходных переменных.

233

вых собственных значений, и изменения в переменных x1, x2 ,..., xn

могут быть полностью выражены с помощью n-k независимых переменных. При отсутствии нулевых собственных значений некоторые λi могут оказаться весьма близкими к нулю, так что суще-

ственный вклад в суммарную дисперсию будут вносить первые несколько главных компонент.

Суммарная дисперсия исходных переменных, равная следу мат-

Здесь мы воспользовались свойством неизменности следа произведения матриц при перестановке сомножителей, т.е. tr(AB)=tr(BA) (предполагается, что произведение ВА существует). Тогда отношения

характеризуют пропорциональный вклад каждого вектора, представляющего главные компоненты, в суммарную дисперсию исходных переменных.

Накопленные отношения

показывают относительную долю в суммарной дисперсии исходных переменных, которая приходится на первые k главных компонент. Задавшись некоторым порогом , для дальнейшего анализа оставляют те первые k΄ главных компонент, для которых

Qk 1 , а Qk .

В заключение сделаем два замечания.

1. Переход к главным компонентам наиболее естественен и эффективен, когда исходные признаки имеют общую физическую природу и измерены в одних и тех же единицах. Если это условие

234

не имеет место, то результаты иcследования с помощью главных компонент будут существенно завиcеть от выбора масштаба и природы единиц измерения. В качестве практического средства в таких ситуациях можно рекомендовать переход к вспомогательным

безразмерным признакам xi*, i 1,2,...,n нормированием исходных

знака.

2. Аналитически доказано, что переход от исходного n-мерного пространства к m-мерному пространству главных компонент сопровождается наименьшими искажениями суммы квадратов расстояний между всевозможными парами точек наблюдений, расстояний от точек наблюдений до их общего центра тяжести, а также углов между прямыми, соединяющими всевозможные пары точек наблюдений с их общим центром тяжести

Геометрическая интерпретация главных компонент. Для n-

мерного вектора a с ковариационной матрицей С можно постро-

ить так называемый эллипсоид рассеяния:

a a C 1 a a n 2 ,

где a – вектор средних значений элементов a .

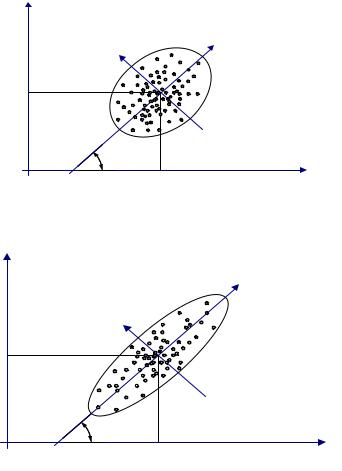
Точки, соответствующие наблюдениям вектора а, будут располагаться примерно в очертаниях этого эллипсоида. На рис. 10.1 приведена двумерная иллюстрация эллипсоида рассеяния.

В методе главных компонент исходные наблюдения предполагаются центрированными. Переход к центрированным наблюдениям означает перенос начала координат в точку (x1, x2 ) . Затем оси

координат поворачивают на угол α так, чтобы ось z1 шла вдоль главной оси эллипсоида рассеяния. Наблюдения в новых координатах z1 и z2 станут независимыми.

Чем теснее наблюдения группируются около главной оси эллипсоида рассеяния, являющейся теперь новой координатой z1, тем менее значащим является для исследователя разброс точек в направлении оси z2, а следовательно, и сама эта координата (рис.10.2).

235

10.2. Статистические свойства главных компонент

При вычислении матрицы весовых коэффициентов использова-

ˆ

лась выборочная ковариационная матрица C , полученная по результатам наблюдений конечного числа N объектов. Если объем выборки увеличить за счет привлечения дополнительных объектов,

236

то естественно ожидать, что пересчет главных компонент изменит оценки собственных значений и элементов собственных векторов. Степень изменения оценок зависит от N. Чем больше N, тем меньше эти изменения. Иными словами, можно ожидать, что для больших выборок главные компоненты совпадают с главными компонентами всей генеральной совокупности.

Здесь рассматриваются некоторые оценки близости выборочных и теоретических характеристик главных компонент. Как принято в статистике, выборочные значения в отличие от теоретических будем помечать знаком ^ над буквами.

Прежде всего следует заметить, что проведение подобных оценок возможно, если принять некоторые допущения, а именно: исследуемая генеральная совокупность подчиняется многомерному нормальному закону, а извлеченные из нее выборки взаимно независимы. Приведем без доказательства ряд утверждений.

1. Собственные значения и собственные векторы, найденные по выборочной ковариационной матрице, являются оценками максимального правдоподобия и обладают всеми хорошими свойствами этих оценок (состоятельность, асимптотическая эффективность).

ны со средним значением, равным нулю, и дисперсией, равной 2λi2 , и независимы от других выборочных собственных значений.

Последнее утверждение дает основу для нахождения доверительного интервала для i-го собственного значения λi . А именно:

стандартного нормального распределения, которое находится из таблиц из условия

P U u 2 1 2α .

Проиллюстрируем определение главных компонент на примере. Пример. Выборочная ковариационная матрица имеет вид:

237

Решая получающееся уравнение относительно , находят: λ1 28,33; λ2 16, λ3 0,67 .

Заметим, что программы вычисления собственных значений и собственных векторов входят практически во все пакеты прикладных программ по статистике.

Для рассматриваемого примера найдем первый собственный вектор а1. Как следует из (10.7) и (10.6)

Накопленные отношения, показывающие долю суммарной дисперсии, обусловленной первой и второй и всеми тремя главными компонентами, составляют:

Полученные значения позволяют сделать вывод, что 63% изменчивости исходных переменных приходится на долю первой главной компоненты:

238

z1 0,94x1 0,35x3 .

Первые две главные компоненты практически полностью «выбирают» разброс исходных переменных.

10.3. Приложения главных компонент

10.3.1. Регрессия на главные компоненты

Возможность сокращения числа предикторов за счет выделения главных компонент используется в регрессионном анализе в случае нехватки числа степеней свободы либо как способ борьбы с мультиколлинеарностью. Процедура применения достаточно очевидна:

1)по матрице F значений базисных функций находят главные компоненты;

2)отбрасывают те из них, которые соответствуют малым значениям собственных чисел;

3)ищется регрессия на оставшиеся главные компоненты;

4)от оценок коэффициентов регрессии на главные компоненты

переходят к оценкам на исходные базисные функции.

Пусть ищется линейная регрессия у=b1x1+b2x2+b3x3+-b4x4+u на четыре центрированные переменные х1,х2,х3,х4.

Из четырех главных компонент ограничимся двумя первыми:

z1 a11x1 a21x2 a31x3 a41x4 ; z2 a12x1 a22x2 a32x3 a42x4.

Регрессия у на z1 и z2 имеет вид:

y c1z1 c2 z2 e c1(a11x1 ... a41x4 ) c2 (a12x1 ... a42x4 ) e(c1a11 c2a12)x1 ... (c1a41 c2a42)x4 e .

Если бы использовались все четыре главные компоненты, то оценки последнего уравнения совпали бы с оценками прямой ре-

грессии у на х1,х2,х3,х4: bi c1ai1 c2ai2 c3ai3 c4ai4 , i=1,2,3,4.

Сравнивая коэффициенты при xi, видим, что отбрасывая часть главных компонент (при условии, что соответствующие λ≠0), мы привносим смещение в оценки коэффициентов регрессии.

239

Последнее выражение показывает, что при отбрасывании компонент с малыми значениями λ, исключаются большие по модулю сˆ , т.е. мы приходим к редуцированным оценкам.

10.3.1.Сингулярный спектральный анализ

Вглаве, посвященной временным рядам, мы ограничились рядами сравнительно простой структуры с единственной периодической составляющей – сезонной компонентой. В реальных рядах периодическая составляющая часто имеет более сложную структуру

ихарактеризуется переменными периодом и амплитудой. Выделение и представление структурных компонент ряда,

включая все возможные периодики, имеет большое прикладное значение. Оказалось, что главные компоненты могут помочь в выявлении структуры ряда и его прогнозировании. В зарубежной

литературе метод получил название сингулярный спектральный анализ (Singular Spectrum Analysis – SSA), в отечественной испо-

льзуется также название «метод гусеница». Идея метода состоит в представлении одномерного ряда в виде совокупности его представительных фрагментов (траекторной матрицы) с последующим разложением исходного временного ряда (точнее, его траекторной матрицы) по базису, порождаемому им самим. Метод не требует изначальной спецификации модели исследуемого временного ряда. Тем не менее он позволяет разложить ряд на элементарные составляющие, что по ним оказывается возможным выявить тренд или найти периодические составляющие.

Метод "гусеница" содержит четыре этапа:

1.Развёртка одномерного ряда в многомерный.

2.Выделение главных компонент – сингулярное разложение выборочной ковариационной матрицы.

3.Отбор главных компонент.

4.Восстановление одномерного ряда.

Перейдём к более подробному описанию каждого этапа.

240