
Назаметдинов Анализ данных 2012
.pdf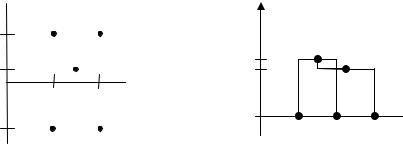
ный индекс, равный расстоянию (1– ε )2, оказывается меньше по сравнению с индексом К1, равным 1. Налицо инверсия, поскольку нарушено требование 2, предъявляемое к индексам: К1 К3
ν(К1) < ν(К3) (см. рис.9.4,б).
o1 |
o2 |
|
|
1 |
|
|
|
ε |
1 |
|
|
(1-ε)2 |
|
|
|
1 |
2 |
|
|
-1 |
v1 |
v2 |
v3 |
o4 |
o5 |
|
|
|
а) |
б) |
|
Рис.9.4. Пример инверсии для евклидовой метрики: а) − исходная конфигурация; б) − инверсия
Достаточные условия, когда оцифрование является и индексацией, содержатся в теореме Миллигана. Эта теорема опирается на рекуррентную формулу Жамбю, которая позволяет пересчитывать расстояния между имеющимся кластером К и вновь образованным K =Ki Kj (K Ki, K Kj), используя расстояния и индексы, полученные на предыдущих шагах:
d ( K , K ) = a 1 d ( K , K i )+ a 2 d ( K , K j ) + a 3 d (K i , K j )+ a 4 ν (K )+ + a 5 ν ( K i ) + a 6 ν ( K j )+ a 7 d ( K , K i ) – d ( K , K j ) ,
где ai – числовые коэффициенты, зависящие от метода определения
расстояния между кластерами. Так, при
а1=а2= –а7=1/2 и а3=а4=а5=а6=0
приходим к расстоянию, измеренному по принципу «ближайшего
соседа», а при
а1=а2=а7=1/2 и а3=а4=а5=а6=0 –
«дальнего соседа».
221
Теорема Миллигана. Пусть h – иерархия на О, полученная с использованием метрики d(К1,К2), для которой справедлива формула Жамбю. Тогда, если
а1+а2+а3 1, аj 0 для j=1,2,4,5,6 и а 7 – min ( а 1 , а 2 ),
то отображение , задаваемое формулой (К1 К2)=d(К1,К2) и условием ν({Оi})=0, i=1,2, …,N, является индексацией.
В заключение отметим, что если рассечь дендрограмму горизонтальной линией на некотором уровне *, получаем ряд непересекающихся кластеров, число которых равно количеству «перерезанных» линий (ребер) дендрограммы; состав кластера определяется терминальными вершинами, связанными с данным «перерезанным» ребром.
9.6. Анализ и интерпретация результатов кластерного анализа
В ходе исследования получающихся в процессе кластеризации подмножеств естественен вопрос: не является ли та или иная пара подмножеств однородными, что позволило бы объединить их в один кластер. Решение подобной задачи возможно в рамках вероятностной модели.
Пусть D(K1) = {d(xi,xj), xi,xj K1} – множество расстояний меж-
ду различными M элементами кластера K1; D(K2) = {d(xi,xj), xi,xj K2} – между N элементами кластера K2; D(K1,K2) = {d(xi,xj), xi K1, xj K2} – множество расстояний между элементами из разных кла-
стеров. Образуем две выборки А и В: А = D(K1) D(K2), содержащая внутрикластерные расстояния, и В = D(K1,K2), составленную из межкластерных расстояний. Если число элементов в каждой ыборке достаточно велико, то для проверки гипотезы об однородности можно воспользоваться критерием Уилкоксона.
В общем случае, разбиение, полученное с помощью тех или иных процедур кластерного анализа, следует признать удачным, если оно допускает содержательную интерпретацию. Тем самым определяются уровни качественной переменной, отвечающие кластерам. Интерпретация предполагает осмысление возможных причинных механизмов обособления полученных групп объектов.
222
Определенную помощь в этом процессе могут оказать количественные оценки. Известны десятки критериальных величин, используемых в кластерном анализе. Статистические эксперименты с массивами данных, кластерная структура которых была известна заранее, позволили выявить наиболее информативные критерии. Это – величина объясненной доли общего разброса Т и точечнобисериальный коэффициент корреляции Rb. Отметим, правда, что эксперименты проводились с евклидовой метрикой, существенной при обосновании данных критериев.
Пусть исходное множество О объектов разбито на m кластеров. Воспользуемся следующими тремя характеристиками степени рассеяния объектов из О:
|
|
|
|
N |
|
|
|
|
||
общее рассеяние S0 d 2 (x i |
, x) ; |
|||||||||
|
|
|
|
i 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
m |
|
|
межгрупповой разброс S1 N j d 2 (x(K j ), x) ; |
||||||||||
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
m |
|
внутригрупповой разброс S2 d 2 (x i , x(K j )) , |
||||||||||
|
|
|
|
|
|
|
|
|
j 1 x i K j |
|
|
1 |
N |
|
|
|
|
|
|
|
|
где x |
X i |
– среднее всего множества объектов, иначе общий |
||||||||
|
||||||||||
|
N |
|
|
|
|
|
|
|
||
|
|
i 1 |
|
|
|
|
|
|
|
|
центр тяжести, |
x(K j ) |
1 |
|
|
x i |
– центр тяжести j-го кластера, Nj |
||||
N |
j |
|
||||||||
|
|
|
|
|
i |
K j |
|
|||
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|||
– число объектов в кластере Кj.
Можно показать (см. контрольные вопросы и упражнения к главе), что для евклидова расстояния общий разброс распадается на
межгрупповое и внутригрупповое рассеяния, т.е.
S0 = S1 + S2. (9.7)
Доля межгруппового разброса в общем рассеянии T = S1/S0 показывает долю общего разброса, объясненного классификацией. Легко видеть, что T = 1 – S2/S0. Из последней формулы следует, что
223

чем компактнее группы, тем ближе Т к единице, и, соответственно, лучше качество разбиения. Очевидно, 0 Т 1.
Точечно-бисериальный коэффициент корреляции Rb вводится следующим образом. Каждой паре объектов Оi и Оj кроме расстояния dij ставится в соответствие еще индекс эквивалентности δij, равный 1, если оба объекта принадлежат одному и тому же кластеру, и 0 – в противном случае:
1, |
Oi ,O j Km ; |
|
|
|
|
δij (Oi ,O j ) |
0, |
Oi Km , O j Kn , Km Kn . |
|
||
|
|
|
Коэффициент Rb подсчитывается как обычный коэффициент корреляции между dij и бинарной величиной δij по всем парам объектов.
Кроме Т и Rb упомянем еще две характеристики, носящие качественный характер. Группу объектов Кj, для которой средний квадрат внутригруппового расстояния меньше среднего квадрата расстояния до общего центра в исходной совокупности, т.е.
|
N j |
S0 |
|
1 |
d 2 (x i , x(K j )) |
, |
|
|
|
||
N j i 1 |
N |
|
|
называют собственно кластером.
Если для группы Кj максимум квадрата расстояния до центра группы X j не превосходит среднего до общего центра, т.е.
maxi d 2 (xi, x(K j )) ) < S0 /N,
x K j
то такую группу называют сгущением. Из двух разбиений одного и того же множества объектов предпочтительным признается то, у которого больше собственно кластеров и/или сгущений.
Интерпретация полученных групп базируется обычно на тщательном анализе состава объектов, попавших в одну группу. Определенную помощь здесь может оказать анализ статистических характеристик переменных, описывающих объекты. В частности, переменные, имеющие наименьший разброс, т.е. наименее изменчивые в пределах группы, могут выступать в качестве индикатора, полезного при интерпретации группы.
224
9.7. Кластерный анализ номинальных данных
Рассмотрим случай, когда характеристики объектов описываются номинальными переменными, либо кластеризации подлежат объекты, представляющие собой так называемые транзакционные данные: наименования товаров в отдельной покупке (заказе), список ключевых слов статьи; множество симптомов пациента; характерные фрагменты изображения. Применять для кластеризации объектов с номинальными признаками рассмотренные выше алгоритмы неэффективно, а часто – невозможно. Сдерживающими факторами выступают сложность задания метрики для вычисления расстояния между качественными атрибутами, а также необходимость попарного сравнения объектов между собой на каждой итерации. Для таблиц с миллионами записей и тысячами полей это проблематично.
Поэтому в последнее десятилетие ведутся активные исследования в области разработки масштабируемых алгоритмов кластеризации качественных данных.
Алгоритм CLOPE, который рассматривается в данном параграфе, предложен группой китайских ученых [29]. Он обеспечивает более высокую производительность и лучшее качество кластеризации в сравнении с другими алгоритмами.
В основе алгоритма кластеризации CLOPE лежит идея максимизации глобального функционала качества, который повышает близость объектов в кластерах при помощи увеличения параметра кластерной гистограммы.
Чтобы получить некоторое общее представление об алгоритме, рассмотрим набор данных о пяти покупках (транзакциях) {(apple, banana), (apple, banana, cake), (apple, cake, dish), (dish, egg), (dish,
egg, fish)}. Для компактности описания будем обозначать транзакции первыми буквами составляющих ее элементов: транзакция (apple, banana) сокращается до ab и т.д. Проведем сравнение двух
возможных разбиений исходного множества транзакций на два кластера: (1) {{ab, abc, acd}, {de, def}} и (2) {{ab, abc},{acd, de,
def}}. Для каждого кластера рассчитывается количество вхождений в него каждого отдельного элемента транзакции, а затем вычисля-
225
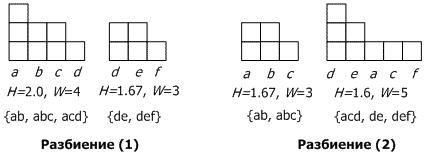
ется высота (H) и ширина (W) кластера. Например, кластер {ab, abc,
acd} имеет восемь вхождений четырех элементов: a:3, b:2, c:2, и d:1, что дает H=2,0 и W=4. На рис.9.5 показаны эти результаты гео-
метрически в виде гистограммы, с элементами, отсортированными для наглядности в порядке, обратном количеству их вхождения в кластер.
Рис. 9.5. Гистограммы двух разбиений
Из двух разбиений предпочтительным оказывается первое. Действительно, оcтавляя в стороне две идентичных гистограммы для кластера {de, def} и кластера {ab, abc}, другие две гистограммы разного качества. Гистограмма для кластера {ab, abc, acd} содер-
жит четыре различных элемента и имеет площадь S в 8 блоков (H=2,0, H/W=0,5), а кластер {acd, de, def} имеет пять различных
элементов с такой же площадью S=8 (H=1,6, H/W=0,32). Очевидно, что разбиение (1), лучше, поскольку предпочтительней больше наложений транзакций друг на друга в одном кластере.
Из приведенного выше примера, видно, что большее отношение высоты к ширине гистограммы означает лучшее внутрикластерное сходство. Китайские ученые использовали эту простую и очевидную идею как основу своего алгоритма кластеризации.
Однако чтобы определить целевую функцию, учитывать одно только значение высоты H недостаточно. Пусть, например, исходный набор состоит из двух транзакций {abc, def}. Они не содержат
226

общих объектов, так что разбиение {{abc, def}} и разбиение {{abc}, {def}} характеризуются одной высотой H=1.
В [29] предлагается использовать функцию G(K)=H(K)/W(K)=
=S(K)/W(K)^2 вместо H(К) как меру качества для кластера К. Теперь, разбиение {{abc}, {def}} лучше, так как G(K) каждого кластера в нем равен 1/3, что больше, чем 1/6, для кластера {abc, def}.
В общем случае показатель степени может быть и другим. Чтобы определить целевую функцию кластеризации, нужно принимать во внимание как форму каждого кластера, так и количество транзакций в нем. Для множества кластеров К={К1,...,Кk}, используется следующее определение целевой функции:
|
k |
|
|
|
|
|
|
|||
|
|
S (Ki ) |
|
|
Ki |
|
|
|
||
|
|
|
||||||||
|
|
|
r |
|||||||
G (K ) |
i 1` W (Ki ) |
|
, |
|||||||
|
|
|||||||||
r |
|
k |
|
|
|
|
|
|
||
|
|
|
|
Ki |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i 1
где Ki – число объектов в кластере Ki; r – положительное веще-
ственное число, называемое коэффициентом отталкивания.
Коэффициент отталкивания используется для регулирования уровня сходства транзакций внутри кластера. При больших значениях r транзакции из одного кластера должны разделиться по новым кластерам. Напротив, небольшое значение коэффициента отталкивания может использоваться для группирования разреженных баз данных. Транзакции, имеющие небольшое количество общих элементов, могут быть помещены в один кластер.
Алгоритм CLOPE относится к классу последовательных. При первом проходе по таблице транзакций строится начальное разбиение. Очередная транзакция помещается либо в существующий кластер, либо в новый в зависимости от того какая альтернатива обеспечит большее значение Gr(K). Последующие проходы осуществляются для повышения качества кластеризации и оптимизации целевой функции. Если никаких изменений в кластеризации не было сделано в результате предыдущего прохода, то алгоритм остановится.
227
9.8. Нечеткая кластеризация
В п.9.5 уже отмечалась размытость структуры данных, более тонко отражаемая иерархическим кластерным анализом в сравнении с раздельным. При анализе социально-экономических, медикобиологических данных встречаются ситуации, когда вопрос о принадлежности некоторого объекта к тому или иному классу не может быть решен однозначно (принадлежит – не принадлежит), решается вопрос о степени принадлежности. Решению подобного рода задач посвящены методы нечеткой классификации.
Пусть, как и прежде, О = {О1,О2, …,ОN} – множество исследуемых объектов. Нечеткое (размытое) подмножество объектов задается с помощью функции μ, сопоставляющей объекту Оi число μi=μ(Oi) (0 μ(Oi) 1), называемое степенью принадлежности объекта Оi этому подмножеству. Ясно, что для обычного подмножества μ=1 на элементах этого подмножества и μ=0 – на остальных элементах.
Размытые подмножества К1,К2, …,Кm множества О образуют разбиение на нечеткие классы, если для каждого объекта Оj О
определен m-мерный вектор μ j (μ1j ,μ2j ,...,μmj ) значений функции принадлежности, таких что
m |
|
μi |
j 1, j 1,2,...,N . |
i 1 |
|
Иными словами, разбиение задается матрицей
Μ= 
 μij
μij 
 , i=1,2,…,m; j=1,2,…,N
, i=1,2,…,m; j=1,2,…,N
c единичной суммой элементов в каждой строке; каждый столбец Mi матрицы M представляет соответствующее подмножество Кi.
Построим критерий качества разбиения на базе типичного для обычного кластерного анализа внутригруппового рассеяния. Пусть на множества объектов О, описываемых матрицей значений признаков Х, задана евклидова метрика d2. Для размытого подмножества К, задаваемого N-мерным вектором-столбцом Mi, и точки е Еn с координатами (е1,е2,…,еn) определяется так называемый
взвешенный разброс размытого множества относительно е:
228
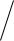
N |
n |
|
S(M , e,θ) θ(μ j ) ( Xij ei )2 , |
(9.8) |
|
j 1 |
i 1 |
|
где θ(.) – некоторая монотонная функция на отрезке [0,1], при этом
θ(0)=0, θ(1)=1.
Центром размытого множества естественно назвать точку,
доставляющую минимум выражению (9.8). Координаты ее ei*
(i=1,2,…,n) можно найти, приравняв нулю первую производную от
S(M,e,φ) по е:
N |
N |
ei* θ(μ j )Xij |
θ(μ j ) . |
j 1 |
j 1 |
За внутригрупповой разброс размытого множества К принимают взвешенный разброс относительно его центра е*, т.е. S(M,e*,φ). Если имеется некоторое разбиение на нечеткие классы, то в качестве критерия разбиения естественно взять сумму внутригрупповых разбросов по всем классам.
Алгоритмы нечеткой классификации строятся как обобщение обычных алгоритмов.
Вопросы и упражнения
1.Какой аксиоме меры сходства не удовлетворяет коэффициент корреляции?
2.Каким линейным преобразованием можно получить функцию сходства из коэффициента корреляции?
3.Изменится ли значение функции расстояния по Махаланобису, если масштаб единицы измерения уменьшить в 10 раз?
4.lp-метрика на плоскости соответствует сумме катетов прямоугольного треугольника при р=1 и длине гипотенузы при р=2. Предложите интерпретацию lp-метрики при 1<p<2.
5.В чем различие между индексацией и оцифрованием?
6.В какой шкале измеряются транзакционные данные?
7.Докажите равенство (9.7). Указание: воспользуйтесь тожде-
ством x i x (x i x j ) (x j x) .
229
10. АНАЛИЗ ГЛАВНЫХ КОМПОНЕНТ
Пусть имеется множество, состоящее из N объектов. Каждый объект описывается с помощью n переменных (признаков, факторов). Совокупность значений переменных сведена в матрицу:
x1 |
|
x1 |
|
|
1 |
|
n |
, |
(10.1) |
X |
|
|
||
xN |
xN |
|
|
|
1 |
|
n |
|
|
в которой наблюдения представлены в виде отклонений от выборочных средних, иначе говоря, центрированы, т.е.
|
|
|
|
|
i ~i |
|
|
i |
, j 1,2,...,n; i 1,2,...,N , |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x j x j |
x j |
|
||||
|
|
1 |
N |
~i |
|
|
|
|
~i |
|
|
где |
x j |
|
x j |
– среднее значение j-й переменной, x j |
– резуль- |
||||||
N |
|||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
||
тат измерения j-го признака на i-м объекте. От исходного вектора признаков
x (x1, x2 ,...,xn )
перейдем к новому множеству переменных
z (z1, z2 ,...,zn ) .
Каждую компоненту вектора z будем представлять в виде неко-
торой линейной комбинации исходных признаков, т.е. |
|
z j a1 j x1 a2 j x2 ... anj xn , j=1,2,…,n, |
(10.2) |
где a j (a1 j ,...,anj )' – вектор искомых весовых коэффициентов.
На компоненты вектора z наложим следующее требование: первая переменная z1 должна быть ориентирована по направлению максимально возможной дисперсии, вторая − по направлению максимально возможной дисперсии в подпространстве, ортогональном первому направлению, и т.д. Компоненты вектора z, удовлетворяющие этому требованию, называют главными компонентами.
230
