Назаметдинов Анализ данных 2012

предпосылки классической регрессии выполняются. В частности,

соv M[ '] M[T 1uu'(T 1)'] T 1M[uu ](T 1)T 1 (T 1)' T 1TT '(T 1) T 1T (T 1T ) I.

Воспользовавшись для преобразованных данных обычным МНК, минимизирующим остаточную сумму квадратов

получим оценку ОМНК для исходной модели:

Здесь мы воспользовались свойством произведения обратных матриц B-1A-1=(AB)-1, а также тем, что (A-1)′=(A′)-1.

Легко показать, что cov аˆОМНК =(F ′ -1F)-1.

Отметим, что использование коэффициента детерминации R2 в модели с негомоскедастичными возмущениями не вполне корректно, поскольку в преобразованной модели (4.14) уже нельзя гарантировать наличие свободного члена.

Частным случаем ОМНК является взвешенный МНК, который применяется в случае гетероскедастичных случайных возмущений, для которых ковариационная матрица является диагональной:

возмущения некоррелированы, но дисперсии σi2 , i 1, 2,..., N в

i 1

т.е. каждое отклонение входит в SR со своим весом1/ σi .

Коррелированность остатков может быть следствием неполноты

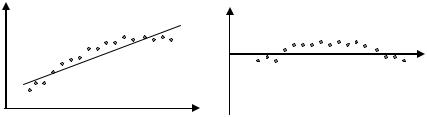
спецификации модели. Рассмотрим регрессию от одной переменной (рис. 4.1).

92

Для состоятельности оценок требуется [5], чтобы существовал plim(1/N)F′F и plim(1/N)F′u=0.

2) регрессоры коррелированы со случайным компонентом.

Коррелированность F и u приводит к смещению оценок и их несостоятельности. Проиллюстрируем это утверждение на примере парной регрессии с центрированными переменными. Как следует

ным компонентом u-a1v, приходим к случаю 2.

4) регрессия в интервальных данных. Рассмотрим вначале вопросы, касающиеся статистики интервальных данных[24].

Результат конкретного измерения можно представить как сумму

ля интересует статистика f, несмещенно оценивающая некоторый

параметр а. При подсчете статистики f в качестве аргумента вы-

~

ступает выборочные значения x , тогда как выводы должны ка-

саться f(х), поэтому интерес представляет анализ различия между

( ~ ( ). f x ) и f x

95

Одним из основных понятий в статистке интервальных данных является понятие нотны, под которой понимается максимальное по модулю расхождение между вычисленным и истинным значениями

: ~ .

статистики f N f sup f (x ) f (x) Как правило, иi есть резуль-

тат воздействия как чисто случайных факторов (статистическая ошибка с дисперсией σ2), так и метрологической ошибки Δ, привносимой измерительным прибором. Показано, если метрологическая погрешность не превышает определенного порога Δ, причем мало, а функция f(х) имеет частные производные второго порядка, то нотна аппроксимируется с точностью до малых высокого по-

Максимум среднего квадрата ошибки (на множестве возможных значений ошибок) параметра а составит

ляется состоятельной, поскольку правая его часть не стремится к нулю с ростом объема выборки. Соответственно и доверительный интервал должен быть увеличен пропорционально нотне.

Выражение (4.16) накладывает верхнюю границу на объем выборки, поскольку ошибку нельзя сделать сколь угодно малой.

где X0 и y0 - истинные значения переменных, α и γ - неизвестные малые погрешности.

Нотна оценки наименьших квадратов aˆ – это вектор, каждая координата которого – максимально возможное отклонение этой координаты изучаемого вектора aˆ , вызванное погрешностями α и γ. Таким образом, рассматриваемая нотна – это вектор Na = (N1a,

N2a, …, Nka), где

96

где sup берется по области изменения (α, γ).

В литературе приводятся оценки нотны для малых возмущений. Получение таких оценок основывается на разложении матричных выражений для оценок коэффициентов регрессии по малому параметру.

4.5.3. Нелинейная регрессия

Рассматриваемые до сих пор модели регрессии были линейными по параметрам, представляя собой взвешенную сумму базисных функций. Далеко не всегда подобная спецификация модели представляется адекватной. Если параметры входят в уравнение регрессии нелинейным образом, то говорят о нелинейной (по параметрам) регрессии. Модель специфицируется в виде

Типичный пример нелинейной регрессии – мультипликативная производственная функция с аддитивным случайным компонентом

Как и в случае линейной регрессии, для нелинейной регрессии основным методом оценивания является метод наименьших квадратов. Под оценкой МНК нелинейной регрессии (4.16) понимают то значение вектора aˆ , для которого сумма квадратов отклонений минимальна, т.е.

Нелинейность по параметрам приводит к следующим проблемам:

1)оценка МНК может вообще не существовать;

2)наличие локальных минимумов S R , что порождает проблему распознавания истинной и ложных оценок МНК;

3)вычислительные сложности при поиске точек минимума S R .

В линейной по параметрам регрессии оценка получается из системы нормальных уравнений. В предположении дифференцируе-

97

мости f можно таким же образом построить систему

нормальных уравнений, однако она уже не будет линейной относительно оцениваемых параметров. Вот почему обычно

минимизируют непосредственно S R . В основном здесь используют

метод Гаусса и его модификации, а также метод Марквардта. Практика расчетов показывает, что метод Ньютона−Гаусса хорошо работает в регрессиях, где нелинейности не слишком велики (например, регрессии, линейные в логарифмах). В регрессиях с высокой степенью нелинейности предпочтительнее метод Марквардта.

Существуют регрессии, в которых ни один из описанных методов не приводит к оценке МНК. Так, при оценивании производственных функций с постоянной эластичностью замены f a1, a2 , a3 a1(a2 K a3 1 a2 La3 ) 1a3 сходимость часто отсутствует.

Вообще-то говоря, в нелинейных регрессиях очень важно хорошее начальное приближение. В качестве такового часто используют линейное приближение. Далее, если регрессия не сводится к линейной с помощью некоторого преобразования, следует попытаться найти такую трансформацию регрессии, в которой основная часть параметров стала бы линейной. Если нелинейных параметров не больше двух-трех, то задаются сеткой для этих параметров и оценивают остальные параметры обычным МНК для каждого набора параметров сетки. В качестве начального приближения вы-

бирают то, которое доставляет минимум S R . Наличие локальных минимумов у функции S R порождает проблему идентификации

глобального минимума. Говорить, что эта проблема решена для общего случая, не приходится. Одним из практических приемов является следующий. Процесс минимизации начинают с другого начального приближения. Если процесс сойдется к старому значению aˆ , то это может служить подтверждением, что в точке aˆ достигается глобальный минимум.

98

Вопросы и упражнения

1.Что понимается под ошибками спецификации в широком и узком смыслах?

2.В каких случаях недобор базисных функций не приводит к смещенности оценок коэффициентов регрессии?

3.В чем состоит различие между строгой и нестрогой мультиколлинеарностью?

4.Чем чревата мультиколлинеарность в регрессионном анализе?

5.Какой геометрический смысл имеет мера мультиколлинеар-

ности – минимальное характеристическое число матрицы F′F?

6. Какие меры мультиколлинеарности считаются наиболее информативными?

7. В чем состоят достоинства и недостатки метода отсева базисных функций?

8. Какое количество уравнений регрессии можно построить, имея k базисных функций?

9. Как ведет себя норма вектора оценок коэффициентов регрессии при возрастании степени мультиколлинеарности?

10. От какого свойства оценок коэффициентов регрессии необходимо отказаться при использовании ридж-оценок?

11. Как следует пополнять матрицу значений базисных функций для уменьшения коллинеарности?

12.Какие преимущества дает введение фиктивных переменных?

13.В чем заключается сходство и различие logit- и probit- моделей регрессии?

14.Покажите, что ковариационная матрица преобразованных

переменных v T 1u является скалярной.

15.Какой критерий включения регрессоров используется в пошаговой процедуре отбора?

16.Докажите, что оценка обычного МНК является несмещенной

для случая cov u= .

17. Когда случайность матрицы значений базисных функций не приводит смещенности оценок коэффициентов регрессии?

18. Что показывает нотна?

99

5. ДИСПЕРСИОННЫЙ АНАЛИЗ

Вп.4.2 рассматривался вопрос включения в регрессию качественных переменных. В случае, когда регрессорами являются только качественные переменные, общепринятым методом исследования выступает дисперсионный анализ (ДА).

Взависимости от числа регрессоров, называемых в ДА факторами, говорят об одно-, двух-, многофакторном ДА. Сами факторы полагаются неслучайными (модель с постоянными эффектами) либо случайными (модель со случайными эффектами). В модели с постоянными эффектами речь идет в основном о сравнении средних значений количественной переменной при различных значенииях факторов, тогда как в моделях со случайными эффектами интересует доля изменчивости, вносимая отдельными факторами. Ниже

рассматривается первая модель, для которой ДА часто называют одно-, двух-, многофакторной классификацией.

5.1. Однофакторный дисперсионный анализ

Имеется количественная переменная у, определяемая качественной переменной, иначе фактором, принимающим р дискретных значений (уровней). Так, фактором может быть «поставщик», уровнями – определенные фирмы-поставщики, переменной у– срок службы поставляемого товара. В качестве исходных данных выступает выборка, содержащая ряд наблюдений на каждом из уровней фактора (по нескольку экземпляров определенного товара от каждого поставщика). Необходимо ответить на вопрос: различаются ли по сроку службы объекты от разных поставщиков.

Модель однофакторного анализа:

уровня фактора. Параметр m обозначает некоторую точку отсчета, ai – эффект (вклад) i-го уровня фактора, uij – независимые, нормально распределенные случайные возмущения, удовлетворяющие пятой предпосылке классической регрессии (п.3.1).

100