Назаметдинов Анализ данных 2012

Для прямоугольных таблиц используются меры связи, основанные на Х 2, в частности, 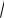X 2 / N . Известны также информаци-

онные меры связи, основанные на понятии энтропии.

Пусть случайная величина х принимает конечное множество значений х1, х2, …,хk с вероятностями р 1 , р 2 , … , р k . Величину

i 1

называют энтропией и рассматривают как меру неопределенности х. Энтропия неотрицательна, принимает минимальное значение, равное нулю, в отсутствие неопределенности, и максимальна, когда

мающей значения (х1,y1),…,(x1,yl),…, (хk,y1), …,(хk,yl) с вероятностями p11,..., p1l ,..., pk1,..., pkl , энтропия определяется аналогично:

Можно показать, что H(x,y)=H(x)+H(y) тогда и только тогда, когда х и у независимы, в противном случае H(x,y) ≤ H(x)+H(y). Основываясь на описанных свойствах энтропии, естественно ввести так

называемую информационную меру зависимости х и у:

I(x,y)= H(x) + H(y) – H(x,y).

Ясно, что I(x,y)≥ 0 и обращается в нуль, если х и у независимы.

Взаключение отметим, что для многомерных таблиц с большим числом уровней переменных применяют более сложные методы анализа, в частности, логарифмически линейные модели.

Вкачестве примера использования порядковых статистик рассмотрим задачу сопоставления наборов данных.

2.3.Сопоставление наборов данных

Результаты наблюдений одной и той же переменной могут быть получены различными способами, характеризоваться разными уровнями качественной переменной, например результаты опроса

41

объемы выборок х и у.

Если расчетное значение t-статистики tр окажется меньше табличного tТ[q,M+N-2], то гипотеза однородности принимается на уровне значимости q.

ческих ожиданий отвергается на уровне значимости q = 0,05. Строго говоря, нуждается в проверке гипотеза о равенстве дисперсий. В предположении нормальности распределений можно воспользо-

Fp 6449 1,31 , FТ[0,95;70;59]=1,53. Поскольку Fp<FT гипотеза равенства

дисперсий принимается на уровне надежности 0,95.

Если нет оснований считать дисперсии равными, следует воспользоваться критерием Крамера–Уэлча, который основан на статистике

M N (x y) .

T

Nsx2 Ms2y

Распределение Т Крамера-Уэлча с ростом объема выборки довольно быстро сходится к нормальному N(0;1), так что даже при сравнительно небольших объемах выборок аппроксимация вполне

43

H1: G(x)=F(x-d), d≠0,

хорошо зарекомендовали себя удобные в применении критерии Манна–Уитни, Уилкоксона. Гипотеза сдвига является естественной при проверке эффекта обработки в предположении, что функция распределения погрешностей измерения произвольна, но не меняется при переходе от объекта к объекту.

Рассматриваются две выборки х1,х2, … ,хM с законом распределения F(x) и y1,y2, … ,yN с законом распределения G(x). Без ограничения общности можно считать, что M≤N. Полагается, что F(x) и G(x) непрерывны, а потому достоверно утверждение, что в выборках нет совпадающих чисел. Проверяется гипотеза H0 об однородности выборок, т.е. H0: F(x) = G(x). В качестве альтернативы рассматривается гипотеза H<: F(x) ≤ G(x) (левосторонняя альтернатива

P(xi<yj)<0,5) либо H>: F(x) ≥ G(y) (правосторонняя альтернатива

P(xi<yj)>0,5).

Критерий Манна–Уитни основан на подсчете числа случаев U, когда xi<yj (i=1,2,…,M; j=1,2,…,N) для всех MN пар; критерий Уилкоксона – на подсчете суммы рангов W, присвоенных элементам одной из выборок, в вариационном ряду, составленном из элементов обеих выборок.

Пусть, например, первую выборку составляют числа 17 и 14, вторую – числа 13, 18, 15. Поскольку 17 меньше 18, 14 меньше 18 и 15, то U=1+2=3. Для подсчета W образуем вариационный ряд для объединенной выборки – 13, 14, 15,17,18. Тогда ранги элементов первой выборки суть 4, 2, а второй – 1, 5, 3.

В общем случае ранги составляют числа от 1 до M+N. Обозначим ранги наблюдений выборки x r1, r2, …, rM. Сумму рангов W =

r1+ r2+ …+ rM называют статистикой Уилкоксона. W может при-

нимать значения от M(M+1)/2 (cумма рангов от 1 до M), если все

элементы выборки x оказались меньше любого из элементов выборки y, до MN + N(N+1)/2 (сумма рангов М+1, М+2, …, М+N),

если все элементы выборки y оказались больше любого из элементов выборки х.

Можно показать, что статистики U и W линейно связаны: U=MN+M(M+1)/2-W, так что обычно работают с одной из них. Мы

45

ограничимся критерием Уилкоксона как одним из самых известных инструментов непараметрической статистики.

При справедливости гипотезы однородности H0 любая из (M+N)! перестановок равновероятна и не зависит от вида распределений F и G. Позиции r1, r2, …, rM в объединенной выборке элементы первой выборки могут занять M! способами, причем каждая из перестановок повторяется N! раз, так что вероятность набора r1, r2, …, rN составит M!N!/(M+N)!. Если перебрать все возможные способы получения той же самой суммы W = r1+ r2+ …+ rM, но с другими позициями выборки х в объединенном вариационном ряду, получим распределение вероятностей суммы рангов W. Если, как в вышеприведенном примере, M=2, N=3, то сумму рангов 5, образуют элементы первой выборки, занявшие в объединенной выборке места 1 и 4, 2 и 3. Распределение W симметрично относи-

тельно точки M(M+N+1)/2, так что M[W] = M(M+N+1)/2. Дисперсия W вычисляется по формуле D[W] = MN(M+N+1)/12.

Если число наблюдений в выборках невелико (менее 20), пользуются таблицами W-распределения. Таблица содержит верхние критические значения WT[q,M,N] для фиксированного уровня значи-

мости q, т.е. значения, для которых P(W ≥ WT[q,M,N]) = q. Если расчетное значение статистики Уилкоксона Wр превысит табличное,

т.е. Wр ≥ WT[q,M,N], гипотеза однородности отвергается в пользу правосторонней гипотезы. Если же в качестве альтернативной выступает левосторонняя гипотеза, то понадобится нижнее критическое значение W. В силу симметричности W-распределения нижнее кри-

тическое значение есть M(M+N+1) - WT[q,M,N]. Так что, при Wр ≤ ≤M(M+N+1) - WT[q,M,N] принимается левосторонняя альтернатива.

Если объемы выборок достаточно велики, используют нормиро-

при этом близко к нормальному с нулевым математическим ожиданием и единичной дисперсией. При уровне значимости q=0,05 гипотеза об однородности выборок принимается, если расчетное значение модуля Wp* окажется меньше 1,96.

46

Парные наблюдения

Пусть теперь для каждого объекта Оi (i=1,2,…,N) выборки фиксируются две случайные величины xi, yi, иначе, случайные пары (xi, yi). Здесь наблюдения над объектами полагаются взаимно независимыми, однако между xi и yi одного и того же объекта независимость не требуется. Вычислим zi = xi-yi , возьмем абсолютные разности |z1|,…,|zN| и присвоим полученным числам ранги от 1 до N в порядке их возрастания и затем найдем сумму рангов тех наблюдений, для которых zi>0. Найденную сумму, которую обозначим Тр,

называют статистикой критерия знаковых сумм (рангов) Уилкоксо-

на. Тр сравнивают с табличным значением соответствующей статистики TТ(q,N). Если Тр< TТ(q,N), то гипотеза однородности H0: P(zi

< 0) = P(zi > 0) принимается, в противном случае – отвергается в пользу гипотезы H>: P(zi < 0) < P(zi > 0).

Для больших выборок можно воспользоваться статистикой

которая имеет асимптотически нормальное распределение N(0,1) при выполнении гипотезы H0. Если Тр* > Ф-1(1- q), то H0 отклоняется в пользу H>.

Заметим, что сравнением нескольких выборок занимается дисперсионный анализ (см.гл. 5).

Вопросы и упражнения

1.В каком случае некоррелированность двух случайных величин означает их независимость?

2.Каков по знаку КК между ростом и весом?

3.Из одной и той же нормальной двумерной генеральной совокупности извлечены две выборки, причем в одной из них из-за ошибок регистрации оказалось резко выделяющееся наблюдение. Для какой выборки значение коэффициента корреляции окажется больше (по модулю)?

47

4.Оценка парного коэффициента корреляции по выборке из 10 наблюдений оказалась равной 0,35. Можно ли утверждать, что связь между переменными значима при уровне значимости 0,05?

5.Почему коэффициенты корреляции симметричны относительно нуля, а коэффициент конкордации нет?

6.Что такое «связанные ранги»?

7.Как проверяется значимость ранговых коэффициентов корреляции?

8.Покажите, что связанные ранги могут принимать целые либо кратные ½ значения.

9.Как проверяется значимость ранговых коэффициентов корреляции?

10.Что показывает частный коэффициент корреляции?

11.Как оценить коэффициент корреляции между переменными, оцененными в разных шкалах?

12.Какие меры связи предложены для номинальных перемен-

ных?

13.В каких случаях уместно использование t-статистики при сопоставлении двух выборок?

14.В чем состоит преимущество статистики Крамера–Уэлча перед t-статистикой при сопставлении двух выборок?

15.Какие непараметрические критерии целесообразно использовать при проверке гипотезы о совпадении законов распределения двух выборок?

16.Для проверки какой гипотезы используется критерии Уилкоксона?

17.В чем различие между критериями Манна–Уитни и Уилкок-

сона?

18.Какая шкала используется в критерии Манна–Уитни?

19.В чем состоит гипотеза сдвига?

20.Какой статистикой следует воспользоваться в случае парных наблюдений?

48

3. РЕГРЕССИОННЫЙ АНАЛИЗ

Описание исследуемого объекта предполагает выделение некоторой объясняемой (целевой, зависимой, выходной) переменной у и некоторой совокупности объясняющих (входных, предикторных) переменных х1, х2, …,хn. Переменная у является случайной величиной, на распределение которой влияют как переменные х, так и различные неучтенные факторы и помехи (в том числе ошибки измерения), проявляющиеся вкупе как случайные возмущения. Объясняющие переменные могут быть либо случайными, либо детерминированными, т.е. принимающими заранее определенные значения. Исчерпывающее описание случайной величины дает функция распределения. Однако ее нахождение часто становится практически нереальной задачей в силу недостаточного объема данных. Вот почему на практике ограничиваются лишь некоторыми характеристиками функции распределения, обычно, начальными моментами.

В рассматриваемом в этом разделе классическом регрессионном анализе ищется зависимость между математическим ожида-

нием объясняемой переменной у от объясняющих переменных x1 , x2 , , xn , которые полагаются детерминированными.

Условимся в дальнейшем обозначать, как это принято в стати-

стике, реализацию (наблюденное значение) выходной переменной

… , x1N , x2N ,...,xnN . Номер наблюдения соответствует либо опреде-

ленному объекту, на котором снимаются наблюдения, либо моменту времени, если наблюдается “история” некоторого объекта. Вво-

дя вектор x (x1, x2 ,..., xn ) , наблюденные значения входных пере-

менных можно записать как x1, x2 ,..., xN . В матричных обозначениях результаты наблюдений представляются в виде:

49

Строка матрицы наблюдений Х соответствует i-му (i=1,2,…,N) наблюдению.

3.1. Предпосылки классической регрессии

нированную составляющую yi , на которую аддитивно наложено случайное возмущение u i , т.е.

При этом детерминированная составляющая специфицируется как линейная комбинация заранее известных (базисных, опорных,

где y,u − N-мерные векторы-столбцы значений детерминированной и случайной составляющих;

a (a0 ,a1,...,ak ) – вектор-столбец коэффициентов регрессии;

функций.

50