1.8.2. Вязкость. Ламинарный и турбулентный режимы течения жидкостей
Идеальная жидкость, т.е. жидкость без внутреннего трения, является абстракцией. Всем реальным жидкостям и газам присуще внутреннее трение, называемое вязкостью.
Вязкость – это свойство реальных жидкостей обмени- ваться импульсами при перемещении одной части жидкости относительно другой. Вязкость проявляется, в частности, в том, что возникшее в жидкости или газе течение после прекращения действия причин, его вызвавших, постепенно прекращается.
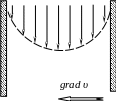Рассмотрим установившееся медленное
течение жидко- сти в круглой трубе
(рис.1.16). Ее скорость меняется от нуля в
непосредственной близости к стенкам
сосуда до максимума на оси трубы. Жидкость
оказывается как бы разделенной на слои,
которые скользят друг относительно
друга, не перемешиваясь. Такое течение
называется ламинарным (слоистым).
Рис.1.16
Между слоями жидкости действуют силы внутреннего трения, удовлетворяющие соотношению
,
(1.85) где
-
коэффициент динамической вязкости,
зависящий от природы и состояния
жидкости;
- градиент скорости, показывающий, как
быстро изменяется скорость в направле-
нии, перпендикулярном движению слоев;
- площадь слоя.
Единица вязкости
– паскаль-секунда (
).
Это вязкость такой среды, в которой при
ламинарном течении и градиенте скорости,
равном единице, возникает сила внутрен-
него трения в 1 Н на 1 м2
поверхности касания слоев.
Вязкость зависит от температуры. У жидкостей вязкость уменьшается с увеличением температуры, а у газов, наоборот, увеличивается. Это указывает на различие в них механизмов внутреннего трения.
Ламинарное течение жидкости наблюдается при неболь- ших скоростях ее движения. С увеличением скорости характер течения жидкости резко меняется. Происходит интенсивное вихревое образование и перемешивание жидкости (газа). Такое течение называется турбулентным (вихревым). Характер течения определяется значением безразмерной величины, называемой числом Рейнольдса,
,
(1.86)
где
- характерный размер сечения.
При малых
течение носит ламинарный характер.
Начиная с некоторого значения
,
называемого критическим, течение
приобретает турбулентный характер.
Один из методов определения коэффициента вязкости основан на измерении скорости падения в жидкости медленно движущихся небольших тел сферической формы.