7.11. Примеры решения задач по квантовой механике и физике атома

Пример 1. Поток моноэнергетических электронов падает нормально на диафрагму с узкой щелью шириной b= 2мкм. Найти скорость электронов, если на экране, отстоящем от щели на L= 50 см, ширина центрального дифракционного максимума  x = 0,36 мм.

Решение

Согласно гипотезе де Бройля длина волны , соответствующая частице массой m, движущейся со скоростью V, выражается формулой

= h/ mV . (1)

При дифракции на узкой щели ширина центрального дифракционного максимума равна расстоянию между дифракционными минимума- ми первого порядка. Дифракциионные минимумы при дифракции на одной щели наблюдаются при условии

b sin= k  , (2)

где k = 1,2,3… - порядковый номер минимумов.

Для минимумов первого порядка (k=1), угол заведомо мал, поэтому sin =  , и, следовательно, формула (2) примет вид

b  =  , (3)

ширина центрального максимума

x= 2L tg  = 2L  . (4)

Выражая  из (4) и подставляя его в (3), получаем

 = b x/ 2L. (5)

Искомую скорость электронов найдем из соотношения (1) с учетом формулы (5):

V= h/m = 2 h L/ m b x. (6)

После вычисления по формуле (6) получим V= 10⁶ м/с.

Пример 2. Определить длину волны де Бройля λ электрона, прошедшего ускоряющую разность потенциалов 700 кВ.

Решение

Связь длины волны де Бройля с импульсом

,

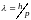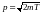где h= 6,6310^-34Джс – постоянная Планка, причём импульс вычисляется различным образом для релятивистского ( ) и нерелятивистского ( ) случаев, где m, T, E₀ – соответственно масса, кинетическая энергия, энергия покоя частицы.

Кинетическая энергия электрона, прошедшего ускоряю- щую разность потенциалов U,

Т= e U = 0,7эВ,

а энергия покоя электрона Е₀ = mc² = 0,5МэВ, т.е. в данном случае имеем дело с релятивистской частицей.

Тогда искомая длина волны де Бройля

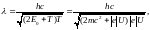
где m = 9,1110^-31кг; c =310⁸м/c; е =1,610^-19Кл.

Вичисляя, получаем λ= 1,13пм.

Пример 3. Используя соотношения неопределенностей xp_x  h/ 2 , найти выражение, позволяющее оценить минимальную энергию E электрона, находящегося в одномерном потенциальном ящике шириной l.

Решение

Из данного соотношения следует, что, чем точнее определяется положение частицы, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Неопределенность координаты электрона  x= l / 2. Тогда соотношение неопределенностей можно записать в виде

l /2  p  h/ 2,

откуда

p  h/  l.

Физически разумная неопределенность импульса p, во всяком случае, не должна превышать значения самого импульса, т.е. p  p.

Энергия E электрона, находящегося в одномерном потенциальном ящике, есть его кинетическая энергия T, величину которой можно связать с импульсом соотношением

T= p² / 2m .

Заменив p на p, получим

E_min= (h²/2 ²)/(m l²).

Пример 4. Электрон находится в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной L. Вычислить вероятность обнаружения электрона на первом энергетическом уровне в интервале L /4, равноудаленном от стенок ямы.