7.4. Движение свободной частицы

При движении свободной частицы (U = 0) ее полная энергия совпадает с кинетической. Для частицы, движущейся вдоль оси Х, стационарное уравнение Шредингера принимает вид

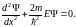(7.9)

Решением его является функция

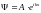, (7.10)

где k =(1/ħ)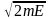 = P_x/ ħ, P_x – импульс частицы, A =const. Тогда полную волновую функцию можно записать в виде

, (7.11)

что представляет собой плоскую монохроматическую волну, распространяющуюся вдоль оси Х. Учитывая, что k =2/, для длины волны получаем  =h/P, что совпадает с формулой де Бройля. Таким образом, решение уравнения Шредингера для свободной частицы представляет собой волну де Бройля. Волны де Бройля по физическому смыслу совпадают с волновой функцией и имеют статистическую интерпретацию: их интенсивность пропорциональна плотности вероятности обнаружения частицы.

Энергия свободной частицы E = ħ²k²/(2m) может принимать любые значения, т.е. энергетический спектр её является непрерывным. Вероятность обнаружения частицы не

зависит от времени и одинакова в любой точке пространства .

7.5. Частица в потенциальной яме

Рассмотрим движение микрочастицы в одномерной прямоугольной потенциальной яме длиной l с бесконечно высокими стенками (рис.7.1). Тогда для потенциальной энергии имеем: U = 0 при 0  x  l и U = ∞ при x < 0 и x > l. Внутри ямы уравнение Шредингера имеет вид

,

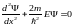или 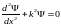, (7.12)

где k² = 2mE/ ħ².

Решение уравнения записы- вается в виде

Ψ(x)=Asin(kx)+Bcos(kx), (7.13)

где A и B – постоянные, которые определяются из граничных условий.

Вероятность нахождения частицы вне ямы равна нулю, следовательно, волновая функция вне ямы и на ее границах (в силу непрерывности) также равна 0:

Ψ(0)=Ψ(l)=0.

Из первого условия Ψ(0)= B получаем B = 0, из второго

Ψ(l)= A sin(k l)= 0

следует, что k l = n или k = n / l, где n = 1, 2, 3 … (n = 0 соответствует Ψ = 0, т.е. отсутствию частицы в яме).

Тогда для собственных значений энергии получаем выражение

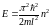, (n = 1, 2, 3 …). (7.14)

Таким образом, энергия и импульс частицы в потенциальной яме могут принимать лишь определенные, дискретные значения, т.е. квантуются (рис.7.1). Минимальное значение энергии равно E =  ²ħ²/(2ml²), т.е. частица в яме не может покоиться, что находится в соответствии с соотношениями неопределенности.

Интервал энергии между соседними уровнями составляет

.

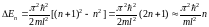Рассмотрим несколько примеров. Для молекул идеального газа (m = 10^-26кг, l = 0,1м) E_n = 10^-20n эВ, для свободных электронов в металле (m10^-30кг, l=0,1м) E_n=10 ^-16n эВ, т.е. в этих случаях можно считать, что энергия меняется непрерывно. Для электрона в атоме (m10^-30кг, l=10^-10м) E_n=10²n эВ. Следовательно, здесь квантование существенно и можно говорить лишь о дискретном спектре энергии.

Относительное расстояние между уровнями E_n/E_n  2/n уменьшается с увеличением квантового числа n, уровни располагаются ближе и спектр энергии становится квазинепрерывным.

В этом выражается принцип соответствия Бора: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.

Для определения постоянной A в волновой функции используем условие нормировки:

,

откуда .

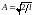Таким образом, собственные функции выражаются формулой

, n = 1, 2, 3… (7.15)

Графики собственных функций и соответствующие плотности вероятности приведены на рис.7.2.

Из рисунка видно, что в разных квантовых состояниях есть точки, в которых плотность вероятности обнаружения частицы равна нулю. Такое поведение частицы несовместимо с классическими представлениями о траектории движения и равновероятности всех положений частицы.

a) в)

Рис.7.2

Из формулы 7.15 и рис. 7.2 следует, что существуют лишь такие состояния частицы в потенциальной яме, при которых на ширине ямы укладывается целое число полуволн де Бройля. Здесь можно провести аналогию с механическими волнами. Для колеблющейся струны или закрытого акустического резонатора возникающие стоячие волны удовлетворяют такому же условию, все остальные волны существовать не могут, они затухают.