7.2. Соотношение неопределенностей

Состояние классической частицы полностью определяется ее координатами и импульсом. Зная начальное положение частицы и действующие силы, можно записать и решить уравнение движения (2-ой закон Ньютона) и тем самым определить координаты и импульс частицы для любого момента времени.

Для микрочастицы, вследствие наличия у нее волновых свойств, ситуация другая.

Пусть частица движется вдоль оси Х. Если точно определена координата частицы, то ничего нельзя сказать о ее импульсе, т.к. в соответствии с формулой де Бройля он определяет длину соответствующей волны, но понятие длины волны в данной точке не имеет смысла. Если же точно задан импульс частицы, то получаем монохроматическую волну, имеющую бесконечную протяженность, т.е. не определена координата частицы. Таким образом, координата и импульс частицы не могут быть одновременно определены точно, всегда будет погрешность. Можно показать, что это справедливо не только для координат и соответствующего импульса, но и для энергии и времени. Степень точности задается соотношениями неопределенности (соотношениями Гейзенберга):

x ^. p_x  h,

y ^. p_y  h, (7.2)

z ^. p_z  h,

t ^. E  h.

В силу малой величины h эти соотношения существенны только в микромире и не проявляются в опытах с макроскопическими телами.

Из этих соотношений следует несколько выводов:

1. микрочастица не может находиться в покое;

2. нельзя разделять полную энергию микрочастицы на кинетическую и потенциальную;

3. принципиально невозможно точно определить одновременно координату и импульс частицы.

7.3. Уравнение Шредингера

Наличие волновых свойств у микрочастиц не позволяет описывать их с помощью классического уравнения динамики, дающего возможность по заданным силам и начальным условиям найти для любого момента времени координаты частицы и её скорость (импульс). Возникла необходимость получения основного уравнения квантовой механики, которое позволило бы решить аналогичные задачи, но с учётом волновых свойств частиц. Такое уравнение было получено в 1929г. Шредингером. Оно как и уравнения Ньютона, не выводится, а постулируется как основной закон природы. Единственным доказательством его справедливости может быть лишь экспериментальная проверка выводимых из него следствий. Такую проверку уравнение Шредингера выдержало.

В нерелятивистской квантовой механике уравнение имеет вид:

, (7.3)

где 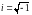, m – масса частицы, U(x,y,z,t) – потенциальная энергия частицы в силовом поле, в котором она движется, - дифференциальный оператор Лапласа, (x,y,z,t) – волновая функция частицы.

Это уравнение является волновым уравнением, решение которого позволяет найти волновую функцию (пси-функцию), однозначно описывающую состояние микро- частицы в любых условиях. Физический смысл имеет не сама волновая функция, а квадрат ее модуля, определяющий плотность вероятности пребывания частицы в данной точке пространства

(7.4)

где *- величина, комплексно сопряженная с , а dp/dV – плотность вероятности (вероятность, отнесенная к единице объема) пребывания частицы в данной точке пространства. Вероятность нахождения частицы в объеме V определяется формулой

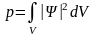. (7.5)

Связь волновой функции и вероятности приводит к следующим ограничениям на волновую функцию: она должна быть непрерывной, конечной, однозначной, иметь непрерыв- ные производные, удовлетворять условию нормировки

, (7.6)

(наличие частицы в какой либо точке бесконечного пространства - достоверное событие, его вероятность равна 1).

Если потенциальная энергия U(x,y,z) не зависит от времени, то в уравнении волны волновую функцию можно разделить на временную и пространственную части и представить его в виде

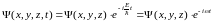, (7.7)

где E – полная энергия частицы,  = E/ ħ. Подставляя эту формулу в общее уравнение, для пространственной части волновой функции получаем:

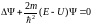. (7.8)

Это уравнение называется стационарным уравнением Шредингера или уравнением для стационарных состояний, т.к. плотность вероятности не зависит от времени. Функции , удовлетворяющие уравнению, называются собственными функциями, а значения Е, при которых существуют решения – собственными значениями энергии.

Рассмотрим несколько примеров решения этого уравнения.