4.1.4. Сложение гармонических колебаний одного направления. Биения

Результирующее движение точки, одновременно участвующей в нескольких колебаниях, во многих случаях является колебательным. Таким образом, можно говорить о сложении нескольких колебаний в одно результирующее.

Сложение гармонических колебаний одного направления с одинаковыми частотами и различными фазами осущест- вляется с помощью вектора амплитуды, позволяющего свести сложение колебаний к сложению векторов. Вектор амплитуды представляет собой вектор, величина которого равна амплитуде гармонического колебания, а угол между его направлением и осью X определяется начальной фазой (рис.4.5). Если привести вектор во вращение против часовой стрелки с угловой скоростью , то его проекция на ось X будет изменяться со временем по гармоническому закону. Следовательно, гармоническое колебание может быть задано с помощью вектора амплитуды.

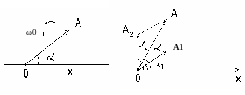
Рис.4.5 Рис.4.6

Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты, описываемых уравнениями:

, (4.20)

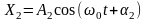. (4.21)

Представим эти колебания с помощью векторов амплитуды A₁ и A₂ и построим вектор A, представляющий результирующие колебания (рис.4.6 ).

Результирующее колебание является гармоническим с частотой ω₀

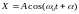, (4.22)

амплитуда которого и его начальная фаза определяются из векторной диаграммы:

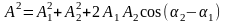, (4.23)

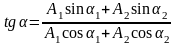. (4.24)

Рассмотрим теперь два гармонических колебания, которые происходят в одном направлении, с близкими частотами ω и ω+Δω (Δω<<ω). Пусть амплитуды складываемых колебаний одинаковы А₁=А₂= А, а начальные фазы колебаний α₁= α₂= 0.

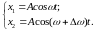(4.25)

Результирующее колебание x = x₁+ x₂, т.е.

x = А cosωt + А cos(ω+Δω)t =

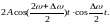= (4.26)

Учитывая что Δω<< ω, получим

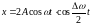. (4.27)

Так как изменяется значительно медленней, чем cosωt, результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда которого медленно

изменяется также по гармоническому закону с частотой 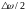. Такие колебания называются биениями (рис.4.7).

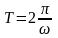
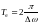
Рис.4.7

Уравнение биений имеет вид

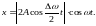(4.28)

Амплитуда колебаний равна 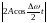, частота пульса- ций амплитуды (биений), равна разности частот складываемых колебаний (см. рис.4.7), а период биений .

4.1.5. Сложение взаимно перпендикулярных

колебаний. Фигуры Лиссажу

Пусть колебания одинаковой частоты совершаются вдоль взаимно перпендикулярных координатных осей X и Y. Выберем начало отсчёта времени так, чтобы начальная фаза первого колебания была равна нулю. Запишем уравнения колебаний таким образом

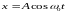, (4.29)

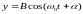, (4.30)

где - разность фаз складываемых колебаний.

Исключив из данных уравнений параметр t, получим уравнение траектории результирующего колебания.

. (4.31)

Уравнение (4.31) представляет собой уравнение эллипса, произвольно ориентированного относительно координатных осей X и Y.