4. Колебания и волны

4.1. Механические колебания и волны

4.1.1. Гармонические колебания. Дифференциальное уравнение гармонических колебаний

Колебаниями называют процессы, характеризующиеся повторяемостью во времени. Простейшими из них являются гармонические колебания, при которых колеблющиеся величины изменяются со временем по закону синуса или косинуса.

Кинематическое уравнение гармонических колебаний имеет вид

, (4.1) где х - смещение системы от своего положения равновесия; A - амплитуда колебаний; 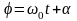- фаза колебаний; -начальная фаза ; -собственная циклическая частота.

График гармонических колебаний представлен на рис. 4.1.

Продифференцировав дважды уравнение (4.1) по времени найдём скорость и ускорение колеблющейся точки

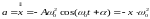, (4.2) . (4.3)

Рис. 4.1

Из (4.3), следует дифференциальное уравнение гармони- ческих колебаний

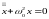. (4.4)

Решением этого уравнения является выражение (4.1).

4.1.2. Энергия гармонического колебания

С учётом уравнения (4.3), сила действующая на материальную массой m, равна

, (4.5)

где 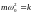- коэффициент упругости.

Упругая сила является консервативной, поэтому полная энергия механических колебаний остаётся постоянной:

Е = T+П = const.

Кинетическая энергия материальной точки, соверша- ющей прямолинейные гармонические колебания, с учётом уравнения 4.2, равна

(4.6)

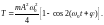или (4.7)

Потенциальная энергия материальной точки, соверша- ющей гармонические колеба- ния под действием упругой силы F, с учётом уравнения 4.5, равна

(4.8)

или

(4.9)

Частота изменения кинети- ческой и потенциальной энергий в два раза превышает частоту гармонических колеба- ний (см. рис.4.2).

Полная механическая энергия колеблющейся системы с учетом уравнений (4.7) и (4.9) равна

.

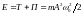4.1.3. Математический и физический маятники

Идеализированные системы, в которых колебания возникают за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий и описыва- ются уравнением (4.4), называются гармоническими осцил- ляторами. Примерами гармонических осцилляторов являются пружинный, физический и математический маятники. Колеба- ния, возникающие в таких системах при отсутствии сил трения, называются собственными гармоническими колеба- ниями.

Математическим маятником называют идеализи- рованную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке (рис.4.3).

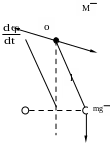
Рис.4.3 Рис.4.4

При отклонении от положения равновесия на некоторый угол математический маятник начинает совершать свобод- ные колебания. В случае малых колебаний , диф- ференциальное уравнение колебаний математического маятника имеет вид

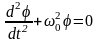, (4.10)

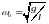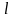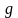где ; – длина математического маятника; – ускорение свободного падения.

Общее решение этого дифференциального уравнения имеет вид

, (4.11) где 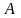и – постоянные, определяемые начальными условиями возбуждения колебаний.

Таким образом, при малых колебаниях математический маятник колеблется по гармоническому закону. Период колебаний математического маятника равен

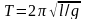. (4.12)

Видно, что период зависит только от длины маятника , ускорения силы тяжести и не зависит от его массы.

Физический маятник – любое тело, подвешенное в точке, лежащей вне его центра тяжести (рис 4.4).

Докажем, что маятник, отклоненный на малый угол  от положения равновесия, будет совершать гармонические колебания. Обозначим через I момент инерции маятника относительно оси О, перпендикулярной плоскости чертежа (рис.4.4). Пусть точка С является центром тяжести. Силу тяжести P = mg можно разложить на две составляющие, одна из которых P₂ уравновешивается реакцией опоры.

Под действием другой составляющей

P₁ = Psin = mg sin α (4.13)

маятник приходит в движение. Из основного закона динамики вращательного движения имеем

I  = - m g l_c sin , (4.14)

где 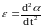, (4.15) угловое ускорение, l_c = СО – расстояние от точки подвеса до центра тяжести.

Знак минус выбран потому, что действующая сила направлена в сторону, противоположную положительному направлению отклонения маятника, т.е. стремится вернуть его в положение равновесия. При малых отклонениях можно считать, что sin   , поэтому

Р₁  m g  . (4.16)

Подставив (4.15) и (4.16) в (4.14), получим

. (4.17)

Полученное дифференциальное уравнение является уравнением гармонического колебательного движения. Частота и период колебаний определяются из формул

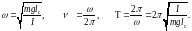(4.18)

Величина называется приведённой длиной физического маятника, она численно равна длине математического маятника с периодом колебаний, равным периоду колебаний данного физического маятника.

Таким образом, период и частота колебаний физического маятника определяются выражениями

. (4.19)