Решение

Предположим, что показатель преломления жидкости n_ж удовлет­воряет одному из двух неравенств:

n_ж < n₁< n₂; n₁ < п₂ < n_ж. (1)

Тогда для темных колец будет верна формула

.

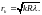Так как 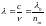, получим n_ж = kR₀ /r_k².

Выполнив вычисления, найдем:

1) n_ж1 = 1,41; 2) n_ж2 = 1,63.

Теперь пусть

n₁ < n_ж < n₂. (2)

В этом случае для темных колец верна формула

.

Тогда 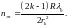Выполнив вычисления, получим: 1) n_ж1 = 1,34; 2) n_{ж 2} = 1,55.

Сравнив результаты вычислений для обоих случаев (очевидно, соответствующих двум разным жидкостям), видим, что в первом случае (n_ж1 = 1,41; n_ж1 = 1,34) значения по­казателя преломления жидкости удовлетворяют одному из неравенств (1), но не удовлетворяют неравенству (2). Следовательно, для первой жидкости n_ж1 = 1,41. Во втором случае (n_ж2 = 1,63; n_ж2 = 1,55) выполняется только неравен- ство (2). Следовательно, для второй жидкости n_ж2 = 1,55.

Пример 5. На щель шириной а =0,1мм падает нормально монохроматический свет с длиной волны λ = 500 нм. Дифракционная картина проецируется на экран, параллельный плоскости щели, с помощью линзы, расположенной вблизи щели. Определить расстояние L от экрана Э до линзы, если расстояние l между первыми дифракционными минимумами, расположенными по обе стороны центрального максимума, равно 1 см.

Решение

Условие дифракционных минимумов от одной щели, на которую свет падает нормально

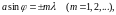(1)

где по условию задачи, m = 1.

Из рисунка следует, что l =2Ltgφ, но так как l/2 << L, то tg φ = sin φ, откуда sin φ = l/2L.

Подставив эти значения в формулу (1), получим искомое расстояние от экрана до линзы:

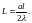
Вычисляя, получим L = 1м.

Пример 6. На дифракционную решетку нормально падает параллельный пучок лучей с длиной волны λ = 0,5 мкм. На экра­не, параллельном дифракционной решетке и отстоя- щем от нее на расстоянии L = 1 м, получается дифракционная картина. Расстояние между максимумами первого порядка, наблюдае­мыми на экране, оказалось равным r = 20,2 см.

Определить:

а) постоянную дифракционной решетки;

б) число штрихов на 1 см;

в) сколько максимумов дает при этом дифракционная решетка?

г) максимальный угол отклонения лучей, соответствую- щих последнему дифракционному максимуму.

Решение

а) Постоянная дифракционной решетки (а + b), длина волны λ и угол отклонения лучей φ, соответ­ствующий k-тому дифракционному максимуму, связаны соотно­шением

(a + b) sinφ = kλ, (1)

где k — порядок спектра. В данном случае k = 1, а

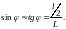
Указанное приближенное равенство имеет место, поскольку 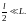Тогда соотношение (1) принимает вид

и 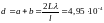см.

б) Число делений на 1 см найдем из формулы

см^-1.

в) Для определения числа максимумов, даваемых дифрак­ционной решеткой, вычислим сначала максимальное значение k, которое определяется из условия, что максимальный угол от­клонения лучей дифракционной решеткой не может превы­шать 90°. Из формулы (1)

найдем искомое значение k_mах. Подставляя sin = 1, получим k_max = 9,9.

Но так как k обязательно должно быть целым числом, то, следовательно, k_max = 9 (k не может принять значение, равное 10, так как при этом sin φ > 1).

Подсчитываем число максимумов, даваемых дифракционной решеткой: влево и вправо от центрального максимума будет наблюдаться одинаковое число максимумов, равное k_max, т. е. всего 2 k_max. Учитывая центральный (нулевой) максимум, полу­чим общее число максимумов

M = 2 k_max + 1= 19 максимумов.

г) Максимальный угол отклонения лучей, соответствую- щих последнему дифракционному максимуму, найдем, подставляя в формулу дифракционной решетки значение k = k_max

откуда находим искомое значение угла φ = 65°22'.

Пример 7. Определить длину волны монохрома- тического све­та, падающего нормально на дифракционную решетку с периодом d = 2,20 мкм, если угол между максимумами первого и второго порядков спектра Δφ = 15°.

Решение

Пусть φ₁, φ₂ - углы дифракции, соответствующие максимумам первого (k = 1) и второго (k = 2) порядков. По уcловию

φ₂ - φ₁ = Δφ. (1)

Из формулы дифракционной решетки следует

d sin φ₁ = λ, (2)

d sin φ₂ = 2 λ. (3)

Система уравнений (1), (2), (3) содержит три неизвестных: φ₁, φ₂, λ. Разделив почленно (2), (3), получим sin φ₂ = 2 sin φ₁, или, учи­тывая (1),

sin (φ₁ + Δφ) = 2 sin φ₁.

Решив это тригонометрическое уравнение относительно sin φ₁, найдем

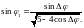(4)

Теперь из (2) с учетом (4) определим искомую величину:

мкм.

Пример 8. При каком минимальном числе штрихов дифрак­ционной решетки с периодом d = 2,9 мкм можно раз­решить компоненты дублета желтой линии натрия (λ₁= 5890 и λ₂ = 5896 )?